- 2021-04-27 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海市奉贤区中考数学一模试卷
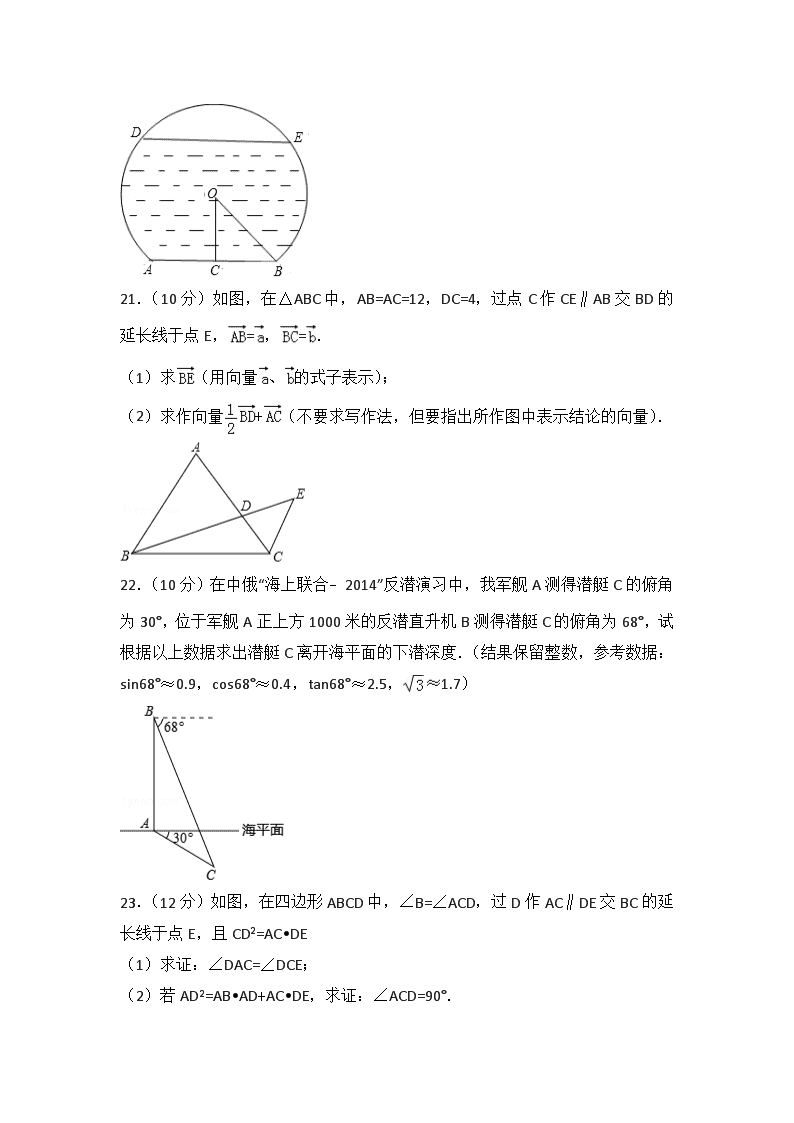
2015年上海市奉贤区中考数学一模试卷 一、选择题:(本大题共6题,每题4分,满分24分)[每小题只有一个正确选项,在答题纸的相应题号的选项上用2B铅笔填涂] 1.(4分)已知3x=2y,那么下列等式一定成立的是( ) A.x=2,y=3 B.= C.= D.3x+2y=0 2.(4分)在Rt△ABC中,∠ACB=90°,BC=1,AC=2,则下列结论正确的是( ) A.sinA= B.tanA= C.cosB= D.tanB= 3.(4分)抛物线y=﹣x2的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为( ) A.(0,﹣2) B.(0,2) C.(﹣2,0) D.(2,0) 4.(4分)在直角坐标平面中,M(2,0),圆M的半径为4,那么点P(﹣2,3)与圆M的位置关系是( ) A.点P在圆内 B.点P在圆上 C.点P在圆外 D.不能确定 5.(4分)一斜坡长为米,高度为1米,那么坡比为( ) A.1:3 B.1: C.1: D.1: 6.(4分)在同圆或等圆中,下列说法错误的是( ) A.相等弦所对的弧相等 B.相等弦所对的圆心角相等 C.相等圆心角所对的弧相等 D.相等圆心角所对的弦相等 二、填空题:(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置】 7.(4分)若与方向相反且长度为3,那么= . 8.(4分)若α为锐角,已知cosα=,那么tanα= . 9.(4分)△ABC中,∠C=90°,G为其重心,若CG=2,那么AB= . 10.(4分)一个矩形的周长为16,设其一边的长为x,面积为S,则S关于x的函数解析式是 . 11.(4分)如果抛物线y=x2+mx﹣1的顶点横坐标为1,那么m的值为 . 12.(4分)正n边形的边长与半径的夹角为75°,那么n= . 13.(4分)相邻两边长的比值是黄金分割数的矩形,叫做黄金矩形,从外形看,它最具美感.现在想要制作一张“黄金矩形”的贺年卡,如果较长的一条边长等于20厘米,那么相邻一条边的边长等于 厘米. 14.(4分)已知抛物线经过点(5,﹣3),其对称轴为直线x=4,则抛物线一定经过另一点的坐标是 . 15.(4分)如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,若△PEF的面积为3,那么△PDC与△PAB的面积和等于 . 16.(4分)已知圆A与圆B内切,AB=10,圆A半径为4,那么圆B的半径为 . 17.(4分)已知抛物线y=a(x+1)2+2过(0,y1)、(3,y2),若y1>y2,那么a的取值范围是 . 18.(4分)已知在△ABC中,∠C=90°,AC=3,BC=4.在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,若旋转后点C的对应点C′和点A、点B正好在同一直线上,那么∠A′AC′的正切值等于 . 三、解答题:(本大题共7题,满分78分) 19.(10分)计算:﹣cos60°. 20.(10分)一个弓形桥洞截面示意图如图所示,圆心为O,弦AB是水底线,OC⊥AB,AB=24m,sin∠COB=,DE是水位线,DE∥AB. (1)当水位线DE=4m时,求此时的水深; (2)若水位线以一定的速度下降,当水深8m时,求此时∠ACD的余切值. 21.(10分)如图,在△ABC中,AB=AC=12,DC=4,过点C作CE∥AB交BD的延长线于点E,=,=. (1)求(用向量、的式子表示); (2)求作向量+(不要求写作法,但要指出所作图中表示结论的向量). 22.(10分)在中俄“海上联合﹣2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,1.7) 23.(12分)如图,在四边形ABCD中,∠B=∠ACD,过D作AC∥DE交BC的延长线于点E,且CD2=AC•DE (1)求证:∠DAC=∠DCE; (2)若AD2=AB•AD+AC•DE,求证:∠ACD=90°. 24.(12分)已知抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线x=,D为OC中点,直线y=﹣2x+2与x轴交于点A,与y轴交于点D. (1)求此抛物线解析式和顶点P坐标; (2)求证:∠ODB=∠OAD; (3)设直线AD与抛物线的对称轴交于点M,点N在x轴上,若△AMP与△BND相似,求点N坐标. 25.(14分)已知:矩形ABCD中,过点B作 BG⊥AC交AC于点E,分别交射线AD于F点、交射线CD于G点,BC=6. (1)当点F为AD中点时,求AB的长; (2)联结AG,设AB=x,S△AFG=y,求y关于x的函数关系式及自变量x的取值范围; (3)是否存在x的值,使以D为圆心的圆与BC、BG都相切?若存在,求出x的值;若不存在,请说明理由. 2015年上海市奉贤区中考数学一模试卷 参考答案 一、选择题:(本大题共6题,每题4分,满分24分)[每小题只有一个正确选项,在答题纸的相应题号的选项上用2B铅笔填涂] 1.A;2.B;3.D;4.C;5.A;6.A; 二、填空题:(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置】 7.﹣3;8.;9.6;10.8x﹣x2;11.﹣2;12.12;13.(10﹣10);14.(3,﹣3);15.12;16.14;17.a<0;18.或3; 三、解答题:(本大题共7题,满分78分) 19.;20.;21.;22.;23.;24.;25.; 查看更多