数学华东师大版九年级上册教案24-4 解直角三角形 第2课时

数学华东师大版九年级上册教案24-4 解直角三角形 第2课时

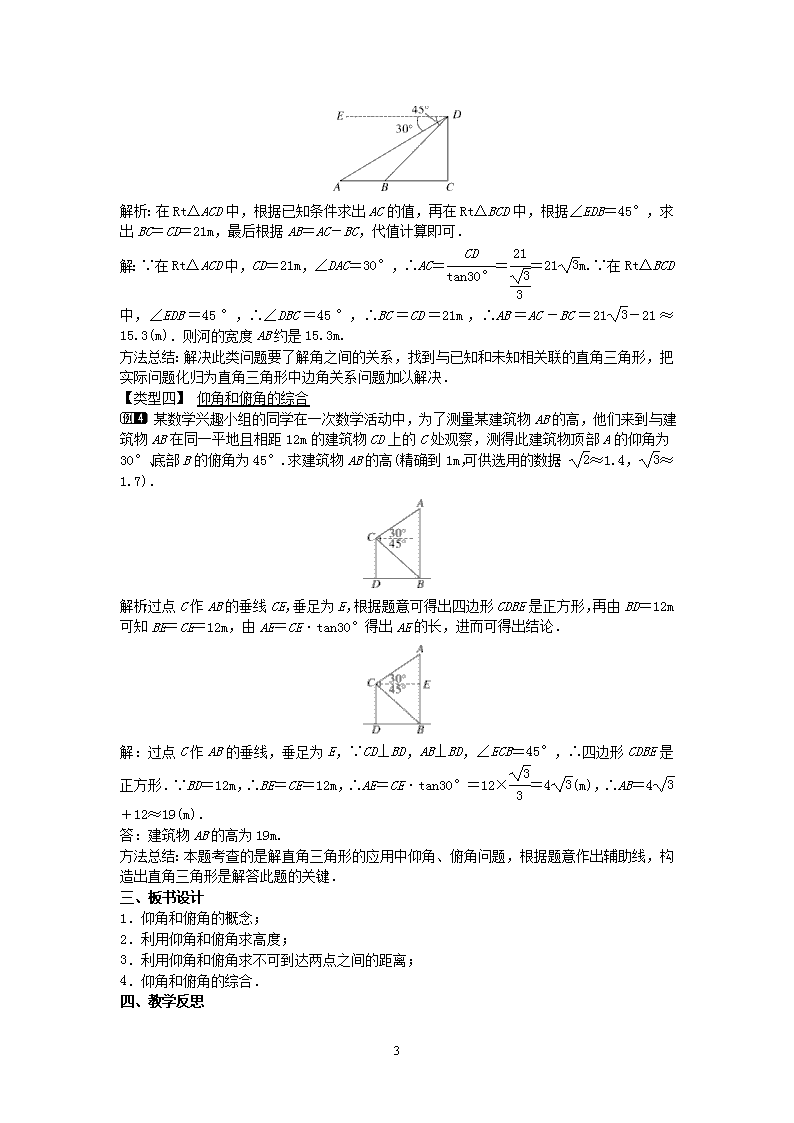
1 24.4 解直角三角形 第 2 课时 教学目标 1．使学生掌握仰角、俯角的意义，并学会正确地判断； 2．初步掌握将实际问题转化为解直角三角形问题的能力． 教学重难点 【教学重点】 仰角、俯角的意义. 【教学难点】 将实际问题转化为解直角三角形问题. 课前准备 无 教学过程 一、情境导入 在实际生活中，解直角三角形有着广泛的应用，例如我们通常遇到的视线、水平线、铅垂线 就构成了直角三角形．当我们测量时，在视线与水平线所成的角中，视线在水平线上方的角 叫做仰角，在水平线下方的角叫做俯角．今天我们就学习和仰角、俯角有关的应用性问题． 二、合作探究 探究点：利用仰(俯)角解决实际问题 【类型一】 利用仰角求高度 星期天，身高均为 1.6 米的小红、小涛来到一个公园，用他们所学的知识测算一座塔 的高度．如图，小红站在 A 处测得她看塔顶 C 的仰角α为 45°，小涛站在 B 处测得塔顶 C 的仰角β为 30°，他们又测出 A、B 两点的距离为 41.5m，假设他们的眼睛离头顶都是 10cm， 求塔高(结果保留根号)． 解析：设塔高为 xm，利用锐角三角函数关系得出 PM 的长，再利用CP PN ＝tan30°，求出 x 的 值即可． 2 解：设塔底面中心为 O，塔高 xm，MN∥AB 与塔中轴线相交于点 P，得到△CPM、△CPN 是直 角三角形，则x－（1.6－0.1） PM ＝tan45°，∵tan45°＝1，∴PM＝CP＝x－1.5.在 Rt△CPN 中，CP PN ＝tan30°，即 x－1.5 x－1.5＋41.5 ＝ 3 3 ，解得 x＝83 3＋89 4 . 答：塔高为 83 3＋89 4 m. 方法总结：解决此类问题要了解角与角之间的关系，找到与已知和未知相关联的直角三角 形．当图形中没有直角三角形时，要通过作高或垂线构造直角三角形． 【类型二】 利用俯角求高度 如图，在两建筑物之间有一旗杆 EG，高 15 米，从 A 点经过旗杆顶部 E 点恰好看到矮 建筑物的墙角 C 点，且俯角α为 60°，又从 A 点测得 D 点的俯角β为 30°.若旗杆底部 G 点为 BC 的中点，求矮建筑物的高 CD. 解析：根据点 G 是 BC 的中点，可判断 EG 是△ABC 的中位线，求出 AB.在 Rt△ABC 和 Rt△AFD 中，利用特殊角的三角函数值分别求出 BC、DF，继而可求出 CD 的长度． 解：过点 D 作 DF⊥AF 于点 F，∵点 G 是 BC 的中点，EG∥AB，∴EG 是△ABC 的中位线，∴AB ＝2EG＝30m.在 Rt△ABC 中，∵∠CAB＝30°，∴BC＝ABtan∠BAC＝30× 3 3 ＝10 3m.在 Rt△ AFD 中，∵AF＝BC＝10 3m，∴FD＝AF·tanβ＝10 3× 3 3 ＝10m，∴CD＝AB－FD＝30－10 ＝20m. 答：矮建筑物的高为 20m. 方法总结：本题考查了利用俯角求高度，解答本题的关键是构造直角三角形，利用三角函数 的知识求解相关线段的长度． 【类型三】 利用俯角求不可到达的两点之间的距离 如图，为了测量河的宽度 AB，测量人员在高 21m 的建筑物 CD 的顶端 D 处测得河岸 B 处的俯角为 45°，测得河对岸 A 处的俯角为 30°(A、B、C 在同一条直线上)，则河的宽度 AB 约是多少 m(精确到 0.1m，参考数据： 2≈1.41， 3≈1.73)? 3 解析：在 Rt△ACD 中，根据已知条件求出 AC 的值，再在 Rt△BCD 中，根据∠EDB＝45°，求 出 BC＝CD＝21m，最后根据 AB＝AC－BC，代值计算即可． 解：∵在 Rt△ACD 中，CD＝21m，∠DAC＝30°，∴AC＝ CD tan30° ＝ 21 3 3 ＝21 3m.∵在 Rt△BCD 中，∠EDB＝45°，∴∠DBC＝45°，∴BC＝CD＝21m，∴AB＝AC－BC＝21 3－21≈15.3(m)．则 河的宽度 AB 约是 15.3m. 方法总结：解决此类问题要了解角之间的关系，找到与已知和未知相关联的直角三角形，把 实际问题化归为直角三角形中边角关系问题加以解决． 【类型四】 仰角和俯角的综合 某数学兴趣小组的同学在一次数学活动中，为了测量某建筑物 AB 的高，他们来到与建 筑物 AB 在同一平地且相距 12m 的建筑物 CD 上的 C 处观察，测得此建筑物顶部 A 的仰角为 30°、底部 B 的俯角为 45°.求建筑物 AB 的高(精确到 1m，可供选用的数据： 2≈1.4， 3 ≈1.7)． 解析：过点 C 作 AB 的垂线 CE，垂足为 E，根据题意可得出四边形 CDBE 是正方形，再由 BD ＝12m 可知 BE＝CE＝12m，由 AE＝CE·tan30°得出 AE 的长，进而可得出结论． 解：过点 C 作 AB 的垂线，垂足为 E，∵CD⊥BD，AB⊥BD，∠ECB＝45°，∴四边形 CDBE 是 正方形．∵BD＝12m，∴BE＝CE＝12m，∴AE＝CE·tan30°＝12× 3 3 ＝4 3(m)，∴AB＝4 3 ＋12≈19(m)． 答：建筑物 AB 的高为 19m. 方法总结：本题考查的是解直角三角形的应用中仰角、俯角问题，根据题意作出辅助线，构 造出直角三角形是解答此题的关键． 三、板书设计 1．仰角和俯角的概念； 2．利用仰角和俯角求高度； 3．利用仰角和俯角求不可到达两点之间的距离； 4．仰角和俯角的综合． 四、教学反思 4 备课时尽可能站在学生的角度上思考问题，设计好教学过程中的每一个细节．上课前多 揣摩，让学生更多地参与到课堂的教学过程中，让学生体验思考的过程，体验成功的喜悦和 失败的挫折，舍得把课堂让给学生，让学生做课堂这个小小舞台的主角．使课堂更加鲜活， 充满人性魅力，下课后多反思，做好反馈工作，不断总结得失，不断进步．只有这样，才能 真正提高课堂教学效率.