《课堂设计》人教版八年级数学（上册）第十四章 14

《课堂设计》人教版八年级数学（上册）第十四章 14

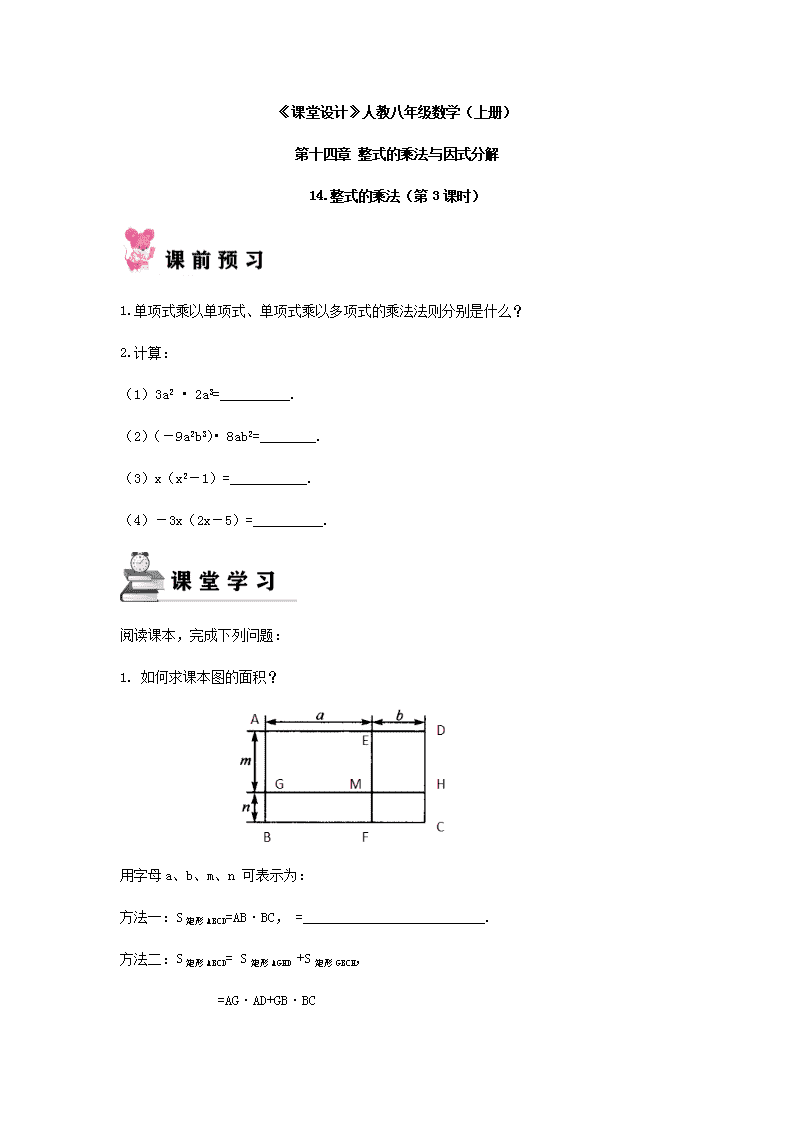
‎《课堂设计》人教八年级数学（上册）‎ 第十四章 整式的乘法与因式分解 ‎14.整式的乘法（第3课时）‎ ‎1.单项式乘以单项式、单项式乘以多项式的乘法法则分别是什么？‎ ‎2.计算：‎ ‎（1）3a2 • 2a3=__________. ‎ ‎（2）（－9a2b3）• 8ab2=________.‎ ‎（3）x（x2－1）=___________.‎ ‎（4）－3x（2x－5）=__________.‎ 阅读课本，完成下列问题：‎ 1. 如何求课本图的面积？‎ ‎ ‎ 用字母a、b、m、n 可表示为：‎ 方法一：S矩形ABCD=AB·BC， =__________________________.‎ 方法二：S矩形ABCD= S矩形AGHD +S矩形GBCH，‎ ‎=AG·AD+GB·BC ‎=______________________________.‎ 方法三：（你还有什么方法？）‎ S矩形ABCD=‎ ‎2.利用以上结论可知：‎ ‎(a+b)(m+n)=a( )+b( )‎ ‎=___________________.‎ ‎3. 多项式与多项式相乘的法则：‎ 多项式与多项式相乘，先用一个多项式的______________乘另一个多项式的___________，再把所得的积________．‎ ‎4.阅读课本例题6，并思考：‎ ①例题中的符号是怎样处理的？‎ ②需要注意什么问题？‎ ‎1.判断题：‎ ‎①(x+2)(x+3)=x2+6；( )‎ ‎②(x-1)(x+2)=x2-2；( )‎ ③(x-1)(x-5)=x2+5x-5；( )‎ ‎2.计算：‎ ‎①(2x+2)(x+3)‎ ‎②(x2-1)(x+2)‎ ③(x-y)(x-3y)‎ ④（2x＋5y）（3x－2y）‎ ⑤(x-y)(x2+xy+y)‎ ‎1.填空题：‎ ‎(1)(x2+3)(3x2-1)＝ ；‎ ‎(2)(-a+3b2)(a2-4b)＝ ；‎ ‎(3)(b+c)(a+b)(c+a)＝ ；‎ ‎(4)x(4-2x)(3-2x)＝ ；‎ ‎(5)(x+1)2= .‎ ‎2.选择题 ‎(1)多项式2a-3b与多项式a+5b的积是( ).‎ A.2a2+7ab B.2a2+7ab-15b2 C.2a2+10ab-15b2 D.2a2-3ab-15b2‎ ‎(2)计算(-)(+)+b2的结果是( ).‎ A.a2 B.(a2+5b2) C.(a2-5b2) D.a2+b2‎ ‎(3)方程(2x+3)(x-4)-(x+2)(x-3)=x2+6的解是( ).‎ A.x=4 B.x=-4 C.x=3 D.x=-3‎ ‎(4)在计算:‎ ‎①(m-2n)(3m+n)＝3m2-5mn-2n2,‎ ‎②(1+2x)(1-2x)＝1-4x+4x2,‎ ‎③(2a-3b)(2a-5b)＝4a2-16ab+15b2,‎ ‎④(x+2y)(3x+6y)＝3x2+6xy+12y2中，正确的有( )‎ A.1个 B.2个 C.3个 D.4个 ‎3.计算或化简:‎ ‎（1）5x(x+2)2-x(x-3)(5x+4)‎ ‎ ‎ ‎（2）(0.2a-1.5b)(0.4a-4b)‎ ‎ ‎ ‎（3）(x+2y)(x-2y)-(2x+y)(x-2y).‎ ‎ ‎ ‎4. 先化简，再求值.‎ ‎ (1)(x+1)(x+2)(2x-1)-(x2-2x+1)，其中x=-1.‎ ‎ ‎ ‎(2) 已知x2-2x=2，将下式化简，再求值：(x-1)2+(x+3)(x-3)+(x-3)(x-1).‎ 参考答案 课堂检测 ‎1.× × × ‎ ‎2. ①2x2+8x+6 ②x3+2x2-x-2 ③x2-4xy+3y ④6x2+11xy-10y2 ⑤x3-y3 ‎ 课后提高 ‎1.(1)3x4+8x2-3;‎ ‎(2)-a3+3a2b2+2ab-12b3;‎ ‎(3)2abc+a2b+ac2+a2c+b2c+b2a;‎ ‎(4)12x-14x2+4x4;(5)x2+2x+1.‎ ‎2.B D C B ‎3.(1)32x+31x3 (2)0.08a2-1.4ab+6b2 ‎ ‎(3)-x2-2y2+3xy ‎ ‎4.-4 1 ‎