数学文卷·2018届河北省涞水波峰中学高二下学期期中考试（2017-04）

数学文卷·2018届河北省涞水波峰中学高二下学期期中考试（2017-04）

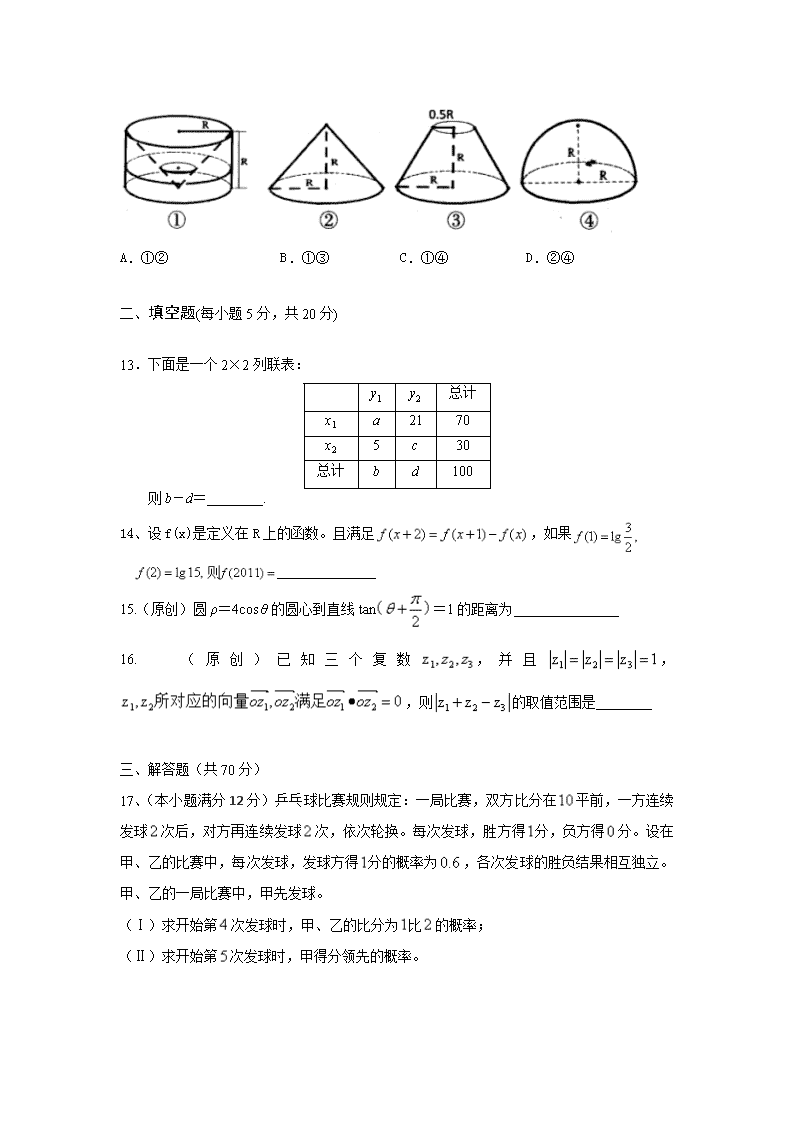
学校 姓名 班级 考场 考号 ‎ ‎ 密 封 线 内 不 要 答 题 密 封 线 波峰中学2016-2017学年度第二学期期中考试 高二数学文科试题 一、 选择题(每小题5分，共60分)‎ ‎1. (原创）已知复数（为虚数单位），则的共轭复数是 （ ） A. B. C. D. ‎ ‎2、已知回归直线的斜率的估计值是1.23，样本点的中心为(4，5)，则回归直线的方程是( )‎ ‎ A.=1.23x＋4 B. =1.23x+5 C. =1.23x+0.08 D. =0.08x+1.23‎ ‎3、有一段演绎推理是这样的“有些有理数是真分数，整数是有理数，则整数是真分数”结论显然是错误的，是因为（ ）‎ A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误 ‎4、在下列表格中,每格填上一个数字后,使每一行成等差数列,每一列成等比数列,则a+b+c的值是( ) A. 1 B. 2 C. 3 D. 4‎ ‎1‎ ‎2‎ ‎0.5‎ ‎1‎ a b c ‎5.（原创）已知点M在角q终边的延长线上，且,则M的坐标为（ ）‎ ‎ A. B. ‎ ‎ C. D.‎ ‎6.如图，5个(x，y)数据，去掉D(3,10)后，下列说法错误的是( )‎ ‎ A．相关系数r变大 B．残差平方和变大 ‎ C．R2变大 D．解释变量x与预报变量y的相关性变强 ‎ ‎ ‎7．独立性检验中，假设H0：变量X与变量Y没有关系，则在H0成立的情况下，P(K2≥6.635)≈0.010表示的意义是(　　)‎ A．变量X与变量Y有关系的概率为1%‎ B．变量X与变量Y有关系的概率为99.9%‎ C．变量X与变量Y没有关系的概率为99%‎ D．变量X与变量Y有关系的概率为99%‎ ‎8．下表为某班5位同学身高（单位：cm）与体重（单位kg）的数据，‎ 身高 ‎170‎ ‎171‎ ‎166‎ ‎178‎ ‎160‎ 体重 ‎75‎ ‎80‎ ‎70‎ ‎85‎ ‎65‎ 若两个量间的回归直线方程为，则的值为（ ）‎ A．121.04 B．123.2 C．21 D．45.12‎ ‎9．用反证法证明命题：“，，，且，则 中至少有一个负数”时的假设为（ ）‎ A．中至少有一个正数 B．全为正数 C．全都大于等于0 D．中至多有一个负数 ‎10.曲线(θ为参数)的对称中心(　 )‎ A.在直线y＝2x上 B.在直线y＝－2x上 C.在直线y＝x－1上 D.在直线y＝x＋1上 ‎11、欧拉公式(为虚数单位)是由瑞士著名数学家欧拉发明的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”．在复平面中表示的复数位于（ ）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎12.祖暅是南北朝时代的伟大科学家，5世纪末提出体积计算原理，即祖暅原理：“幂势既同，则积不容异”．意思是：夹在两个平行平面之间的两个几何体，被平行于这两个平面的任何一个平面所截，如果截面面积都相等，那么这两个几何体的体积一定相等．现有以下四个几何体：图①是从圆柱中挖出一个圆锥所得的几何体；图②、图③、图④分别是圆锥、圆台和半球，则满足祖暅原理的两个几何体为（　　）‎ A．①② B．①③ C．①④ D．②④ ‎ 一、 填空题(每小题5分，共20分)‎ ‎13．下面是一个2×2列联表：‎ y1‎ y2‎ 总计 x1‎ a ‎21‎ ‎70‎ x2‎ ‎5‎ c ‎30‎ 总计 b d ‎100‎ ‎ 则b－d＝________.‎ ‎14、设f(x)是定义在R上的函数。且满足，如果 ‎ ‎15.（原创）圆ρ＝4cos θ的圆心到直线tan＝1的距离为 ‎ ‎16.（原创）已知三个复数，并且，，则的取值范围是 ‎ 三、解答题（共70分）‎ ‎17、（本小题满分12分）乒乓球比赛规则规定：一局比赛，双方比分在平前，一方连续发球次后，对方再连续发球次，依次轮换。每次发球，胜方得分，负方得分。设在甲、乙的比赛中，每次发球，发球方得分的概率为，各次发球的胜负结果相互独立。甲、乙的一局比赛中，甲先发球。‎ ‎（Ⅰ）求开始第次发球时，甲、乙的比分为比的概率；‎ ‎（Ⅱ）求开始第次发球时，甲得分领先的概率。‎ ‎18、（本小题满分12分）某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费错误！未找到引用源。和年销售量错误！未找到引用源。（i=1,2，···，8）数据作了初步处理，得到下面的散点图及一些统计量的值。‎ ‎46.6‎ ‎563‎ ‎6.8‎ ‎289.8‎ ‎1.6‎ ‎1469‎ ‎108.8‎ 表中w1 =1, ， =1‎ ‎（Ⅰ）根据散点图判断，y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）‎ ‎（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；‎ ‎（Ⅲ）以知这种产品的年利率z与x、y的关系为z=0.2y-x。根据（Ⅱ）的结果回答下列问题：‎ ‎（1）年宣传费x=49时，年销售量及年利润的预报值是多少？‎ ‎（2）年宣传费x为何值时，年利率的预报值最大？‎ 附：对于一组数据（u1 v1）,（u2 v2）…….. （un vn）,其回归线的斜率和截距的最小二乘估计分别为：‎ ‎19、（本小题满分12分）某公司计划购买1台机器，该种机器使用三年后即被淘汰.机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元.在机器使用期间，如果备件不足再购买，则每个500元.现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：‎ ‎ ‎ 记x表示1台机器在三年使用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用（单位：元），n表示购机的同时购买的易损零件数.‎ ‎（I）若n=19，求y与x的函数解析式；‎ ‎（II）若要求“需更换的易损零件数不大于n”的频率不小于0.5，求n的最小值；‎ ‎（III）假设这100台机器在购机的同时每台都购买19个易损零件，或每台都购买20个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买19个还是20个易损零件？‎ ‎20、（本小题满分12分）教育学家分析发现加强语文阅读理解训练与提高数学应用题得分率有关，某校兴趣小组为了验证这个结论，从该校选择甲、乙两个同轨班级进行试验，其中甲班加强阅读理解训练，乙班常规教学无额外训练，一段时间后进行数学应用题测试，统计数据情况如下面2*2列联表：（单位：人）‎ 优秀人数 非优秀人数 总计 甲班 ‎22‎ ‎8‎ ‎30‎ 乙班 ‎8‎ ‎12‎ ‎20‎ 总计 ‎30‎ ‎20‎ ‎50‎ ‎（1）能否据此判断有97.5％的把握认为加强语文阅读理解训练与提高数学应用题得分率有关；‎ ‎（2）经过多次测试后，小明正确解答一道数学应用题所用的时间在5-7分钟，小刚正确解答一道数学应用题所用的时间在6-8分钟，现小明丶小刚同时独立解答同一道数学应用题，求小刚比小明先正确解答完的概率。‎ ‎ 附表及公式：‎ P（）‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎21、（本小题满分10分）选修4—4：坐标系与参数方程 在直角坐标系xoy中，曲线C1的参数方程为（t为参数，a＞0）．在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C2：‎ ‎（I）说明C1是哪一种曲线，并将C1的方程化为极坐标方程； ‎ ‎（II）直线C3的极坐标方程为，其中满足，若曲线C1与C2的公共点都在C3上，求a．‎ ‎22、（本小题满分10分）选修4-4；坐标系与参数方程 ‎ 在直角坐标系中，直线:x=,圆：，以坐标原点为极点，轴的正半轴为极轴建立极坐标系。‎ ‎（1）求，C2的极坐标方程。‎ ‎（2）若直线C3的极坐标为=（ρR）,设C2与C3的交点为M，N,求△C2MN的面积 ‎1-5BCCAC 6-10BDACB 11-12BC ‎13.8 14. 15. 16. ‎ ‎17（本小题满分12分）‎ 乒乓球比赛规则规定：一局比赛，双方比分在平前，一方连续发球次后，对方再连续发球次，依次轮换。每次发球，胜方得分，负方得分。设在甲、乙的比赛中，每次发球，发球方得分的概率为，各次发球的胜负结果相互独立。甲、乙的一局比赛中，甲先发球。‎ ‎（Ⅰ）求开始第次发球时，甲、乙的比分为比的概率；‎ ‎（Ⅱ）求开始第次发球时，甲得分领先的概率。‎ 答案：（Ⅰ）开始第次发球时,甲、乙的比分为比的情况包括：甲乙乙，乙甲乙，乙乙甲三种 则开始第次发球时，甲、乙的比分为比的概率 ‎（Ⅱ）开始第次发球时，甲得分领先的情况包括:甲甲甲甲，甲甲甲乙，甲甲乙甲，甲乙甲甲，乙甲甲甲，‎ 则开始第次发球时，甲得分领先的概率 ‎（18）（本小题满分12分）某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费错误！未找到引用源。和年销售量错误！未找到引用源。（i=1,2，···，8）数据作了初步处理，得到下面的散点图及一些统计量的值。‎ ‎46.6‎ ‎563‎ ‎6.8‎ ‎289.8‎ ‎1.6‎ ‎1469‎ ‎108.8‎ 表中w1 =1, ， =1‎ （1） 根据散点图判断，y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）‎ ‎（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；‎ ‎（Ⅲ）以知这种产品的年利率z与x、y的关系为z=0.2y-x。根据（Ⅱ）的结果回答下列问题：‎ ‎(1)年宣传费x=49时，年销售量及年利润的预报值是多少？‎ ‎(2)年宣传费x为何值时，年利率的预报值最大？‎ 附：对于一组数据（u1 v1）,（u2 v2）…….. （un vn）,其回归线的斜率和截距的最小二乘估计分别为：‎ ‎【答案】（Ⅰ）适合作为年销售关于年宣传费用的回归方程类型（Ⅱ）（Ⅲ）46.24‎ ‎∴关于的回归方程为.……6分 考点：非线性拟合；线性回归方程求法；利用回归方程进行预报预测；应用意识 ‎（19）（本小题满分12分）某公司计划购买1台机器，该种机器使用三年后即被淘汰.机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元.在机器使用期间，如果备件不足再购买，则每个500元.现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：‎ ‎ ‎ 记x表示1台机器在三年使用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用（单位：元），表示购机的同时购买的易损零件数.‎ ‎（I）若=19，求y与x的函数解析式；‎ ‎（II）若要求“需更换的易损零件数不大于”的频率不小于0.5，求的最小值；‎ ‎（III）假设这100台机器在购机的同时每台都购买19个易损零件，或每台都购买20个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买19个还是20个易损零件？‎ ‎【答案】（I）；（II）19；（III）19.‎ ‎【解析】‎ ‎（Ⅱ）由柱状图知，需更换的零件数不大于18的频率为0.46，不大于19的频率为0.7，故的最小值为19.‎ ‎（Ⅲ）若每台机器在购机同时都购买19个易损零件，则这100台机器中有70台在购买易损零件上的费用为3800，20台的费用为4300，10台的费用为4800，因此这100台机器在购买易损零件上所需费用的平均数为.‎ 若每台机器在购机同时都购买20个易损零件，则这100台机器中有90台在购买易损零件上的费用为4000，10台的费用为4500，因此这100‎ 台机器在购买易损零件上所需费用的平均数为.‎ 比较两个平均数可知，购买1台机器的同时应购买19个易损零件.‎ 考点：函数解析式、概率与统计 ‎20、（本小题满分12分）教育学家分析发现加强语文阅读理解训练与提高数学应用题得分率有关，某校兴趣小组为了验证这个结论，从该校选择甲、乙两个同轨班级进行试验，其中甲班加强阅读理解训练，乙班常规教学无额外训练，一段时间后进行数学应用题测试，统计数据情况如下面2*2列联表：（单位：人）‎ 优秀人数 非优秀人数 总计 甲班 ‎22‎ ‎8‎ ‎30‎ 乙班 ‎8‎ ‎12‎ ‎20‎ 总计 ‎30‎ ‎20‎ ‎50‎ ‎（1）能否据此判断有97.5％的把握认为加强语文阅读理解训练与提高数学应用题得分率有关；‎ ‎（2）经过多次测试后，小明正确解答一道数学应用题所用的时间在5-7分钟，小刚正确解答一道数学应用题所用的时间在6-8分钟，现小明丶小刚同时独立解答同一道数学应用题，求小刚比小明先正确解答完的概率。‎ ‎ 附表及公式：‎ P（）‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 答案： （1）由表中数据得的观测值为 所以根据统计有97.5％的把握认为加强语文阅读理解训练与提高数学应用题得分率有关。‎ ‎(2) 设小明与小刚解答这道题的时间分别为x、y分钟，则基本事件满足的区域为 设事件Ａ为小刚比小明先正确解答完此题，则满足的区域为x>y X y O 所以由几何概型即小刚比小明先解答完此题的概率为.‎ ‎（21）（本小题满分10分）选修4—4：坐标系与参数方程 在直角坐标系xy中，曲线C1的参数方程为（t为参数，a＞0）．在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=.‎ ‎（I）说明C1是哪一种曲线，并将C1的方程化为极坐标方程；‎ ‎（II）直线C3的极坐标方程为，其中满足tan=2，若曲线C1与C2的公共点都在C3上，求a．‎ ‎【答案】（I）圆，；（II）1.‎ ‎【解析】‎ ‎ ‎ 考点：参数方程、极坐标方程与直角坐标方程的互化及应用 ‎（22）（本小题满分10分）选修4-4；坐标系与参数方程 ‎ 在直角坐标系中，直线:x=,圆：，以坐标原点为极点，轴的正半轴为极轴建立极坐标系。‎ ‎（1）求，C2的极坐标方程。‎ ‎（2）若直线C3的极坐标为=（ρR）,设C2与C3的交点为M，N,求△C2MN的面积 ‎【答案】（Ⅰ）,（Ⅱ）‎ ‎【解析】‎ 试题分析：（Ⅰ）用直角坐标方程与极坐标互化公式即可求得，的极坐标方程；（Ⅱ）将将代入即可求出|MN|，利用三角形面积公式即可求出的面积.‎ 试题解析：（Ⅰ）因为，‎ ‎∴的极坐标方程为，的极坐标方程为.……5分 ‎ （Ⅱ）将代入，得，解得=，=，|MN|=－=，‎ 因为的半径为1，则的面积=.‎ 考点：直角坐标方程与极坐标互化；直线与圆的位置关系 ‎【答案】（Ⅰ）,（Ⅱ）‎ ‎【解析】‎ 试题分析：（Ⅰ）用直角坐标方程与极坐标互化公式即可求得，的极坐标方程；（Ⅱ）将将代入即可求出|MN|，利用三角形面积公式即可求出的面积.‎ 试题解析：（Ⅰ）因为，‎ ‎∴的极坐标方程为，的极坐标方程为.……5分 ‎ （Ⅱ）将代入，得，解得=，=，|MN|=－=，‎ 因为的半径为1，则的面积=.‎ 考点：直角坐标方程与极坐标互化；直线与圆的位置关系