- 2021-04-25 发布 |
- 37.5 KB |
- 22页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版高中数学选修1-1课件:3_3_2《函数的极值与导数》
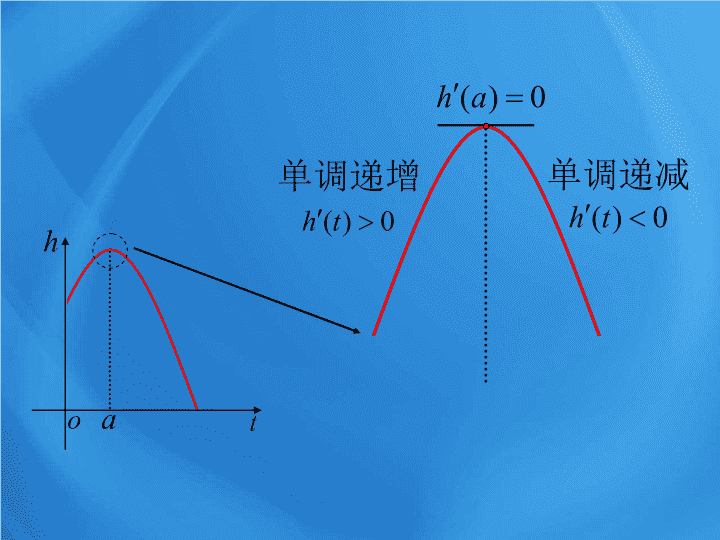
3.3.2 函数的极值与导数 第三章 导数及其应用 跳水运动中 , 运动员相对于水面的高度 h ( 单位:米 ) 与起跳后的时间 t ( 单位:秒 ) 存在函数关系 h ( t )=-4.9 t 2 +6.5 t +10 其图象如右 . 单调递增 单调递减 对于 d 点 函数 y = f ( x ) 在点 x = d 的函数值 f ( d ) 比在其附 近其他点的函数值都小, =0 。 在点 x = d 附近的左侧 <0 在点 x = d 附近的右侧 >0 我们把点 d 叫做函数 y = f ( x ) 的 极小值点 , f ( d ) 叫做函数 y = f ( x ) 的 极小值 。 在点 x = e 附近的左侧 >0 在点 x = e 附近的右侧 <0 对于 e 点 函数 y = f ( x ) 在点 x = e 的函数值 f ( e ) 比在其附 近其他点的函数值都大, =0 。 我们把点 e 叫做函数 y = f ( x ) 的 极大值点 , f ( e ) 叫做函数 y = f ( x ) 的 极大值 。 极小值点、极大值点统称为极值点 极小值、极大值统称为极值 极大值一定大于极小值吗? 不一定 例 1 、求函数 f ( x )= x 3 - 12 x +12 的极值。 解: =3 x 2 - 12=3( x - 2)( x +2) 令 =0 得 x =2, 或 x = - 2 下面分两种情况讨论: (1) 当 >0 即 x >2, 或 x < - 2 时 ; (2) 当 <0 即 - 2< x <2 时 ; x ( - ∞, - 2) - 2 ( - 2,2) 2 (2,+∞) + 0 - 0 + f ( x ) 单调递增↗ 28 单调递减↘ - 4 单调递增↗ 当 x 变化时, , f ( x ) 的变化情况如下表; 因此,当 x = - 2 时, f ( x ) 有极大值, 并且极大值为 f ( - 2)=28 当 x =2 时, f ( x ) 有极小值, 并且极小值为 f (2)= - 4 图象如右 练习 1 、求函数 f ( x )=6+12 x - x 3 =12 - 3 x 2 =3(4 - x 2 )=3(2 - x )(2+ x ) x ( - ∞, - 2) - 2 ( - 2,2) 2 (2,+∞) - 0 + 0 - f ( x ) ↘ - 10 ↗ 22 ↘ 一般地 , 求函数的极值的方法是 : 解方程 =0. 当 =0 时 . ① 如果在 x 0 附近的左侧 右侧 那么 , f(x 0 ) 是极大值 ; ② 如果在 x 0 附近的左侧 右侧 那么 , f(x 0 ) 是极小值 . 即“峰顶” 即“谷底” 例 2 、已知函数 f ( x )= ax 3 + bx 2 - 2 x 在 x = - 2, x =1 处取得极值: (1) 求函数的解析式; (2) 求函数 f ( x ) 的单调区间。 解: (1) =3 ax 2 +2 bx - 2 因为 f ( x ) 在 x = - 2, x =1 处取得极值,所以 解得 =3 ax 2 +2 bx - 2 即 f ( x )= ax 3 + bx 2 - 2 x = x 2 + x - 2 由 >0, 得 x < - 2 或 x >1, 所以 f ( x ) 的单调增区间为 ( - ∞, - 2) ∪(1,+∞) 由 <0, 得 - 2< x <1, 所以 f ( x ) 的单调减区间为 ( - 2,1) 导数值为 0 的点一定是函数的极值点吗? 思考 但 x =0 不是函数的极值点 导数为零的点是 该点为极值点的必要条件 , 而不是充分条件 . 小结 一般地 , 求函数的极值的方法是 : 解方程 =0. 当 =0 时 . ① 如果在 x 0 附近的左侧 右侧 那么 , f(x 0 ) 是极大值 ; ② 如果在 x 0 附近的左侧 右侧 那么 , f(x 0 ) 是极小值 . 即“峰顶” 即“谷底” 再见查看更多