高一物理《2-3-2-4匀变速直线运动的位移关系》教案（必修一）

高一物理《2-3-2-4匀变速直线运动的位移关系》教案（必修一）

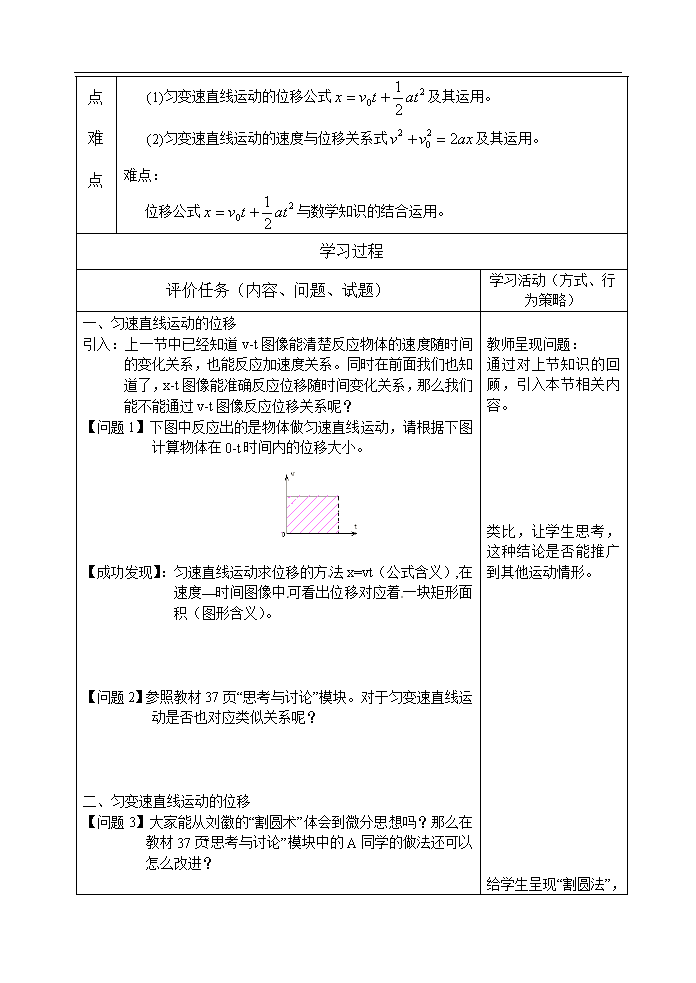
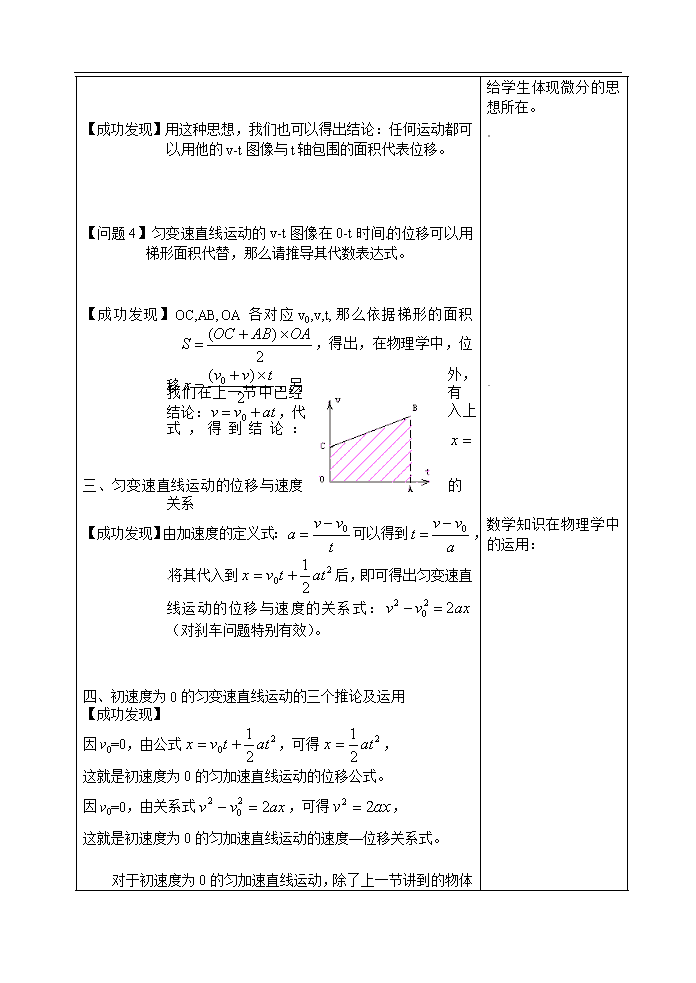
课 题 名 称 课 时 数 4 课 时 课 型 问题解决 课 课 程 标 准 《普通高中物理课程标准》中对本节知识的具体内容标准如下： 1.知道匀变速直线运动的位移与 v-t 图像的面积的对应关系； 2.理解匀变速直线运动的位移与 v-t 图像中矩形条面积的对应关系，让学生感受到 极限思维法在物理中的运用； 3.理解匀变速直线运动的位移与时间的关系。 4.理解匀变速直线运动的速度与位移的关系。 学 习 目 标 1．知识与技能： (1)了解位移公式的推导过程，掌握位移时间公式 2 0 2 1 attvx  及速度与位移 公式 axvv 22 0 2  ； (2)理解匀变速直线运动的位移与时间及速度与位移的关系及其应用； (3)理解 v-t 图线与时间轴所夹的面积表示物体在 t 时间内的位移 ； (4)会适当的运用公式对匀变速直线运动的问题进行简单的计算与分析； 2．过程与方法： (1)通过近似推导位移的公式的过程，体验数学微元法的特点和技巧，能把瞬时 速度的求法与此相对比； (2)感悟数学知识在物理学中的运用。 3．情感态度与价值观： 经历微元法推导位移公式，培养学生自己动手能力，增加物理情感。 重 重点： 点 难 点 (1)匀变速直线运动的位移公式 2 0 2 1 attvx  及其运用。 (2)匀变速直线运动的速度与位移关系式 axvv 22 0 2  及其运用。 难点： 位移公式 2 0 2 1 attvx  与数学知识的结合运用。 学习过程 评价任务（内容、问题、试题） 学习活动（方式、行 为策略） 一、匀速直线运动的位移 引入：上一节中已经知道 v-t 图像能清楚反应物体的速度随时间 的变化关系，也能反应加速度关系。同时在前面我们也知 道了，x-t 图像能准确反应位移随时间变化关系，那么我们 能不能通过 v-t 图像反应位移关系呢？ 【问题 1】下图中反应出的是物体做匀速直线运动，请根据下图 计算物体在 0-t 时间内的位移大小。 【成功发现】：匀速直线运动求位移的方 法 x=vt（公式含义）, 在速度—时间图像中 可看出位移对应着一块矩形 面积（图形含义）。 【问题 2】参照教材 37 页“思考与讨论”模块。对于匀变速直线运 动是否也对应类似关系呢？ 二、匀变速直线运动的位移 【问题 3】大家能从刘徽的“割圆术”体会到微分思想吗？那么在 教材 37 页“思考与讨论”模块中的 A 同学的做法还可以 怎么改进？ 教师呈现问题： 通过对上节知识的回 顾，引入本节相关内 容。 类比，让学生思考， 这种结论是否能推广 到其他运动情形。 给学生呈现“割圆法”， 【成功发现】用这种思想，我们也可以得出结论：任何运动都可 以用他的 v-t 图像与 t 轴包围的面积代表位移。 【问题 4】匀变速直线运动的 v-t 图像在 0-t 时间的位移可以用梯 形面积代替，那么请推导其代数表达式。 【成功发现】OC,AB,OA 各对应 v0,v,t,那么依据梯形的面积 2 )( OAABOCS  ，得出，在物理学中，位 移 2 )( 0 tvvx  ，另 外， 我们在上一节中已经 有 结论： atvv  0 ，代 入 上 式 ， 得 到 结 论 ： 2 0 2 1 attvx  三、匀变速直线运动的位移与速度的关系 【成功发现】由加速度的定义式： t vva 0 可以得到 a vvt 0 ， 将其代入到 2 0 2 1 attvx  后，即可得出匀变速直 线运动的位移与速度的关系式： axvv 22 0 2  （对 刹车问题特别有效）。 四、初速度为 0 的匀变速直线运动的三个推论及运用 【成功发现】 因 v0=0，由公式 2 0 2 1 attvx  ，可得 2 2 1 atx  ， 这就是初速度为 0 的匀加速直线运动的位移公式。 因 v0=0，由关系式 axvv 22 0 2  ，可得 axv 22  ， 这就是初速度为 0 的匀加速直线运动的速度—位移关系式。 对于初速度为 0 的匀加速直线运动，除了上一节讲到的物体 给学生体现微分的思 想所在。 数学知识在物理学中 的运用： [来源:学科网] 在时刻 t、2t、3t、…… n t 的速度之比 v1︰v2︰v3︰……︰vn=1︰2 ︰3︰……︰n 之外，还有如下的一些比例关系：因加速度 a 为定值，由 axv 22  ，可得 xv  。所以，在物体做初速度为 0 的匀加速 直线运动时，物体通过位移 x、2x、3x、…… nx 时的速度之比 v1’︰v2’︰v3’︰……︰vn’= 1 ︰ 2 ︰ 3 ︰……︰ n 。 因加速度 a 为定值，由 2 2 1 atx  可得 2tx  。所以，在物 体做初速度为 0 的匀加速直线运动时，物体在时间 t、2t、3t、…… nt 内通过的位移之比 x1︰x2︰x3︰……︰x n =12︰22︰32︰……︰ n2。 由上式可得 x1︰(x2－x1) ︰(x3－x2)︰……︰(x n－x n-1)=1︰3︰5 ︰……︰(2n－1)。这就是说，在物体做初速度为 0 的匀加速直线 运动时，从开始计时的连续相等的时间内，物体通过的位移之比 等于从 1 开始的连 续奇数比，即 xⅠ︰xⅡ︰xⅢ︰……︰xN= 1︰3︰5︰……︰(2n－1)。 因加速度 a 为定值，由 2 2 1 atx  可得 xt  。所以，在物体做 初速度为 0 的匀加速直线运动时，物体通过位移 x、2x、3x、…… nx 所需的时间之比 t1︰t2︰t3︰……︰t n = 1 ︰ 2 ︰ 3 ︰……︰ n 。 由上式可得 t1︰(t2－t1) ︰(t3－t2)︰……︰(t n－t n-1)= 1 ︰( 2 － 1 )︰( 3 － 2 )︰……︰( n － 1n )。这就是说，在物体 做初速度为 0 的匀加速直线运动时，从开始计时起，通过连续相 等的位移所需的时间之比 tⅠ︰tⅡ︰tⅢ︰……︰tN = 1 ︰( 2 － 1 )︰( 3 － 2 )︰……︰ ( n － 1n )。 【课堂精炼】 【例 1】在某次交通事故中，交警测量汽车刹车线的长，用以判 断该车是否超速。请问还需什么数据，如何计算？ [来源:学,科,网 Z,X,X,K] [来源:Zxxk.Com] [来源:学&科&网 Z&X&X&K] 【例 2】某航空母舰上飞机在跑道加速时，发动机最大加速度 5m/s2，所需起飞速度为 50m/s ，跑道长 100m，通过计算 判断，飞机能否靠自身发动机从舰上起飞？为了使飞机 在开始滑行时就有一定的初速度，航空母舰装有弹射装 置，对于该型号的舰载飞机，弹射系统必须使它具有多 大的初速度？ 精讲精练： 教师在学生完成过程 中巡视并观察，搜集 整 理 学 生 存 在 的 问 题。 课 后 反 思 [来源:Z#xx#k.Com]