高二物理同步训练：3

高二物理同步训练：3

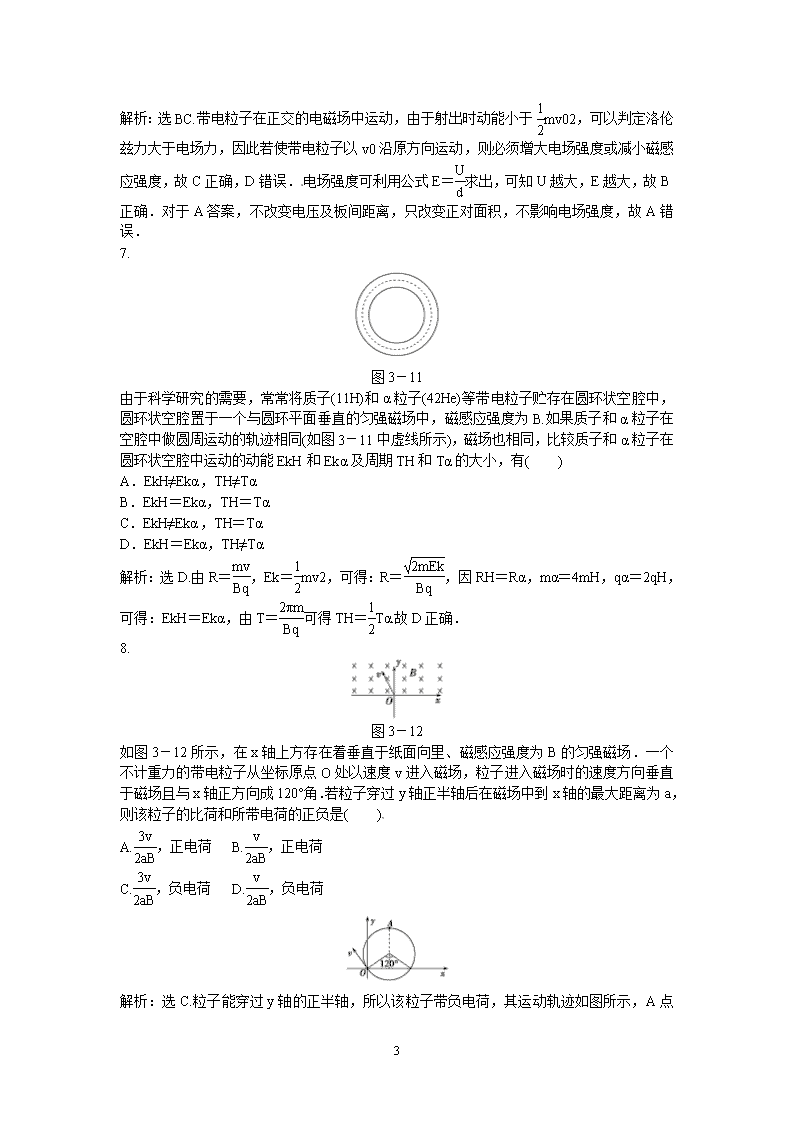
高二物理同步训练试题解析 ‎ 一、选择题 ‎1．有关洛伦兹力和安培力的描述，正确的是(　　)‎ A．通电直导线在匀强磁场中一定受到安培力的作用 B．安培力是大量运动电荷所受洛伦兹力的宏观表现 C．带电粒子在匀强磁场中运动受到的洛伦兹力做正功 D．通电直导线在磁场中受到的安培力方向与磁场方向平行 解析：选B.安培力方向与磁场垂直，洛伦兹力不做功，通电导线在磁场中不一定受安培力．安培力是大量运动电荷所受洛伦兹力的宏观表现．‎ ‎2.‎ 图3－6‎ 磁场中某区域的磁感线，如图3－6所示，则(　　)‎ A．a、b两处的磁感应强度的大小不等，Ba＞Bb B．a、b两处的磁感应强度的大小不等，Ba＜Bb C．同一通电导线放在a处受力一定比放在b处受力大 D．同一通电导线放在a处受力一定比放在b处受力小 解析：选A.由磁感线的疏密可知Ba＞Bb，由通电导线所受安培力与通电导线的放置有关，通电导线放在a处与放在b处受力大小无法确定．‎ ‎3．‎ 图3－7‎ 两个绝缘导体环AA′、BB′大小相同，环面垂直，环中通有相同大小的恒定电流，如图3－7所示，则圆心O处磁感应强度的方向为(AA′面水平，BB′面垂直纸面)(　　)‎ A．指向左上方 B．指向右下方 C．竖直向上 D．水平向右 答案：A ‎4.‎ 图3－8‎ 8‎ 如图3－8所示，垂直纸面放置的两根直导线a和b，它们的位置固定并通有相等的电流I；在a、b沿纸面的连线的中垂线上放有另一直导线c，c可以自由运动．当c中通以电流I1时，c并未发生运动，则可以判定a、b中的电流(　　)‎ A．方向相同都向里 B．方向相同都向外 C．方向相反 D．只要a、b中有电流，c就不可能静止 解析：选C.如果导线c并未发生运动，则导线a、b在导线c处的合磁场方向应平行于导线c，由平行四边形定则和直导线周围磁场分布规律可知，两电流I1、I2方向应相反，故C正确．‎ ‎5.‎ 图3－9‎ 美国发射的航天飞机“发现者”号搭载了一台α磁谱仪，其中一个关键部件是由中国科学院电工研究所设计制造的直径为1200 mm、高为80 mm、中心磁感应强度为0.314 T的永久磁体．它的主要使命是要探测宇宙空间中可能存在的物质，特别是宇宙中反氦原子核．若如图3－9所示的磁谱仪中的4条径迹分别为质子、反质子、α粒子、反氦核的径迹，其中反氦核的径迹为(　　)‎ A．1　　　　　　　　　 B．2‎ C．3 D．4‎ 解析：选B.由速度选择器的特点可知，进入磁场B2的四种粒子的速度v相同．由左手定则可以判断，向左偏转的为反质子和反氦核(带负电)．又根据R＝知RH＜RHe，故2为反氦核的径迹，故B正确．‎ ‎6.‎ 图3－10‎ 如图3－10所示，平行板电容器的两板与电源相连，板间同时有电场和垂直纸面向里的匀强磁场B，一个带电荷量为＋q的粒子以v0为初速度从两板中间沿垂直电磁场方向进入，穿出时粒子的动能减小了，若想使这个带电粒子以v0沿原方向匀速直线运动穿过电磁场，可采用的办法是(　　)‎ A．减小平行板的正对面积 B．增大电源电压 C．减小磁感应强度B D．增大磁感应强度B 8‎ 解析：选BC.带电粒子在正交的电磁场中运动，由于射出时动能小于mv2，可以判定洛伦兹力大于电场力，因此若使带电粒子以v0沿原方向运动，则必须增大电场强度或减小磁感应强度，故C正确，D错误．电场强度可利用公式E＝求出，可知U越大，E越大，故B正确．对于A答案，不改变电压及板间距离，只改变正对面积，不影响电场强度，故A错误．‎ ‎7.‎ 图3－11‎ 由于科学研究的需要，常常将质子(11H)和α粒子(42He)等带电粒子贮存在圆环状空腔中，圆环状空腔置于一个与圆环平面垂直的匀强磁场中，磁感应强度为B.如果质子和α粒子在空腔中做圆周运动的轨迹相同(如图3－11中虚线所示)，磁场也相同，比较质子和α粒子在圆环状空腔中运动的动能EkH和Ekα及周期TH和Tα的大小，有(　　)‎ A．EkH≠Ekα，TH≠Tα B．EkH＝Ekα，TH＝Tα C．EkH≠Ekα，TH＝Tα D．EkH＝Ekα，TH≠Tα 解析：选D.由R＝，Ek＝mv2，可得：R＝，因RH＝Rα，mα＝4mH，qα＝2qH，可得：EkH＝Ekα，由T＝可得TH＝Tα.故D正确．‎ ‎8.‎ 图3－12‎ 如图3－12所示，在x轴上方存在着垂直于纸面向里、磁感应强度为B的匀强磁场．一个不计重力的带电粒子从坐标原点O处以速度v进入磁场，粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成120°角．若粒子穿过y轴正半轴后在磁场中到x轴的最大距离为a，则该粒子的比荷和所带电荷的正负是(　　)‎ A.，正电荷 B.，正电荷 C.，负电荷 D.，负电荷 8‎ 解析：选C.粒子能穿过y轴的正半轴，所以该粒子带负电荷，其运动轨迹如图所示，A点到x轴的距离最大，为R＋R＝a，R＝，得＝，故C正确．‎ ‎9.‎ 图3－13‎ 半径为r的圆形空间内，存在着垂直于纸面向里的匀强磁场，一个带电粒子(不计重力)从A点以速度v0垂直磁场方向射入磁场中，并从B点射出．∠AOB＝120°，如图3－13所示，则该带电粒子在磁场中运动的时间为(　　)‎ A．2πr/3v0‎ B．2πr/3v0‎ C．πr/3v0‎ D.πr/3v0‎ 解析：选D.从弧所对圆心角θ＝60°，知t＝ T＝πm/3qB.但题中已知条件不够，没有此选项，另想办法找规律表示t.由匀速圆周运动t＝/v0，从图示分析有R＝r，则：＝R·θ＝r×＝πr，则t＝/v0＝πr/3v0.所以选项D正确．‎ ‎10.‎ 图3－14‎ 如图3－14所示，光滑绝缘轨道ABP竖直放置，其轨道末端切线水平，在其右侧有一正交的匀强电场、磁场区域，电场竖直向上，磁场垂直纸面向里．一带电小球从轨道上的A点由静止滑下，经P点进入场区后，恰好沿水平方向做直线运动．则可判定(　　)‎ A．小球带负电 B．小球带正电 C．若小球从B点由静止滑下，进入场区后将立即向上偏 D．若小球从B点由静止滑下，进入场区后将立即向下偏 答案：BD ‎11．在匀 8‎ 图3－15‎ 强磁场中置一均匀金属薄片，有一个带电粒子在该磁场中按如图3－15所示轨迹运动．由于粒子穿过金属片时有动能损失，在MN上、下方的轨道半径之比为10∶9，不计粒子的重力及空气的阻力，下列判断中正确的是(　　)‎ A．粒子带正电 B．粒子沿abcde方向运动 C．粒子通过上方圆弧比通过下方圆弧时间长 D．粒子恰能穿过金属片10次 解析：选A.依据半径公式可得r＝，则知道r与带电粒子的运动速度成正比．显然半径大的圆周是穿过金属片前的带电粒子的运动轨迹，半径小的圆周是穿过金属片后的带电粒子的运动轨迹，所以粒子沿edcba方向运动．再依据左手定则可知，带电粒子带正电，A对，B错．依据周期公式可知，带电粒子在磁场中的运动周期与运动速度无关，故选项C也是错误的．半径之比为10∶9，即速度之比为10∶9.依据动能定理解得，粒子能穿过金属片的次数为：n＝100/19.故D是错误的，本题的正确选项为A.‎ ‎12．如图3－16所 图3－16‎ 示，表面粗糙的斜面固定于地面上，并处于方向垂直纸面向外、强度为B的匀强磁场中．质量为m、带电量为＋Q的小滑块从斜面顶端由静止下滑．在滑块下滑的过程中，下列判断正确的是(　　)‎ A．滑块受到的摩擦力不变 B．滑块到达地面时的动能与B的大小无关 C．滑块受到的洛伦兹力方向垂直斜面向下 D．B很大时，滑块可能静止于斜面上 解析：选C.由左手定则知C正确．而Ff＝μFN＝μ(mgcosθ＋Bqv)要随速度增加而变大，A错误．若滑块滑到底端已达到匀速运动状态，应有Ff＝mgsin θ，可得v＝(－cos θ)，可看到v随B的增大而减小．若在滑块滑到底端时还处于加速运动状态，则在B越强时，Ff越大，滑块克服阻力做功越多，到达斜面底端的速度越小，B错误．当滑块能静止于斜面上时应有 mgsin θ＝μmgcos θ，即μ＝tan θ，与B的大小无关，D错误．‎ 二、计算题(本题包括4小题，共40分．解答应写出必要的文字说明、方程式和重要的演算步骤，只写出最后答案的不能得分，有数值计算的题，答案中必须明确写出数值和单位)‎ ‎13．(8分)如图3－17所示 图3－17‎ 8‎ ‎，光滑的平行导轨倾角为θ，处在磁感应强度为B的匀强磁场中，导轨中接入电动势为E、内阻为r的直流电源．电路中有一阻值为R的电阻，其余电阻不计，将质量为m、长度为L的导体棒由静止释放， 求导体棒在释放瞬间的加速度的大小．‎ 解析：受力分析如图所示，导体棒受重力mg、支持力FN和安培力F，由牛顿第二定律：‎ mgsin θ－Fcos θ＝ma①‎ F＝BIL②‎ I＝③‎ 由①②③式可得 a＝gsin θ－.‎ 答案：gsin θ－ ‎14．(10分)如图3－18所示，直线MN上方存在垂直纸面向里、磁感应强度大小为B的匀强磁场，现有一质量为m、带电荷量为＋q的粒子在纸面内以某一速度从A点射入，其方向与MN成30°角，A点到MN的距离为d，带电粒子重力不计．‎ 图3－18‎ ‎(1)当v满足什么条件时，粒子能回到A点；‎ ‎(2)粒子在磁场中运动的时间t.‎ 解析：‎ ‎(1)粒子运动如图所示，由图示的几何关系可知：‎ r＝2＝2d 粒子在磁场中的轨道半径为r，则有Bqv＝m 联立两式，得v＝ 此时粒子可按图中轨道回到A点．‎ ‎(2)由图可知，粒子在磁场中运动的圆心角为300°‎ 8‎ 所以t＝T＝＝.‎ 答案：(1)v＝　(2) ‎15.‎ 图3－19‎ ‎(10分)如图3－19所示，匀强电场区域和匀强磁场区域是紧邻的且宽度相等均为d，电场方向在纸平面内，而磁场方向垂直纸面向里．一带正电粒子从O点以速度v0沿垂直电场方向进入电场．在电场力的作用下发生偏转，从A点离开电场进入磁场，离开电场时带电粒子在电场方向的偏移量为d，当粒子从C点穿出磁场时速度方向与进入电场O点时的速度方向一致，不计带电粒子的重力，求：‎ ‎(1)粒子从C点穿出磁场时的速度v.‎ ‎(2)电场强度和磁感应强度的比值.‎ 解析：(1)粒子在电场中偏转，垂直于电场方向速度v⊥＝v0，平行于电场方向速度v∥，因为d＝v⊥·t＝v0t，d＝·t，所以v∥＝v⊥＝v0，所以v＝＝v0，tanθ＝＝1.因此θ＝45°，即粒子进入磁场时的速度方向与水平方向成45°角斜向右下方．粒子在匀强磁场中做匀速圆周运动，穿出磁场时速度大小为v＝v0，方向水平向右．‎ ‎(2)粒子在电场中运动时，v∥＝at＝·，得E＝.‎ 在磁场中运动轨迹如图所示．‎ 则R＝＝d，‎ 又qvB＝，B＝＝＝，‎ 所以＝v0.‎ 答案：(1)v0，方向水平向右　(2)v0‎ 8‎ ‎16．(12分)如图3－20所示，初速度为零的负离子经电势差为U的电场加速后，从离子枪T中水平射出，经过一段路程后进入水平放置的两平行金属板MN和PQ之间，离子所经空间存在着磁感应强度为B的匀强磁场．不考虑重力作用，离子的比荷q/m在什么范围内，离子才能打在金属板上？‎ 图3－20‎ 解析：在加速过程中，据动能定理有mv2＝qU，由此得离子进入磁场的初速度v＝ .分析离子进入磁场后打到金属板两端的轨迹，如图所示，设半径分别为R1和R2，则离子打到金属板上的条件是R1≤R≤R2，由勾股定理知R2＝d2＋(R1－)2‎ 得R1＝d；‎ 由勾股定理知R2＝(2d)2＋(R2－)2‎ 得R2＝d.‎ 再由R＝及v＝ 可得R＝ ，‎ 所以≤≤.‎ 答案：≤≤ 。‎ ‎ ‎ 8‎