- 2021-04-25 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学 3_1_5课时同步练习 新人教A版选修2-1
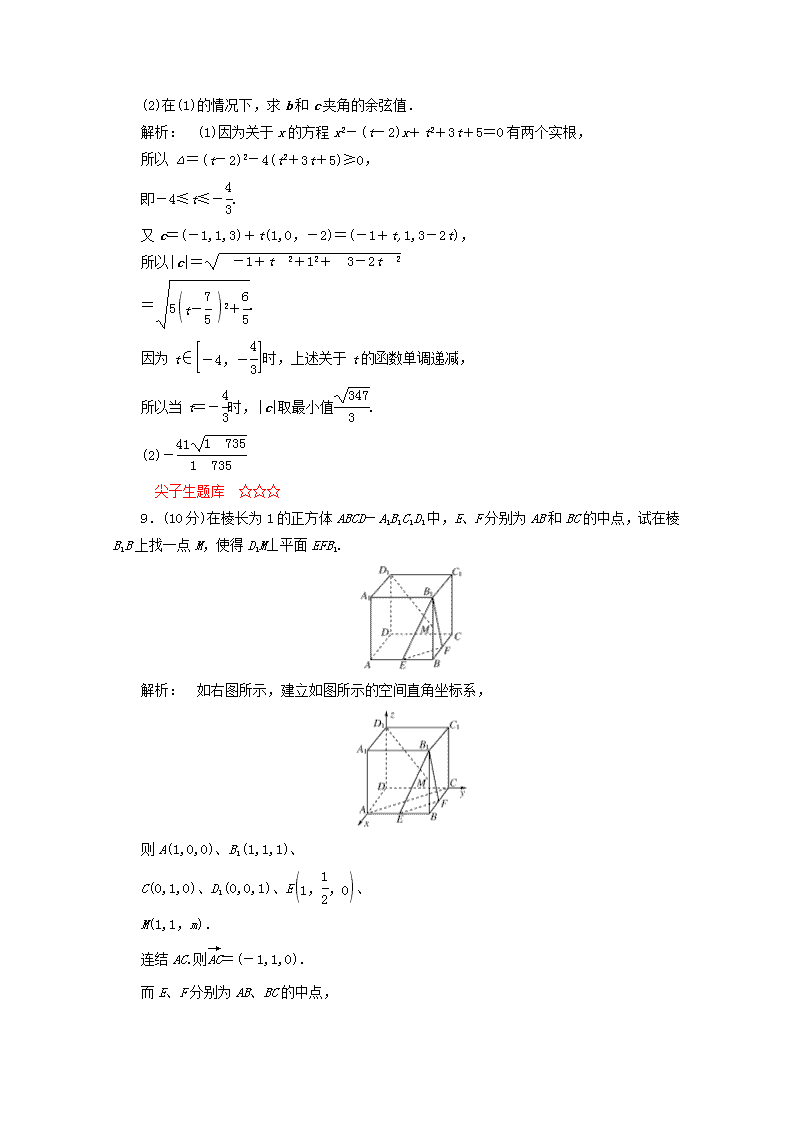
第3章 3.1.5 一、选择题(每小题5分,共20分) 1.已知A(3,4,5),B(0,2,1),O(0,0,0),若=,则C的坐标是( ) A. B. C. D. 解析: =(-3,-2,-4) = ∴C. 答案: A 2.已知a=(2,-3,1),则下列向量中与a平行的是( ) A.(1,1,1) B.(-2,-3,5) C.(2,-3,5) D.(-4,6,-2) 解析: 若b=(-4,6,-2),则b=-2(2,-3,1)=-2a, 所以a∥b. 答案: D 3.若a=(1,λ,2),b=(2,-1,2),且a与b的夹角的余弦为,则λ=( ) A.2 B.-2 C.-2或 D.2或- 解析: 因为a·b=1×2+λ×(-1)+2×2=6-λ, 又因为a·b=|a||b|·cos〈a,b〉=·· =,所以=6-λ, 解得λ=-2或. 答案: C 4.已知a=(1,0,1),b=(-2,-1,1),c=(3,1,0),则|a-b+2c|等于( ) A.3 B.2 C. D.5 解析: ∵a-b+2c=(1,0,1)-(-2,-1,1)+(6,2,0) =(3,1,0)+(6,2,0)=(9,3,0), ∴|a-b+2c|=3. 答案: A 二、填空题(每小题5分,共10分) 5.已知a=(cos α,1,sin α),b=(sin α,1,cos α),则向量a+b与a-b的夹角为________. 解析: a+b=(cos α+sin α,2,sin α+cos α), a-b=(cos α-sin α,0,sin α-cos α), ∴(a+b)·(a-b)=cos2α-sin2α+sin2α-cos2α=0, ∴a+b与a-b的夹角为90°. 答案: 90° 6.已知向量a=(-1,0,1),b=(1,2,3),k∈R,若ka-b与b垂直,则k=________. 解析: 因为(ka-b)⊥b,所以(ka-b)·b=0, 所以ka·b-|b|2=0, 所以k(-1×1+0×2+1×3)-()2=0, 解得k=7. 答案: 7 三、解答题(每小题10分,共20分) 7.已知点A(1,0,0),B(0,1,0),C(0,0,2),求满足DB∥AC,DC∥AB的点D的坐标. 解析: 设点D(x,y,z),则=(-x,1-y,-z),=(-1,0,2),=(-x,-y,2-z),=(-1,1,0), ∵DB∥AC,DC∥AB, ∴∥,∥, 有 解得 所以D(-1,1,2). 8.已知关于x的方程x2-(t-2)x+t2+3t+5=0有两个实根,a=(-1,1,3),b=(1,0,-2),c=a+tb. (1)当|c|取最小值时,求t的值; (2)在(1)的情况下,求b和c夹角的余弦值. 解析: (1)因为关于x的方程x2-(t-2)x+t2+3t+5=0有两个实根, 所以Δ=(t-2)2-4(t2+3t+5)≥0, 即-4≤t≤-. 又c=(-1,1,3)+t(1,0,-2)=(-1+t,1,3-2t), 所以|c|= =. 因为t∈时,上述关于t的函数单调递减, 所以当t=-时,|c|取最小值. (2)- 尖子生题库☆☆☆ 9.(10分)在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为AB和BC的中点,试在棱B1B上找一点M,使得D1M⊥平面EFB1. 解析: 如右图所示,建立如图所示的空间直角坐标系, 则A(1,0,0)、B1(1,1,1)、 C(0,1,0)、D1(0,0,1)、E、 M(1,1,m). 连结AC.则=(-1,1,0). 而E、F分别为AB、BC的中点, 所以==. 又因为=, =(1,1,m-1), 因为D1M⊥平面EFB1, 所以D1M⊥EF,且D1M⊥B1E, 即·=0,且·=0. 所以, 解得m=.查看更多