四川省成都市邛崃市2019-2020学年八年级下学期期末考试数学试题（大邑、简阳）

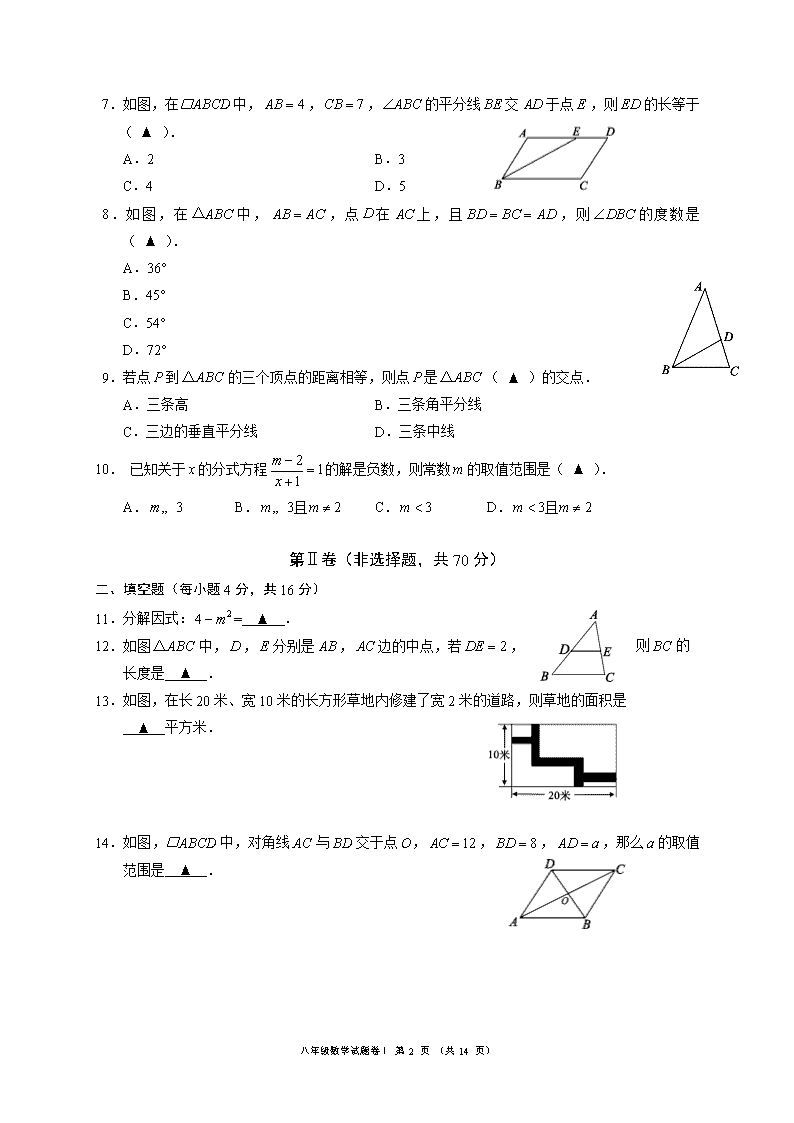
四川省成都市邛崃市2019-2020学年八年级下学期期末考试数学试题（大邑、简阳）

‎2019～2020学年度下期八年级期末质量检测 数 学（卷Ⅰ）‎ A卷（共100分）‎ 第Ⅰ卷（选择题，共30分）‎ 一、选择题（每小题3分，共30分。下列各小题给出的四个选项中，只有一个符合题目要求）‎ ‎ 1．下列标志既是轴对称图形又是中心对称图形的是（ ▲ ）．‎ A． B． C． D．‎ ‎ 2．已知，则下列不等式成立的是（ ▲ ）．‎ A． B． ‎ C． D．‎ ‎ 3．分式值为0时，x的取值是（ ▲ ）．‎ A． B．‎0 ‎ C．1或 D．1‎ ‎ 4．若正多边形的内角和是1080°，则该正多边形的一个外角为（ ▲ ）．‎ A．45° B．60° C．72° D．90°‎ ‎ 5．下列等式中，从左到右的变形是因式分解的是（ ▲ ）．‎ A． B．‎ C． D． ‎ ‎ 6．关于的不等式的解集如图所示，则的取值是（ ▲ ）．‎ A． B． ‎ C． D．‎ 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎ ‎ 7．如图，在□ABCD中，，，的平分线交于点，则的长等于（ ▲ ）．‎ A．2 B．3 ‎ C．4 D．5‎ ‎ 8．如图，在中，，点在上，且，则的度数是（ ▲ ）．‎ A．36° ‎ B．45° ‎ C．54° ‎ D．72°‎ ‎ 9．若点到的三个顶点的距离相等，则点是（ ▲ ）的交点．‎ A．三条高 B．三条角平分线 ‎ C．三边的垂直平分线 D．三条中线 ‎10． 已知关于的分式方程的解是负数，则常数的取值范围是（ ▲ ）．‎ A． B． C． D． ‎ 第Ⅱ卷（非选择题，共70分）‎ 二、填空题（每小题4分，共16分）‎ ‎11．分解因式：= ▲ ．‎ ‎12．如图中，，分别是，边的中点，若，则的长度是 ▲ ．‎ ‎13．如图，在长‎20米、宽‎10米的长方形草地内修建了宽‎2米的道路，则草地的面积是 ‎ ▲ 平方米． ‎ ‎14．如图，□ABCD中，对角线AC与BD交于点O，，，，那么的取值范围是 ▲ ． ‎ 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎ 三、解答题（本大题共小题，共54分，答题应写出文字说明、证明过程或演算步骤）‎ ‎15．（本题满分12分，每小题6分） ‎ ‎（1）分解因式：．‎ ‎▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲‎ ‎（2）解不等式组．‎ ‎▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲‎ ‎16．（本题满分6分）‎ 化简：．‎ ‎▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲‎ ‎17．（本题满分8分）‎ 在平面直角坐标系中的位置如图所示．‎ ‎（1）将向左平移4个单位长度后得到，点、、分别是、、的对应点，请画出，并写出的坐标；‎ ‎（2）将绕点O顺时针旋转90°，得到，点、、分别是、、的对应点，请画出，并写出的坐标．‎ ‎▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲‎ ‎ ‎ ‎18．（本题满分8分）‎ 列方程解应用题 今年1月下旬以来，新冠肺炎疫情在全国范围内迅速蔓延，而比疫情蔓延速度更快的是口罩恐慌．企业复工复产急需口罩，某大型国有企业向生产口罩的A、B两厂订购口罩，向A厂支付了1.32万元，向B厂支付了2.4万元，且在B厂订购的口罩数量是A厂的2倍，B厂的口罩每只比A 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎ 厂低0.2元．求A、B两厂生产的口罩单价分别是多少元？‎ ‎▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲‎ ‎19．（本题满分10分）‎ 在学习一元一次不等式与一次函数中，小明在同一个坐标系中分别作出了一次函数和的图象，分别与轴交于点A、B，两直线交于点C．已知点，，观察图象并回答下列问题：‎ ‎（1）关于的方程的解是 ▲ ；关于的不等式的解集是 ‎ ▲ ；‎ ‎（2）直接写出关于的不等式组的解集；‎ ‎（3）若点，求关于的不等式的解集和的面积．‎ ‎▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲‎ 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎ ‎20．（本题满分10分）‎ 如图1，点D是中边上一动点（不与点B，C重合），连接，取的中点O，过点D作DE∥AC交AB于点E，连接EO，并延长交AC于点，连接．‎ ‎（1）试判断四边形AEDF的形状，并证明你的结论；‎ ‎（2）如图2，当∠BAC = 60°，，AE = 6时，求四边形AEDF的面积；‎ ‎（3）在图1中，在点D的移动过程中，能否构成等腰直角三角形？若能，直接写出∠BAC的度数；若不能，请说明理由．‎ ‎ ‎ ‎ ‎ ‎ （图1） （图2）‎ ‎▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲‎ 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎ B卷（共50分）‎ 一、填空题（每小题4分，共20分）‎ ‎21．已知可以被10和20之间的两个整数分别整除，则这两个数分别是 ▲ ．‎ ‎22．两个全等的直角三角尺，如图所示放置在∠AOB的两边上，其中直角三角尺的短直角边分别与∠AOB的两边重合，两个直角三角尺的长直角边交于点P，连接OP，且OM=ON，若∠AOB = 60°，OM = ‎6 cm，则线段OP= ▲ cm．‎ ‎23．若关于的分式方程无解．则常数的值是 ▲ ．‎ ‎24．如图，Rt的两直角边OA、OB分别在轴和轴上，，，将绕点顺时针旋转得到，直线AC、BD交于点E．点M为直线BD上的动点，点N为轴上的点，若以，，，四点为顶点的四边形是平行四边形，则符合条件的点的坐标为 ▲ ．‎ ‎25．如图，两个全等的等边三角形与，拼成的四边形中，，点，分别为，边上的动点，满足，连接交于点，、分别交于点，．给出下列结论：‎ ‎① 是等边三角形；‎ ‎② ；‎ ‎③ 若，则；‎ ‎④ ；‎ ‎⑤ 面积的最小值为．其中所有正确结论的序号是 ▲ ．‎ 二、解答题（本大题共3小题，共30分。其中26题8分，27题10分，28题12分）‎ ‎26．（本题满分8分）‎ ‎2020年初，“新型冠状病毒”肆虐全国，武汉“封城”。大疫无情人有情，四川在做好疫情防控的同时，向湖北特别是武汉人们伸出了援手，医疗队伍千里驰援、社会各界捐款捐物。某运输公司现有甲、乙两种货车，要将234吨生活物资从成都运往武汉，已知2辆甲车和3辆乙车一次可运送114吨物资；3辆甲车和2辆乙车一次可运送106吨物资。‎ ‎（1）求每辆甲车和每辆乙车一次分别能装运多少吨生活物资？‎ ‎（2）从成都到武汉，已知甲车每辆燃油费2000元，乙车每辆燃油费2600元。在不超载的情况下公司安排甲、乙两种车共10辆将所有生活物资运到武汉，问公司有几种派车方案？哪种方案所用的燃油费最少？最低燃油费是多少？‎ ‎▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲‎ 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎ ‎27．（本题满分10分）‎ 先阅读下面的内容，再解决问题：‎ 问题：对于形如这样的二次三项式，可以用公式法将它分解成的形式．但对于二次三项式，就不能直接运用公式了．此时，我们可以在二次三项式中先加上一项，使它与成为一个完全平方式，再减去，整个式子的值不变，于是有：‎ 像这样，先添一适当项，使式中出现完全平方式，再减去这项，使整个式子的值不变的方法称为“配方法”．利用“配方法”，解决下列问题：‎ ‎（1）分解因式：= ▲ ；‎ ‎（2）若的三边长是，，，且满足，边的长为奇数，求的周长的最小值．‎ ‎（3）当为何值时，多项式有最大值？并求出这个最大值．‎ ‎▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲‎ ‎28．（本题满分12分）‎ 如图1，□ABCD在平面直角坐标系中，已知点、、，点G是对角线AC的中点，过点G的直线分别与边AB、CD边交于点E、F，点P是直线EF上的动点．‎ ‎（1）求点D的坐标和的值；‎ ‎（2）如图2，当直线EF交轴于点，且时，求点的坐标；‎ ‎（3）如图3，当直线EF交轴于点时，在直线EF上是否存在点，使得以、A、C为顶点的三角形是直角三角形？若存在，请直接写出点的坐标；若不存在，请说明理由．‎ ‎▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲‎ 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎ ‎2019～2020学年度下期八年级期末质量检测 数学参考答案及评分标准（卷Ⅰ）‎ A卷（共100分）‎ 一、选择题（每小题3分，共30分。）‎ ‎1～5：DCAAD 6～10：ABACD ‎ 二、填空题（每小题4分，共16分）‎ ‎11． 12． 4 13． 144 14． ‎ 三、解答题（本大题共6小题，共54分）‎ ‎15．（本题满分12分，每小题6分）‎ 解：（1）原式= ------------3分 ‎①‎ ‎ = ------------6分 ‎②‎ ‎（2）‎ 解不等式①得： ------------2分 解不等式②得： ------------4分 ‎∴原不等式组的解集是： ------------6分 ‎16．（本题满分6分）‎ 解：原式= -------------3分 ‎ = -------------5分 ‎ = -------------6分 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎ ‎17．（本题满分分）‎ 解：（1）如下图所示，△A1B‎1C1即为所求；C1（） -------------4分 ‎（2）如下图所示，△A2B‎2C2即为所求；C2（） --------------8分 ‎ ‎ 注：每小问中，画图正确给3分，坐标写正确给1分 ‎ 18．（本题满分8分）‎ 解：设A厂口罩单价x元，则B厂口罩单价（x0.2）元， ----------1分 根据题意得：‎ ‎ --------------4分 解得： ---------------6分 经检验，x=2.2是原方程的解，且符合题意， ---------------7分 ‎∴x0.2=2． ‎ 答：A厂口罩的单价为2.2元，B厂口罩的单价为2元． --------------8分 ‎19．（本题满分10分）‎ 解：（1）（写成“1”不扣分）， ------------4分 ‎（2） -------------6分 ‎（3）当时，由图象可知，‎ 关于的不等式的解集为： -------------8分 ‎ 的面积= -------------10分 ‎20．（本题满分10分）‎ 解：（1）四边形AEDF是平行四边形 -------------1分 ‎∵DE∥AC，∴∠EDO=∠FAO，‎ 又∵点是的中点，∴AO=DO ‎ 在△AFO和△DEO中， ‎ 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎ ‎∴△AFO≌△DEO（ASA） --------------3分 ‎∴AF=DE，又∵DE∥AC ‎∴四边形AEDF是平行四边形 --------------4分 ‎（2）∵∠BAC=60°，∠1=∠2‎ ‎∴ ∠1=∠2=30°‎ 又∵DE∥AC ‎∴ ∠EDA=30°，‎ ‎∴∠EDA=∠1=30° ‎ ‎∴AE=DE 又 由（1）可知四边形AEDF是平行四边形 ‎∴ AO=DO ‎∴ ‎ ‎∴ ∠EOA=90° ‎ 又∵∠1=30° ‎ ‎∴EO=AE=3，‎ 在Rt△AOE中，∵AE=6，∠EAO=30°， ∠AOE=90° ‎ ‎∴EO=3 --------------5分 ‎∴ ---------------6分 由（1）知，四边形AEDF是平行四边形，‎ ‎∴ EF=2EO=6；AD=2AO=‎ 又∵‎ ‎∴ ----------8分（式子1分，计算1分）‎ ‎（3）△AED能是等腰直角三角形，∠BAC的度数为90°或135°------------10分（各1分）‎ 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎ B卷（共50分）‎ 一、填空题（每小题4分，共20分）‎ ‎21．15，17 22． 23．n =1或 24．（2,2）或（6,） 25． ①②③⑤‎ ‎（注：21题只写出一个数字不给分，23题写正确一个给2分，24题写正确一个给2分，25题有错得0分，未写全则选对1个给1分）‎ ‎26．（本题满分8分）‎ 解：（1）设每辆甲车一次可运x吨，每辆乙车一次可运y吨，根据题意得：‎ ‎ --------------2分（正确1个给1分）‎ 解这个方程组得： ‎ 答：每辆甲车和每辆乙车一次分别能装运18吨和26吨生活物资. ----3分（未答不扣分）‎ ‎（2）设运输公司派甲车m辆，则乙车需派辆，由题意得：‎ ‎ -----------4分 解得： -----------5分 又因为m为正整数，所以m=1，2，3，共有3种派车方案 ------------6分 燃油费 ‎∵＜0‎ ‎∴w随m的增大而减小，当m最大时，w最小 ‎∴应派甲车3辆，乙车7辆 ------------7分 即当m=3时，w最小=24200元 -----------8分 ‎（注：若学生用列举法，分别求出m=1，2，3时的燃油费，再选择派车方案也可，算正确3个燃油费给1分，比较大小后确定方案1分）‎ ‎27．（本题满分10分）‎ 解：（1）a2‎8a+15＝（a3）（a5）； ---------------2分 ‎（2）∵a2+b2‎14a8b+65＝0‎ ‎∴（a2‎14a+49）+（b28b+16）＝0 ----------------3分 ‎∴‎ 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎ ‎∴a7＝0，b4＝0，‎ 解得，a＝7，b＝4 --------------------4分 ‎∵△ABC的三边长是a，b，c，∴3＜c＜11， ‎ 又∵c边的长为奇数，∴c＝5，7，9， -------------------5分 当a＝7，b＝4，c＝5时，△ABC的周长最小是：7+4+5＝16 ----------------6分 ‎（3） -----------------7分 ‎ ----------------8分 ‎= -----------------9分 ‎∵，‎ ‎∴当时，多项式有最大值5． ------------------10分 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎ ‎28．（本题满分12分）‎ 解：（1）如图1，过点C作CM⊥y轴于点M，过点D作DN⊥x轴于点N．‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴BC∥AD，BC=AD ‎∴∠BCA=∠CAD 又CM∥x轴，则∠MCA=∠CAN ‎∴∠BCM=∠DAN 又∵∠BMC=∠DNA=90°‎ ‎∴ ≌ ---------------1分 ‎∴ AN=CM=3，DN=BM=2， ‎ ‎∴ ON=2‎ ‎∴ --------------------2分 ‎∵点G是对角线AC的中点，则AG=CG ‎∵四边形ABCD是平行四边形，‎ ‎∴ AB∥CD，‎ ‎∴∠EAC=∠FCA 又∵∠EGA=∠FGC ‎∴ ≌‎ ‎∴ -------------------3分 设直线AC为（）‎ 由题意得：， 解得：‎ ‎∴ ‎ ‎∴ 直线AC交y轴于点X（） ‎ ‎∴‎ ‎∴ -------------------4分 ‎（2）如图2，当直线EF交x轴于点时，设直线EF：（），‎ ‎∵G为AC中点，∴‎ 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎ ‎∴ ，解得 ‎∴‎ 过点B作∥AC，则直线为： -----------5分 联立得： ‎ ‎∴点 ------------------6分 同理，过点D作m∥AC,则直线m为： ---------7分 联立得： ‎ ‎∴点 ‎ ‎∴满足条件的点P有两个，分别是， --------------------8分 ‎（3）存在，满足条件的点P有四个，其坐标分别是：‎ ‎，，， --------------12分（写正确一个给1分）‎ 八年级数学试题卷Ⅰ 第 14 页 （共 14 页）‎