【数学】2020届一轮复习人教版(理)第3章第3讲三角函数的图象与性质学案
第3讲 三角函数的图象与性质
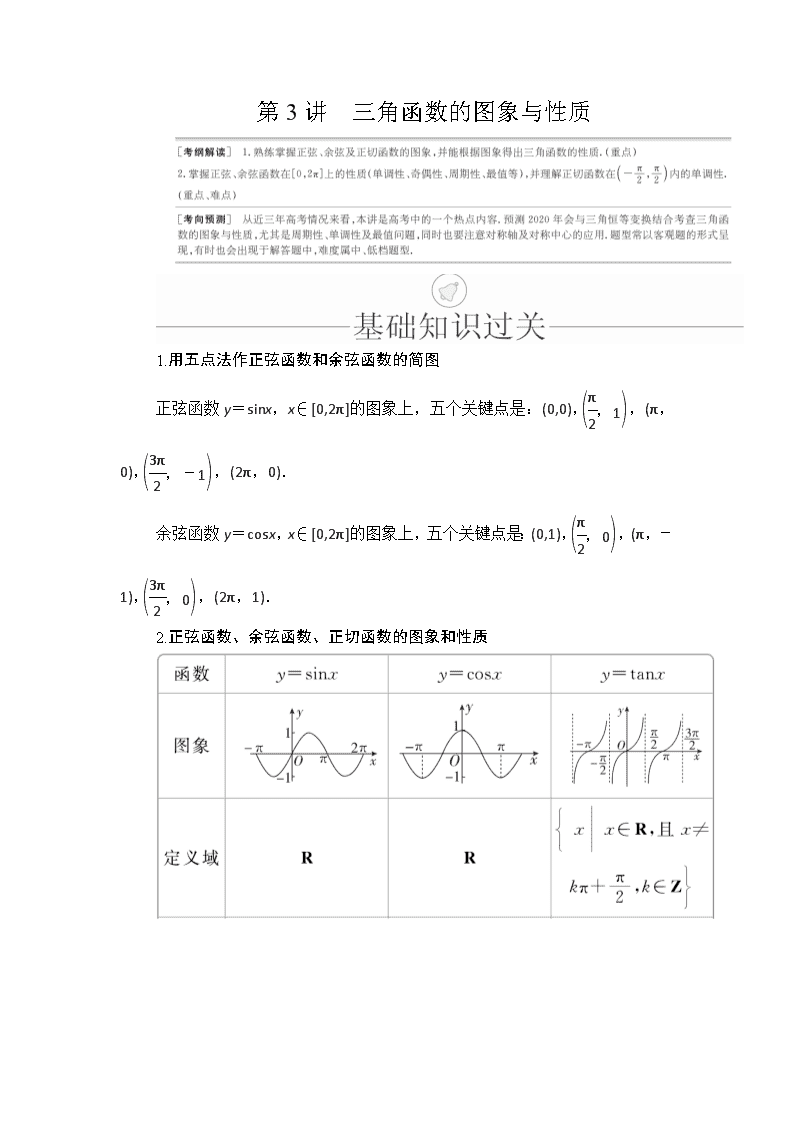
1.用五点法作正弦函数和余弦函数的简图
正弦函数y=sinx,x∈[0,2π]的图象上,五个关键点是:(0,0),,(π,0),,(2π,0).
余弦函数y=cosx,x∈[0,2π]的图象上,五个关键点是:(0,1),,(π,-1),,(2π,1).
2.正弦函数、余弦函数、正切函数的图象和性质
1.概念辨析
(1)y=tanx在整个定义域上是增函数.( )
(2)正弦曲线、余弦曲线相邻两对称中心之间的距离是半个周期.( )
(3)由sin=sin知,是正弦函数y=sinx(x∈R)的一个周期.( )
(4)三角函数中奇函数一般可化为y=Asinωx或y=Atanωx的形式,偶函数一般可化为y=Acosωx+b的形式.( )
答案 (1)× (2)√ (3)× (4)√
2.小题热身
(1)(2017·全国卷Ⅱ)函数f(x)=sin的最小正周期为( )
A.4π B.2π C.π D.
答案 C
解析 函数f(x)=sin的最小正周期T==π.故选C.
(2)函数y=1-2cosx的单调递减区间是________.
答案 [2kπ-π,2kπ](k∈Z)
解析 y=1-2cosx的单调递减区间就是y=cosx的单调递增区间,即[2kπ-π,2kπ](k∈Z).
(3)函数y=3-2sin的最大值为________,此时x=________.
答案 5 +2kπ(k∈Z)
解析 函数y=3-2sin的最大值为3+2=5,此时x+=+2kπ,即x=+2kπ(k∈Z).
(4)cos23°,sin68°,cos97°从小到大的顺序是________.
答案 cos97°
0,函数f(x)=sin在上单调递减,则ω的取值范围是( )
A. B.
C. D.(0,2]
答案 A
解析 由0)的周期为,函数y=Atan(ωx+φ)(ω>0)的周期为求解.
2.函数具有奇偶性的充要条件
函数y=Asin(ωx+φ)(x∈R)是奇函数⇔φ=kπ(k∈Z);
函数y=Asin(ωx+φ)(x∈R)是偶函数⇔φ=kπ+(k∈Z);
函数y=Acos(ωx+φ)(x∈R)是奇函数⇔φ=kπ+(k∈Z);
函数y=Acos(ωx+φ)(x∈R)是偶函数⇔φ=kπ(k∈Z).
3.与三角函数有关的图象的对称性问题
对于函数y=Asin(ωx+φ),其图象的对称轴一定经过函数图象的最高点或最低点,对称中心一定是函数的零点,因此在判断x=x0或点(x0,0)是否是函数的对称轴或对称中心时,可通过检验f(x0)的值进行判断.
1.关于函数y=tan,下列说法正确的是( )
A.是奇函数
B.在区间上单调递减
C.为其图象的一个对称中心
D.最小正周期为π
答案 C
解析 y=tan是非奇非偶函数,A错误;y=tan在区间
上单调递增,B错误;由2x-=得x=+(k∈Z),得函数y=tan的对称中心为,k∈Z,故C正确;函数y=tan的最小正周期为,D错误.
2.(2016·浙江高考)函数y=sinx2的图象是( )
答案 D
解析 由y=sinx2为偶函数,其图象关于y轴对称,可以排除A,C;当x=时,y=sin2=sin≠1,排除B,故选D.
3.(2018·江苏高考)函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(-2,2]上,f(x)=
则f[f(15)]的值为________.
答案
解析 因为f(x+4)=f(x),函数的周期为4,所以f(15)=f(-1),f(-1)==,
所以f[f(15)]=f=cos=.
高频考点 三角函数的图象与性质
考点分析 纵观近年高考中三角函数的试题,其有关性质几乎每年必考,题目较为简单,综合的知识多数为三角函数本章内的知识,通过有效地复习完全可以掌握此类题型的解法,并在高考中拿全分.
[典例1] (2017·全国卷Ⅲ)设函数f(x)=cos,则下列结论错误的是
( )
A.f(x)的一个周期为-2π
B.y=f(x)的图象关于直线x=对称
C.f(x+π)的一个零点为x=
D.f(x)在上单调递减
答案 D
解析 因为f(x)=cos的周期为2kπ(k∈Z),所以f(x)的一个周期为-2π,A项正确.因为f(x)=cos的图象的对称轴为直线x=kπ-(k∈Z),所以y=f(x)的图象关于直线x=对称,B项正确.f(x+π)=cos.令x+=kπ+(k∈Z),得x=kπ-π,当k=1时,x=,所以f(x+π)的一个零点为x=,C项正确.因为f(x)=cos的递减区间为(k∈Z),递增区间为(k∈Z),所以是减区间,是增区间,D项错误.故选D.
[典例2] (2018·北京高考)设函数f(x)=cos(ω>0).若f(x)≤f对任意的实数x都成立,则ω的最小值为________.
答案
解析 结合余弦函数的图象得ω-=2kπ,k∈Z,解得ω=8k+,k∈Z.又∵ω>0,∴当k=0时,ω取得最小值,最小值为.
方法指导 函数y=Asin(ωx+φ)(A>0,ω>0)的性质
(1)奇偶性:φ=kπ(k∈Z)时,函数y=Asin(ωx+φ)为奇函数;φ=kπ+(k∈Z)时,函数y=Asin(ωx+φ)为偶函数.(原理:诱导公式、y=Asinωx为奇函数、y=Acosωx+b为偶函数)
(2)周期性:y=Asin(ωx+φ)存在周期性,其最小正周期为T=.
(3)单调性:根据y=sint和t=ωx+φ的单调性来研究,由-+2kπ≤ωx+φ≤+2kπ,k∈Z得单调递增区间;由+2kπ≤ωx+φ≤+2kπ,k∈Z得单调递减区间.(原理:复合函数同增异减)
(4)对称性:利用y=sinx的对称中心为(kπ,0)(k∈Z)求解,令ωx+φ=kπ(k∈Z),求得x.利用y=sinx的对称轴为x=kπ+(k∈Z)求解,令ωx+φ=kπ+(k∈Z),求得其对称轴.(原理:对称中心、对称轴处函数值的特点)
注意:明确推导以上结论的原理,可以类似推出y=Acos(ωx+φ)、y=Atan(ωx+φ)的相关性质.