数学（理）卷·2017届贵州省铜仁市一中高三上学期第四次月考（2017

数学（理）卷·2017届贵州省铜仁市一中高三上学期第四次月考（2017

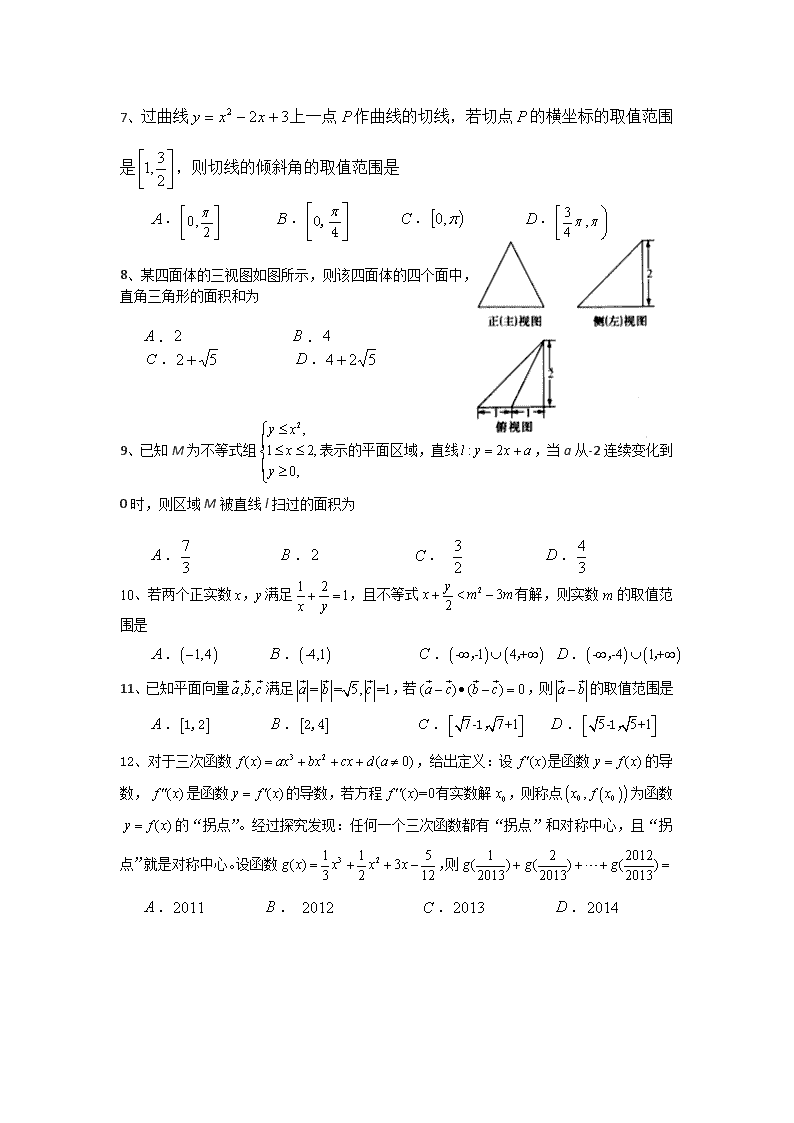
铜仁一中2016年高三第四次月考 理科数学 满分150分，考试时间120分钟 ‎ 参考公式：‎ 球的表面积公式: 其中R表示球的半径 球的体积公式: 其中R表示球的半径 第Ⅰ卷 一、选择题：本大题12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1、设集合，，则集合B的元素个数有 ‎ ．4个 ．3个 ． 2个 ．1个 ‎2、已知复数（为虚数单位），则=‎ ‎． ． ． ．‎ ‎3、已知，则的大小关系为 ‎ ． ． ． ．‎ ‎4、已知等差数列的前项和为，若， 等于 ‎ ‎． ． ． ．‎ ‎5、在中，，是角A，B，C，成等差数列的 ‎ ．必要不充分条件 ．充要条件 ‎ ‎ ．充分不必要条件 ．既不充分也必要条件 ‎6、如图所示程序框图输出的结果是，则判断框内应填的条件是 ‎． ． ． ．‎ ‎7、过曲线上一点作曲线的切线，若切点的横坐标的取值范围是，则切线的倾斜角的取值范围是 ‎ ． ． ． ．‎ 8、 某四面体的三视图如图所示，则该四面体的四个面中，‎ 直角三角形的面积和为 ‎ ． ． ‎ ‎ ． ．‎ ‎9、已知M为不等式组表示的平面区域，直线，当a从-2连续变化到0时，则区域M被直线l扫过的面积为 ‎ ． ． ． ．‎ ‎10、若两个正实数x，y满足，且不等式有解，则实数m的取值范围是 ‎． ． ． ．‎ ‎11、已知平面向量满足，若，则的取值范围是 ‎ ． ． ． ．‎ ‎12、对于三次函数，给出定义：设是函数的导数，是函数的导数，若方程有实数解，则称点为函数的“拐点”。经过探究发现：任何一个三次函数都有“拐点”和对称中心，且“拐点”就是对称中心。设函数，则 ‎ ． ． ． ．‎ 第II卷 本卷包括必考题和选考题两部分，第13～第21题为必考题，每个试题考生都必须作答。第22～第24题为选考题，考生根据要求作答。‎ 二、 填空题：（本大题共4小题，每小题5分。共20分）‎ ‎13、已知是第二象限角，为其终边上一点，且，则等于 。‎ ‎14、若两个非零向量满足，则向量的夹角为， 。 ‎ ‎15、已知四面体中，，，则其内切球半径与外接球半径之差为 。‎ ‎16、将一个真命题中的“平面”换成“直线”、“直线”换成“平面”后仍是真命题，则该命题成为“可换命题”.给出下列四个命题①垂直于同一平面的两直线平行；②垂直于同一平面的两平面平行；③平行于同一直线的两直线平行；④平行于同一平面的两直线平行.（平面不重合、直线不重合）其中是“可换命题”的是 。‎ 三、解答题:（共六题。70分。要求写出证明过程或演算步骤）‎ ‎17、（本小题满分12分） 已知向量，函数的图像经过点，若将图像上的所有点保持纵坐标不变，横坐标变为原来的一半，得到函数 ‎(Ⅰ) 求的单调递增区间；‎ ‎ (Ⅱ)已知 且，‎ ‎18、（本小题满分12分）在数列中，构成公比不为1的等比数列。‎ ‎(1)求数列的通项公式；‎ ‎(2)令，设数列前n项和为，求 ‎19、(本题满分12分)如图，四棱锥的底面是正方形,⊥底面，，点分别在棱上，且⊥平面.‎ ‎（1）求证：⊥；‎ ‎（2）求二面角的余弦值；‎ ‎ ‎ ‎ ‎ ‎ ‎ 20、 ‎（本小题满分12分） 如图，⊥平面，四边形是矩形，分别是的中点.‎ ‎ （1）求证：∥平面；‎ ‎ （2）若二面角为45°，，‎ ‎ ，求点到平面的距离。‎ ‎21、（本小题满分12分）设函数.‎ ‎（1）若函数在定义域上是单调函数，求实数的取值范围； ‎ ‎（2）令，，设是曲线上相异三点，其中.求证：.‎ 请考生在22，23三题中任选一题作答，如果多做，则按所做的第一题记分．做答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．‎ ‎22、（本小题满分10分）【选修4—4：坐标系与参数方程】‎ 在极坐标系中，曲线的方程为，点．以极点为原点，极轴为轴的正半轴建立直角坐标系．‎ ‎（1）求直线的参数方程和曲线的直角坐标方程；‎ ‎（2）若直线与曲线交于、两点，求的值．‎ ‎23、（本小题满分10分）【选修4—5：不等式选讲】‎ 已知函数，．‎ ‎（1）解不等式；‎ ‎（2）若对于，，有，，求证：．‎ 理科数学答案 一． 选择题：本题考查基本概念和基本运算．每小题5分，满分60分．‎ 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 案 B D C A A A B C D C A B 二． 填空题：每小题5分，满分20分．‎ ‎13、 14、 15、 16、ƒ ‎ 三． 解答题：满分70分.‎ ‎17、‎ ‎18、‎ ‎19、‎ ‎（1）证明：∵ABCD是正方形，∴CD⊥AD，‎ ‎∵PA⊥底面ABCD，∴PA⊥CD.‎ ‎∴CD⊥平面PAD ……………………………………3分 ‎∵AM平面PAD，∴CD⊥AM.‎ ‎∵PC⊥平面AMN，∴PC⊥AM.‎ ‎∴AM⊥平面PCD.‎ ‎∴AM⊥PD .…………………………………………6分 ‎（2）解：∵AM⊥平面PCD（已证）.‎ ‎∴AM⊥PM，AM⊥NM.‎ ‎∴∠PMN为二面角P-AM-N的平面角 .…………………………8分 ‎∵PN⊥平面AMN，∴PN⊥NM.‎ 在直角△PCD中，CD=2，PD=2，∴PC=2.‎ ‎∵PA=AD，AM⊥PD，∴M为PD的中点，‎ PM=PD=‎ 由Rt△PMN∽Rt△PCD，得 ∴.‎ ‎ …………………………12分 ‎20、‎ ‎（1）取PC中点M，连结ME、MF. ‎ ‎，即四边形AFME是平行四边形，…………………………2分 ‎ ∴AF//EM，∵AF平在PCE，∴AF∥平面PCE.…………………………………………4分 ‎（2）∵PA⊥平面AC，CD⊥AD，根据三垂线定理知，CD⊥PD ∴∠PDA是二面角 P—CD—B的平面角，则∠PDA=45°……6分 于是，△PAD是等腰直角三角形，‎ AF⊥PD，又AF⊥CD∴AF⊥面PCD.而EM//AF, ∴EM⊥面PCD.又EM平面PEC, ‎ ‎∴面PEC⊥面PCD.……8分 在面PCD内过F作FH⊥PC于H，则FH为点F到平面PCE的距离.…………………10分 由已知，PD=2，PF=‎ ‎∵△PFH∽△PCD ∴……………………12分 注：向量法求此题时，以PA为Z轴，AB为X轴，AD为Y轴，‎ 平面PEC的法向量为(4,-3,3)‎ ‎21、‎ ‎（1）；（2）时，有唯一极小值点，时，有一个极大值点和一个极小值点，时，无极值点；（2）证明见解析.‎ 试题解析：（1）， ‎ ‎∵函数在定义域上是单调函数，∴或在上恒成立. ‎ 若恒成立，得.‎ 若恒成立，即恒成立.‎ ‎∵在上没有最小值，∴不存在实数使恒成立.‎ 综上所述，实数的取值范围是.‎ ‎（2）先证：，即证， ‎ 即证，‎ 令（）， ，, ‎ 所以在 上单调递增，即 ,即有, 所以获证.‎ 同理可证：， ‎ 所以. ‎ ‎22．（1）（为参数），；（2）. ‎ 试题解析：（1）∵化为直角坐标可得，，‎ ‎∴直线的参数方程为：‎ ‎∵，‎ ‎∴曲线的直角坐标方程：，得：，‎ ‎∴，，‎ ‎∴．‎ ‎23．（1）；（2）证明见解析.‎ 试题解析：（1）解：，即，解得．‎ ‎(2)．‎