高考数学复习阶段滚动检测(四)
阶段滚动检测(四)
(第一~七章)
(120分钟 150分)
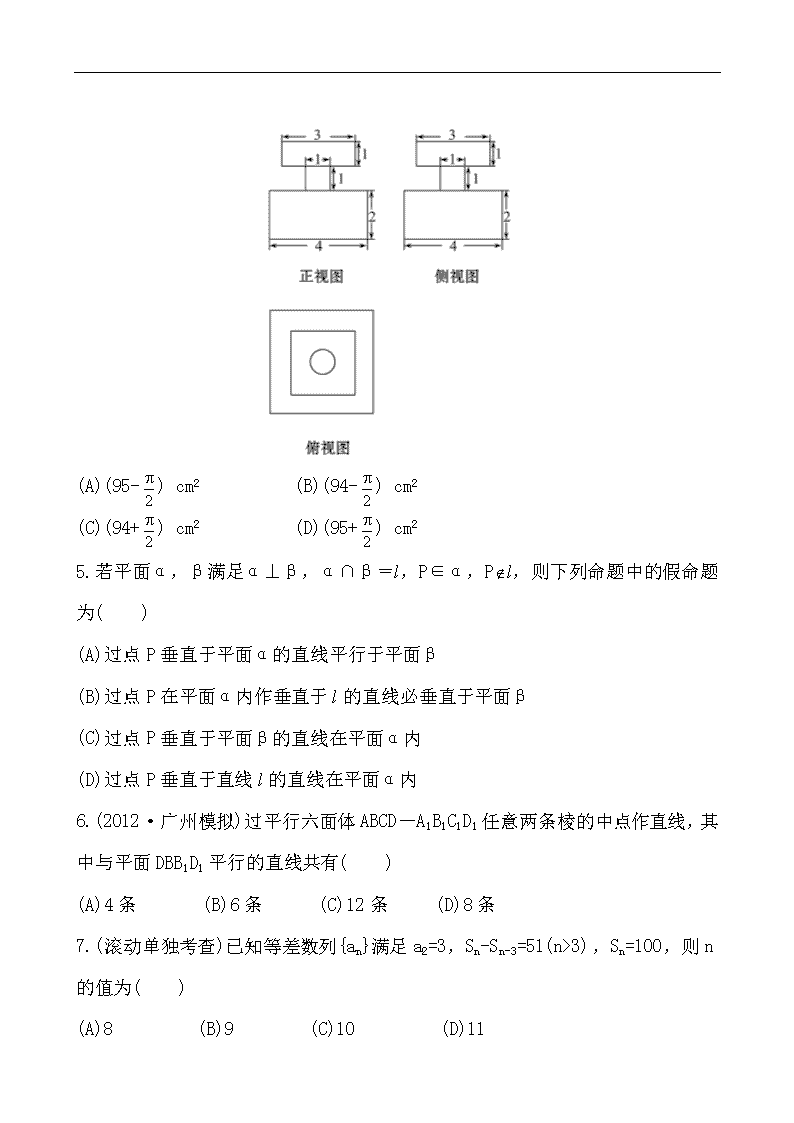
第I卷(选择题 共50分)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. (滚动单独考查)设复数z=1-i,则等于( )
(A)-1+i (B)1+i (C)-1+2i (D)1+2i
2.已知E、F、G、H是空间内四个点,条件甲:E、F、G、H四点不共面,条件乙:直线EF和GH不相交,则甲是乙成立的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
3.(滚动交汇考查)设奇函数f(x)的定义域为R,最小正周期T=3,若f(1)≥1,f(2)=,则a的取值范围是( )
(A)a<-1或a≥ (B)a<-1
(C)-1
3),Sn=100,则n的值为( )
(A)8 (B)9 (C)10 (D)11
8.设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为( )
(A)πa2 (B)πa2 (C)πa2 (D)5πa2
9.(滚动单独考查)已知函数f(x)=cosxsinx(x∈R),给出下列五个命题:
①若f(x1)=-f(x2),则x1=-x2;
②f(x)的最小正周期是2π;
③f(x)在区间[]上是增函数;
④f(x)的图象关于直线x=对称;
⑤当x∈[]时,f(x)的值域为[].
其中正确的命题为( )
(A)①②④ (B)③④⑤ (C)②③ (D)③④
10. (2012·西宁模拟)已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的体积最大(柱体体积=底面积×高)时,其高的值为( )
第Ⅱ卷(非选择题 共100分)
二、填空题(本大题共5小题,每小题4分,共20分.请把正确答案填在题中横线上)
11.母线长为1的圆锥的侧面展开图的圆心角等于,则该圆锥的体积为________.
12.(滚动单独考查)在△ABC中,M是BC的中点,AM=1,点P在AM上且满足则=_______.
13.(滚动单独考查)已知点M(x,y)满足若z=ax+y(a>0)的最小值为3,则a的值为__________.
14.已知m,n是不重合的直线,α,β是不重合的平面,有下列命题:
①若m⊂α,n∥α,则m∥n;
②若m∥n,m⊥α,则n⊥α;
③若m⊥α,m⊂β,则α⊥β;
④若m⊥α,m⊥β,则α∥β.
其中真命题有__________.(写出所有真命题的序号)
15.(滚动单独考查)对于等差数列{an}有如下命题:“若{an}是等差数列,a1=0,s,t 是互不相等的正整数,则有(s-1)at-(t-1)as=0”.类比此命题,给出等比数列{bn}相应的一个正确命题是____________.
三、解答题(本大题共6小题,共80分.解答时应写出必要的文字说明、证明过程或演算步骤)
16.(13分)(2012·太原模拟)如图甲,在平面四边形ABCD中,已知∠A=45°,
∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
(1)求证:DC⊥平面ABC;
(2)设CD=a,求三棱锥A-BFE的体积.
17.(13分)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)在DE上是否存在一点P,使直线BP和平面BCE所成的角为30°?
18.(13分) (滚动单独考查)设Sn为数列{an}的前n项和,Sn=λan-1(λ为常数,n=1,2,3,…).
(1)若a3=a22,求λ的值;
(2)是否存在实数λ,使得数列{an}是等差数列?若存在,求出λ的值;若不存在,请说明理由.
(3)当λ=2时,若数列{bn}满足bn+1=an+bn(n=1,2,3,…),且b1=,令cn=求数列{cn}的前n项和Tn.
19.(13分)(2011·安徽高考)如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.
(1)证明直线BC∥EF;
(2)求棱锥F-OBED的体积.
20.(14分)一个多面体的三视图及直观图如图所示:
(1)求异面直线AB1与DD1所成角的余弦值;
(2)试在平面ADD1A1中确定一个点F,使得FB1⊥平面BCC1B1;
(3)在(2)的条件下,求二面角F―CC1―B的余弦值.
21.(14分) (2012·长春模拟)如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.
(1)求证:BD1∥平面A1DE;
(2)求证:D1E⊥A1D;
(3)在线段AB上是否存在点M,使二面角D1-MC-D的大小为?若存在,求出AM的长;若不存在,请说明理由.
答案解析
1.【解析】选D.
2.【解析】选A.点E、F、G、H四点不共面可以推出直线EF和GH不相交;但由直线EF和GH不相交不一定能推出E、F、G、H四点不共面,例如:EF和GH平行,这也是直线EF和GH不相交的一种情况,但E、F、G、H四点共面.故甲是乙成立的充分不必要条件.
3.【解析】选C.由条件知f(2)=f(3-1)=f(-1)=-f(1),故,解得-10时,由线性规划知,
当直线y=-ax+z过点B(1,0)时,z有最小值,则
zmin=a=3.
答案:3
14.【解析】①若m⊂α,n∥α,则m,n不一定平行,假命题;
②若m∥n,m⊥α,则n⊥α,真命题;③若m⊥α,m⊂β,则α⊥β,真命题;④若m⊥α,m⊥β,则α∥β,真命题.
答案:②③④
15.【解析】从等差数列到等比数列的类比,等差数列中+、-、×、÷类比到等比数列经常是×,÷,( )n,,0类比1.
故若{bn}是等比数列,b1=1,s、t是互不相等的正整数,则=1.
答案: 若{bn}是等比数列,b1=1,s、t是互不相等的正整数,则有
16.【解析】(1)在图甲中,∵AB=BD且∠A=45°,∴∠ADB=45°,∠ABD=90°,即AB⊥BD,在图乙中,∵平面ABD⊥平面BDC,且平面ABD∩平面BDC=BD,∴AB⊥底面BDC,∴AB⊥CD.又∠DCB=90°,∴DC⊥BC,且AB∩BC=B,
∴DC⊥平面ABC.
(2)∵E、F分别为AC、AD的中点,∴EF∥CD,又由(1)知,DC⊥平面ABC,
∴EF⊥平面ABC,∴在图甲中,∵∠ADC=105°,
∴∠BDC=60°,∠DBC=30°.
由CD=a得BD=2a,BC=a,EF=CD=a,∴
∴,∴.
17.【解析】设AD=DE=2AB=2a,建立如图所示的空间直角坐标系Axyz,
则A(0,0,0),B(0,0,a),C(2a,0,0),D(a,,0),E(a,,2a),
∵F为CD的中点,∴F().(1)=(),
∵AF平面BCE,∴AF∥平面BCE.
(2)∵ ∴
∴又CD∩DE=D,∴AF⊥平面CDE,又AF∥平面BCE,
∴平面BCE⊥平面CDE.
(3)存在.设平面BCE的一个法向量为=(x,y,z),由,可得:x++z=0,2x-z=0,取=(1,,2).
设存在P(a, ,ta)满足题意,
则 (0≤t≤2),
设BP和平面BCE所成的角为θ,则
解得:t=3±,又∵t∈[0,2],故取t=3-.
∴存在使直线BP和平面BCE所成的角为30°.
【变式备选】如图,在四棱锥S-ABCD中,底面ABCD是正方形,
其他四个侧面都是等边三角形,AC与BD的交点为O,E为
侧棱SC上一点.
(1)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(2)求证:平面BDE⊥平面SAC;
(3)当二面角E-BD-C的大小为45°时,试判断点E在SC上的位置,并说明理由.
【解析】(1)连接OE,由条件可得SA∥OE.
因为SA平面BDE,OE⊂平面BDE, 所以 SA∥平面BDE.
(2)由题意知SO⊥平面ABCD,AC⊥BD.故建立如图所示的空间直角坐标系.
设四棱锥S-ABCD的底面边长为2,则O(0,0,0),S(0,0,),
A(,0,0),B(0,,0),C(-,0,0),D(0,-,0).
所以=(-2,0,0), =(0,-2,0).
设CE=a(0
查看更多