【精品试卷】中考数学一轮复习 专题测试11 一次函数（培优提高）（教师版）

【精品试卷】中考数学一轮复习 专题测试11 一次函数（培优提高）（教师版）

专题 11 一次函数（专题测试-提高） 学校:___________姓名：___________班级：___________考号：___________ 一、选择题（共 12 小题，每小题 4 分，共 48 分） 1．（2018·江苏中考真题）在平面直角坐标系中，过点（1,2）作直线 l，若直线 l 与两坐标轴围成的三角形面 积为 4，则满足条件的直线 l 的条数是（ ） A．5 B．4 C．3 D．2 【答案】C 【详解】设直线 l 解析式为：y=kx+b，则 l 与 x 轴交于点 A（- b k ，0），与 y 轴交于点 B（0，b）， ∴ 2 1 42AOB k b bS bk          ， ∴（2-k）2=8|k|， ∴k2-12k+4=0 或（k+2）2=0， ∴k=6±4 2 或 k=-2， ∴满足条件的直线有 3 条， 故选 C. 2．（2019·江苏中考模拟）已知直线 y＝﹣x+2 与直线 y＝2x+6 相交于点 A，与 x 轴分别交于 B，C 两点，若 点 D（a， 1 2 a+1）落在△ABC 内部（不含边界），则 a 的取值范围是（ ） A．﹣3＜a＜2 B． 22 3a   C． 4 03 a   D．﹣2＜a＜2 【答案】B 【详解】 已知直线 y＝﹣x+2 与直线 y＝2x+6 相交于点 A，与 x 轴分别交于 B，C 两点， 根据一次函数图象的性质，可以得到如图所示示意图， ∵点 D（a， 1 2 a+1）落在△ABC 内部（不含边界）， ∴列不等式组 1 1 2 62 1 1 22 1 1 02 a a a a a              ， 解得：﹣2＜a＜ 2 3 ， 故选 B． 3．（2018·江苏中考真题）如图，平面直角坐标系 xOy 中，点 A 的坐标为（9，6），AB⊥y 轴，垂足为 B， 点 P 从原点 O 出发向 x 轴正方向运动，同时，点 Q 从点 A 出发向点 B 运动，当点 Q 到达点 B 时，点 P、Q 同时停止运动，若点 P 与点 Q 的速度之比为 1：2，则下列说法正确的是（ ） A．线段 PQ 始终经过点（2，3） B．线段 PQ 始终经过点（3，2） C．线段 PQ 始终经过点（2，2） D．线段 PQ 不可能始终经过某一定点 【答案】B 【解析】 当 OP=t 时，点 P 的坐标为（t，0），点 Q 的坐标为（9﹣2t，6）． 设直线 PQ 的解析式为 y=kx+b（k≠0）， 将 P（t，0）、Q（9﹣2t，6）代入 y=kx+b，得， 0 ( 2 ) 6 kt b t k b       ，解得： 2 3 2 3 k t tb t       ， ∴直线 PQ 的解析式为 y= 2 3 t x+ 2 3 t t  ． ∵x=3 时，y=2， ∴直线 PQ 始终经过（3，2）， 故选：B． 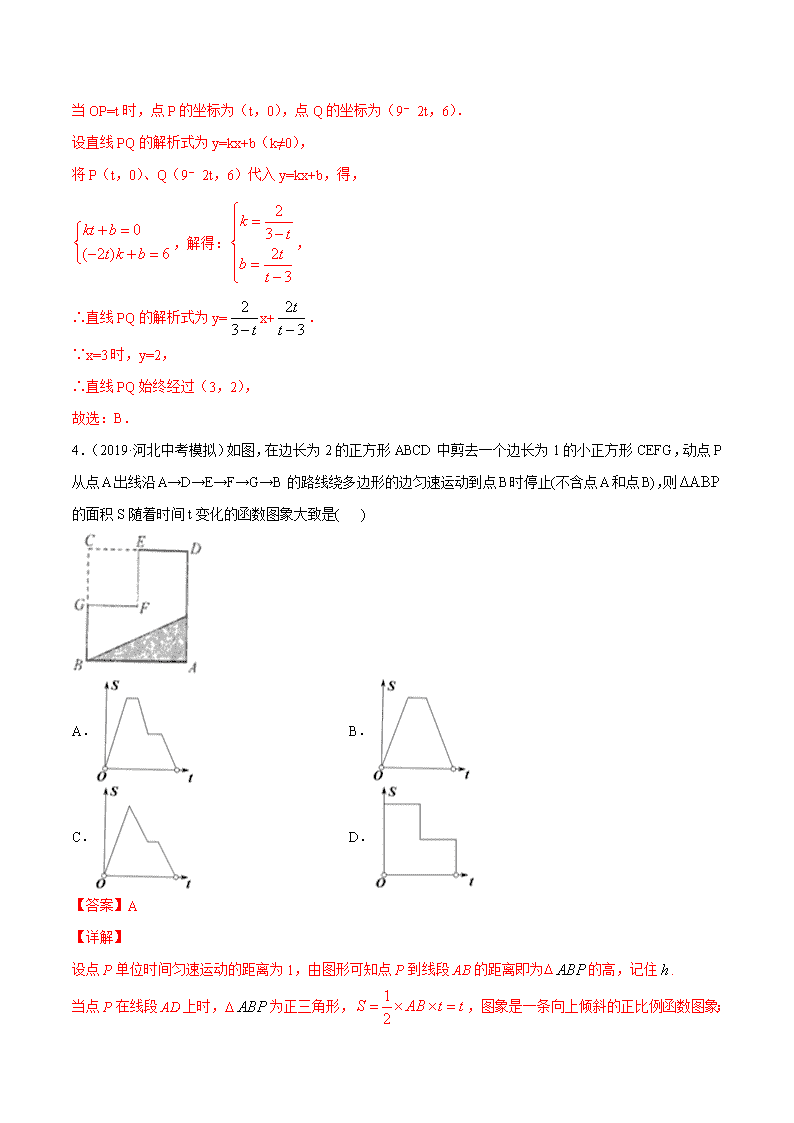4．（2019·河北中考模拟）如图，在边长为 2 的正方形 ABCD 中剪去一个边长为 1 的小正方形 CEFG，动点 P 从点 A 出线沿 A→D→E→F→G→B 的路线绕多边形的边匀速运动到点 B 时停止(不含点 A 和点 B)，则 ΔABP 的面积 S 随着时间 t 变化的函数图象大致是( ) A． B． C． D． 【答案】A 【详解】 设点 P 单位时间匀速运动的距离为 1，由图形可知点 P 到线段 AB 的距离即为 ABP 的高，记住 h . 当点 P 在线段 AD 上时， ABP 为正三角形， 1 2S AB t t    ，图象是一条向上倾斜的正比例函数图象； 当点 P 在线段 DE 上时， 1 22S AB h    ，图象是一条平行于 x 轴的常数函数图象； 当点 P 在线段 EF 上时， 2 ( 3) 5h AD EP t t       ， 1 52S AB h t     ，图象是一条向下倾斜 的一次函数图象； 当点 P 在线段 FG 上时， 1h GB  ， 1 12S AB h    ，图象是一条平行于 x 轴的常数函数图象 当点 P 在线段 GB 上时， 1 ( 5) 6h GB GP t t       ， 1 62S AB h t     ，图象是一条向下倾斜 的一次函数图象. 综上所述只有 B 项的图像符合题意. 5．（2019·中山市坦洲中学中考模拟）小刚从家去学校，先匀速步行到车站，等了几分钟后坐上了公交车， 公交车匀速行驶一段时后到达学校，小刚从家到学校行驶路程 s（单位：m）与时间 r（单位：min）之间函 数关系的大致图象是（ ） A． B． C． D． 【答案】B 【详解】小刚从家到学校，先匀速步行到车站，因此 S 随时间 t 的增长而增长，等了几分钟后坐上了公交车， 因此时间在增加，S 不增长，坐上了公交车，公交车沿着公路匀速行驶一段时间后到达学校，因此 S 又随时 间 t 的增长而增长， 故选 B． 6．（2018·四川中考真题）已知直线 y1=kx+1（k＜0）与直线 y2=mx（m＞0）的交点坐标为（ 1 2 ， 1 2 m），则 不等式组 mx﹣2＜kx+1＜mx 的解集为（ ） A．x> 1 2 B． 1 2 0， ∴函数 y=(k−2)x+1−k 图象经过一、二、四象限， 故选 B. 二、填空题（共 5 小题，每小题 4 分，共 20 分） 13．（2018·重庆中考真题）一天早晨，小玲从家出发匀速步行到学校，小玲出发一段时间后，她的妈妈发现 小玲忘带了一件必需的学习用品，于是立即下楼骑自行车，沿小玲行进的路线，匀速去追小玲，妈妈追上 小玲将学习用品交给小玲后，立即沿原路线匀速返回家里，但由于路上行人渐多，妈妈返回时骑车的速度 只是原来速度的一半，小玲继续以原速度步行前往学校，妈妈与小玲之间的距离 y（米）与小玲从家出发后 步行的时间 x（分）之间的关系如图所示（小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略 不计）．当妈妈刚回到家时，小玲离学校的距离为_____米． 【答案】200 【详解】 由图象得：小玲步行速度：1200÷30=40（米/分）， 由函数图象得出，妈妈在小玲 10 分后出发，15 分时追上小玲， 设妈妈去时的速度为 v 米/分， （15-10）v=15×40， v=120， 则妈妈回家的时间：15 40 60  =10， （30-15-10）×40=200． 故答案为 200． 14．（2019·山东中考模拟）如图，直线 1 42y x  与坐标轴交于 A，B 两点，在射线 AO 上有一点 P，当△ APB 是以 AP 为腰的等腰三角形时，点 P 的坐标是________________. 【答案】   3,0 , 4 5 8,0  【详解】 当 y=0 时，x=-8，即 A（-8，0）， 当 x=0 时，y=4，即 B（0，4）， ∴OA=8，OB=4 在 Rt△ABO 中，AB= 2 2 4 5AO BO  , 若 AP=AB=4 5 ，则 OP=AP-AO=4 5 -8 ∴点 P（4 5 -8，0） 若 AP'=BP'，在 Rt△BP'O 中，BP'2=BO2+P'O2=16+（AO-BP'）2． ∴BP'=AP'=5 ∴OP'=3 ∴P'（-3，0） 综上所述：点 P（-3，0），（4 5 -8，0） 故答案为：（-3，0），（4 5 -8，0） 15．（2018·江苏中考真题）如图，一次函数 y=kx+b 的图象与 x 轴、y 轴分别相交于 A、B 两点，⊙O 经过 A， B 两点，已知 AB=2，则 k b 的值为__________． 【答案】 2 2  【解析】 由图形可知：△OAB 是等腰直角三角形，OA=OB ∵AB=2，OA2+OB2=AB2， ∴OA=OB= 2 2 ， ∴A 点坐标是（ 2 2 ，0），B 点坐标是（0， 2 2 ）， ∵一次函数 y=kx+b 的图象与 x 轴、y 轴分别相交于 A、B 两点， ∴将 A，B 两点坐标带入 y=kx+b，得 k=-1，b= 2 2 ， ∴ k b =- 2 2 . 故答案为：- 2 2 . 16．（2019·庆云县徐园子乡初级中学中考模拟）在平面直角坐标系中，直线 l：y=x﹣1 与 x 轴交于点 A1， 如图所示依次作正方形 A1B1C1O、正方形 A2B2C2C1、…、正方形 AnBnCnCn﹣1，使得点 A1、A2、A3、…在直 线 l 上，点 C1、C2、C3、…在 y 轴正半轴上，则点 Bn 的坐标是_____． 【答案】（2n﹣1，2n﹣1）． 【详解】 解：∵y=x-1 与 x 轴交于点 A1， ∴A1 点坐标（1，0）， ∵四边形 A1B1C1O 是正方形， ∴B1 坐标（1，1）， ∵C1A2∥x 轴， ∴A2 坐标（2，1）， ∵四边形 A2B2C2C1 是正方形， ∴B2 坐标（2，3）， ∵C2A3∥x 轴， ∴A3 坐标（4，3）， ∵四边形 A3B3C3C2 是正方形， ∴B3（4，7）， ∵B1（20，21-1），B2（21，22-1），B3（22，23-1），…， ∴Bn 坐标（2n-1，2n-1）． 故答案为（2n-1，2n-1）． 17．（2018·广西中考模拟）已知一次函数 y=2x+b，它的图象与两坐标轴围成的面积等于 4，则 b=_______． 【答案】4 或﹣4 【解析】 ∵令 x=0,则 y=b;令 y=0,则 x= 2 b , ∴一次函数 y=2x+b 与坐标轴的交点分别为(0,b),( 2 b ,0), ∵一次函数 y=2x+b 与坐标轴围成的三角形面积是 4, ∴ 1 42 2 bb    ,解得 b=±4, 故答案为 4 或-4. 三、解答题（共 4 小题，每小题 8 分，共 32 分） 18．（2019·广东中考模拟）益马高速通车后，将桃江马迹塘的农产品运往益阳的运输成本大大降低．马迹塘 一农户需要将 A，B 两种农产品定期运往益阳某加工厂，每次运输 A，B 产品的件数不变，原来每运一次的 运费是 1200 元，现在每运一次的运费比原来减少了 300 元，A，B 两种产品原来的运费和现在的运费（单 位：元∕件）如下表所示： 品种 A B 原来的运费 45 25 现在的运费 30 20 （1）求每次运输的农产品中 A，B 产品各有多少件？ （2）由于该农户诚实守信，产品质量好，加工厂决定提高该农户的供货量，每次运送的总件数增加 8 件， 但总件数中 B 产品的件数不得超过 A 产品件数的 2 倍，问产品件数增加后，每次运费最少需要多少元？ 【答案】（1）每次运输的农产品中 A 产品有 10 件，每次运输的农产品中 B 产品有 30 件，（2）产品件数增 加后，每次运费最少需要 850 元． 【详解】 （1）设每次运输的农产品中 A 产品有 x 件，每次运输的农产品中 B 产品有 y 件， 根据题意得： 45 25 1200 30 20 1200 300 x y x y     ＝ ＝ ， 解得： 10 30 x y    ＝ ＝ ， 答：每次运输的农产品中 A 产品有 10 件，每次运输的农产品中 B 产品有 30 件， （2）设增加 m 件 A 产品，则增加了（8-m）件 B 产品，设增加供货量后得运费为 W 元， 增加供货量后 A 产品的数量为（10+m）件，B 产品的数量为 30+（8-m）=（38-m）件， 根据题意得：W=30（10+m）+20（38-m）=10m+1060， 由题意得：38-m≤2（10+m）， 解得：m≥6， 即 6≤m≤8， ∵一次函数 W 随 m 的增大而增大 ∴当 m=6 时，W 最小=850， 答：产品件数增加后，每次运费最少需要 850 元． 19．（2018·河北中考真题）如图，直角坐标系 xOy 中，一次函数 y=﹣ 1 2 x+5 的图象 l1 分别与 x，y 轴交于 A， B 两点，正比例函数的图象 l2 与 l1 交于点 C（m，4）． （1）求 m 的值及 l2 的解析式； （2）求 S△AOC﹣S△BOC 的值； （3）一次函数 y=kx+1 的图象为 l3，且 11，l2，l3 不能围成三角形，直接写出 k 的值． 【答案】（1）m=2，l2 的解析式为 y=2x；（2）S△AOC﹣S△BOC=15；（3）k 的值为 3 2 或 2 或﹣ 1 2 ． 【详解】（1）把 C（m，4）代入一次函数 y=﹣ 1 2 x+5，可得 4=﹣ 1 2 m+5， 解得 m=2， ∴C（2，4）， 设 l2 的解析式为 y=ax，则 4=2a， 解得 a=2， ∴l2 的解析式为 y=2x； （2）如图，过 C 作 CD⊥AO 于 D，CE⊥BO 于 E，则 CD=4，CE=2， y=﹣ 1 2 x+5，令 x=0，则 y=5；令 y=0，则 x=10， ∴A（10，0），B（0，5）， ∴AO=10，BO=5， ∴S△AOC﹣S△BOC= 1 2 ×10×4﹣ 1 2 ×5×2=20﹣5=15； （3）一次函数 y=kx+1 的图象为 l3，且 11，l2，l3 不能围成三角形， ∴当 l3 经过点 C（2，4）时，k= 3 2 ； 当 l2，l3 平行时，k=2； 当 11，l3 平行时，k=﹣ 1 2 ； 故 k 的值为 3 2 或 2 或﹣ 1 2 ． 20．（2018·山东中考模拟）赛龙舟是端午节的主要习俗，某市甲乙两支龙舟队在端午节期间进行划龙舟比赛， 从起点 A 驶向终点 B，在整个行程中，龙舟离开起点的距离 y（米）与时间 x（分钟）的对应关系如图所示， 请结合图象解答下列问题： （1）起点 A 与终点 B 之间相距多远？ （2）哪支龙舟队先出发？哪支龙舟队先到达终点？ （3）分别求甲、乙两支龙舟队的 y 与 x 函数关系式； （4）甲龙舟队出发多长时间时两支龙舟队相距 200 米？ 【答案】（1）3000 米；（2）甲龙舟队先出发，乙龙舟队先到达终点；（3）y=200x﹣1000（5≤x≤20）；（4）甲 龙舟队出发 5 3 或 10 或 15 或 70 3 分钟时，两支龙舟队相距 200 米 【解析】 解：（1）由图可得，起点 A 与终点 B 之间相距 3000 米； （2）由图可得，甲龙舟队先出发，乙龙舟队先到达终点； （3）设甲龙舟队的 y 与 x 函数关系式为 y=kx，把（25，3000）代入，可得 3000=25k，解得 k=120，∴甲龙 舟队的 y 与 x 函数关系式为 y=120x（0≤x≤25），设乙龙舟队的 y 与 x 函数关系式为 y=ax+b，把（5，0），（20， 3000）代入，可得： 0 5 3000 20 a b a b      ，解得： 200 1000 a b     ，∴乙龙舟队的 y 与 x 函数关系式为 y=200x﹣ 1000（5≤x≤20）； （4）令 120x=200x﹣1000，可得 x=12.5，即当 x=12.5 时，两龙舟队相遇，当 x＜5 时，令 120x=200，则 x= 5 3 （符合题意）； 当 5≤x＜12.5 时，令 120x﹣（200x﹣1000）=200，则 x=10（符合题意）； 当 12.5＜x≤20 时，令 200x﹣1000﹣120x=200，则 x=15（符合题意）； 当 20＜x≤25 时，令 3000﹣120x=200，则 x= 70 3 （符合题意）； 综上所述，甲龙舟队出发 5 3 或 10 或 15 或 70 3 分钟时，两支龙舟队相距 200 米． 21．（2018·山东中考真题）为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高 科技设备，每台设备成本价为 30 万元,经过市场调研发现,每台售价为 40 万元时,年销售量为 600 台;每台售 价为 45 万元时,年销售量为 550 台.假定该设备的年销售量 y(单位:台)和销售单价 x (单位:万元)成一次函数关 系. (1)求年销售量 y 与销售单价 x 的函数关系式; (2)根据相关规定,此设备的销售单价不得高于 70 万元,如果该公司想获得 10000 万元的年利润.则该设备的销 售单价应是多少万元? 【答案】（1） 10 1000y x   ；（2）该公可若想获得 10000 万元的年利润，此设备的销售单价应是 50 万 元. 【解析】 （1）设年销售量 y 与销售单价 x 的函数关系式为 y=kx+b（k≠0），将（40，600）、（45，550）代入 y=kx+b， 得： 40 600 45 550 k b k b      ， 解得： 10 1000 k b     ， ∴年销售量 y 与销售单价 x 的函数关系式为 y=﹣10x+1000． （2）设此设备的销售单价为 x 万元/台，则每台设备的利润为（x﹣30）万元，销售数量为（﹣ 10x+1000）台，根据题意得： （x﹣30）（﹣10x+1000）=10000， 整理，得：x2﹣130x+4000=0， 解得：x1=50，x2=80． ∵此设备的销售单价不得高于 70 万元，∴x=50． 答：该设备的销售单价应是 50 万元/台