江西省宜春市上高二中2018-2019学年高二下学期第二次月考试题+数学（理）

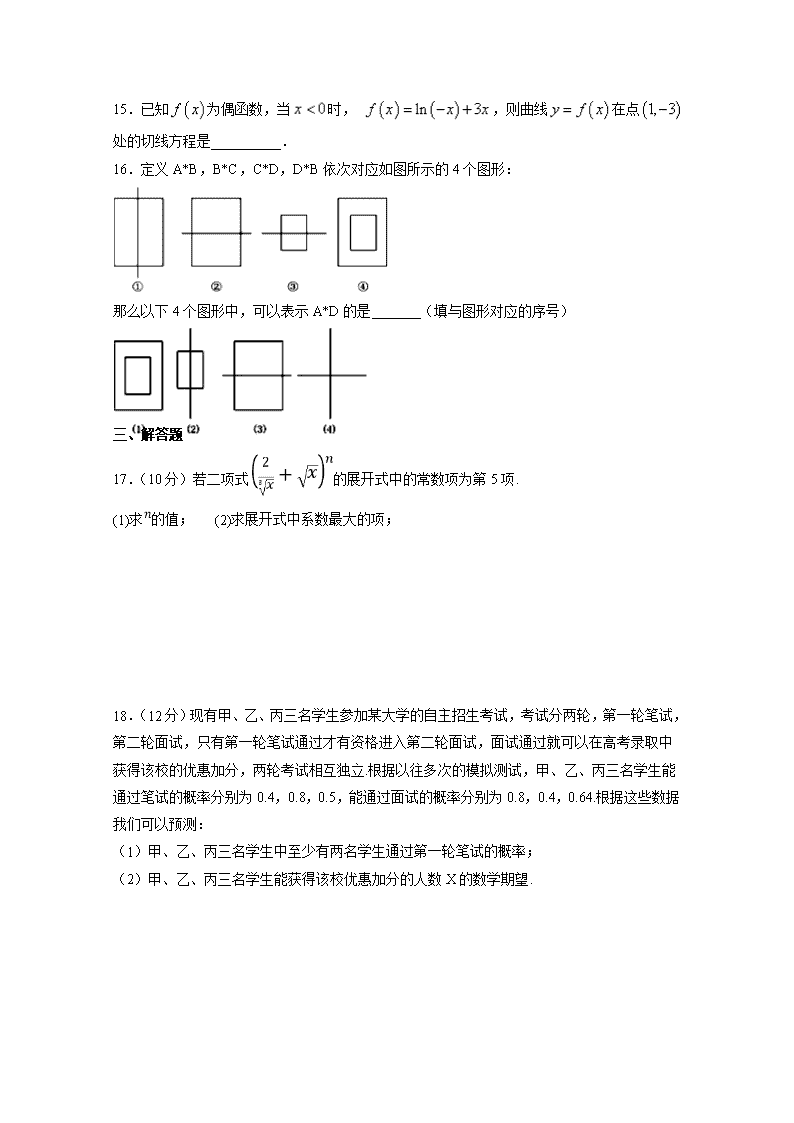
江西省宜春市上高二中2018-2019学年高二下学期第二次月考试题+数学（理）

‎2020届高二年级下学期第二次数学（理科）月考试卷 命题：赵守礼 一、单选题 ‎1．的展开式中各项的二项式系数之和为（ ）‎ A．-1 B．1 C．-512 D．512‎ ‎2．已知两个正态分布密度函数的图象如图所示，则（ ）‎ A． ‎ B．‎ C． ‎ D．‎ ‎3．若函数，为常数，则（ ）‎ A． B． C． D．‎ ‎4．若函数在时取得极值，则（ ）‎ A． B． C． D．‎ ‎5．用数学归纳法证明时，由时的假设到证明时，等式左边应添加的式子是（ ）‎ A． B．‎ C． D．‎ ‎6．设，则（ ）‎ A．2 B． C． D．‎ ‎7．吃零食是中学生中普遍存在的现象，吃零食对学生身体发有有诸多不利影响，影响学生的健康成长，如表是性别与吃零食的列联表：‎ 男 女 总计 喜欢吃零食 ‎30‎ ‎20‎ ‎50‎ 不喜欢吃零食 ‎20‎ ‎30‎ ‎50‎ 总计 ‎50‎ ‎50‎ ‎100‎ 附：K2=，‎ P（K2≥k0）‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ 根据以上数据，你有多大把握认为“喜欢吃零食与性别有关”（　　）‎ A．95%以上 B．97.5%以上 C．99%以上 D．85%以上 ‎8．改革开放以来，中国经济飞速发展，科学技术突飞猛进。高铁、核电、桥梁、激光、通信、人工智能、航空航天、移动支付、量子通讯、特高压输电等许多技术都领先于世界。厉害了，我的国！把“厉害了我的国”这六个字随机地排成一排，其中“厉”、“害”这两个字必须相邻（可以交换顺序），“了”、“的”这两个助词不能相邻，则不同排法的种数为（ ）。‎ A．72 B．108 C．144 D．288‎ ‎9．如图所示，点，B是曲线上一点，向矩形内随机投一点，则该点落在图中阴影内的概率为（ ）‎ A． B． C． D．‎ ‎10．已知，若，使得成立，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎11．已知函数，若存在，使得关于的不等式恒成立，则的取值范围为 A． B． C． D．‎ ‎12．已知函数是定义在R上的增函数, ,,则不等式的解集为（ ）‎ A． B． C． D．‎ 二、填空题 ‎13．已知变量之间具有良好的线性关系，若通过10组数据得到的回归方程为，且，则__________．‎ ‎14．已知，若为互质的正整数)，由以上等式，可推测的值，则________.‎ ‎15．已知为偶函数，当时， ，则曲线在点处的切线方程是__________．‎ ‎16．定义A*B，B*C，C*D，D*B依次对应如图所示的4个图形：‎ ‎ ‎ 那么以下4个图形中，可以表示A*D的是_______（填与图形对应的序号）‎ 三、解答题 ‎17．（10分）若二项式的展开式中的常数项为第5项.‎ ‎(1)求的值； (2)求展开式中系数最大的项；‎ ‎18．（12分）现有甲、乙、丙三名学生参加某大学的自主招生考试，考试分两轮，第一轮笔试，第二轮面试，只有第一轮笔试通过才有资格进入第二轮面试，面试通过就可以在高考录取中获得该校的优惠加分，两轮考试相互独立.根据以往多次的模拟测试，甲、乙、丙三名学生能通过笔试的概率分别为0.4，0.8，0.5，能通过面试的概率分别为0.8，0.4，0.64.根据这些数据我们可以预测：‎ ‎（1）甲、乙、丙三名学生中至少有两名学生通过第一轮笔试的概率；‎ ‎（2）甲、乙、丙三名学生能获得该校优惠加分的人数X的数学期望.‎ ‎19．（12分）如图，四棱锥，底面是边长为2的菱形， ，且平面.‎ ‎（1）证明：平面平面；‎ ‎（2）若平面与平面的夹角为，试求线段的长.‎ ‎20．（12分）已知函数．‎ ‎（1）当时，求的单调增区间；‎ ‎（2）若在上是增函数，求a得取值范围．‎ ‎21．（12分）已知椭圆：的一个焦点为，离心率为．设是椭圆长轴上的一个动点，过点且斜率为的直线交椭圆于，两点.‎ ‎（1）求椭圆的方程；‎ ‎（2）求的最大值.‎ ‎22．（12分）已知函数，且时有极大值.‎ ‎（Ⅰ）求的解析式；‎ ‎（Ⅱ）若为的导函数，不等式（为正整数）对任意正实数x恒成立，求的最大值.（注：）.‎ ‎2020届高二年级下学期第二次月考数学（理科）试卷答题卡 一、选择题（每小题5分，共60分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 二、填空题（本大题共4个小题，每小题5分，共20分）‎ ‎13、 14、 15、 16、 ‎ 三、解答题（共70分）‎ ‎17.（10分）‎ ‎18. （12分）‎ ‎19. （12分）‎ ‎20. （12分）‎ ‎21. （12分）‎ ‎22.（12分）‎ ‎2020届高二年级下学期第二次月考数学（理科）试卷答案 ‎1---5．DAADB 6---10．DACCA 11---12．BB ‎13．-2.1 14．41 15． 16．（2）‎ ‎17．解：‎ ‎ (1)因为二项式的展开式的通项公式为，‎ 所以x的指数为.‎ 又因为的展开式中的常数项为第五项，‎ 所以,且，解得n=10. ‎ ‎ (2)因为，其系数为.‎ 设第k+1()项的系数最大，‎ 则， ‎ 化简得即，‎ 因为,所以，即第四项系数最大，且.‎ ‎18.（1）记事件：甲通过第一轮笔试，事件：乙通过第一轮笔试，‎ 事件：丙通过第一轮笔试，事件：至少有两名学生通过第一轮笔试，‎ 则，，.‎ ‎，‎ ‎，‎ ‎，‎ 所以至少有两名学生通过第一轮笔试的概率为。‎ ‎（2）因为甲、乙、丙三名学生中每个人获得优惠加分的概率均为，‎ 所以，故。‎ ‎19．解：‎ ‎（Ⅰ）证明： 平面 ，‎ 四边形是菱形，‎ 又，所以平面，‎ 又平面，所以平面平面．‎ ‎（Ⅱ）取的中点，由题易证，分别以为轴，‎ 建立空间直角坐标系 (如图)，‎ 设． ‎ 所以 设平面的法向量为,根据，‎ 得，‎ 令，则． ‎ 平面的法向量可取， ‎ 由题， ，解得，‎ 所以线段的长为． ‎ ‎20．解：（1）当时，，‎ 所以，由得，或，‎ 故所求的单调递增区间为.‎ ‎（2）由，‎ ‎∵在上是增函数，所以在上恒成立，即恒成立，‎ ‎∵（当且仅当时取等号），所以，即.‎ ‎21．解：（1）由题意，，，根据求出 ‎，则椭圆的方程为. （2）设点（），则直线的方程为，联立得 ，而 ‎，带入韦达定理，，则，而， 即 ，则当时，，的最大值为. ‎ 试题解析：（1）由已知，，，‎ ‎∴ ， 3分 ‎∴ 椭圆的方程为. 4分 ‎（2）设点（），则直线的方程为， 2分 由 消去，得 4分 ‎ 设，，则， 6分 ‎ ∴‎ ‎ 8分 ‎∵， 即 ‎ ‎∴当时，，的最大值为. ‎ ‎22．解：（Ⅰ）由，因为在时f(x)有极大值，‎ 所以，从而得或， ‎ 时，，此时，当时，，当时，‎ ‎，∴在时f(x)有极小值，不合题意，舍去； ‎ 时，，此时，符合题意。‎ ‎∴所求的 . ‎ ‎（Ⅱ）由（1）知，所以等价于等价于 ‎，即， ‎ 记，则,‎ 由，得x＞k+1，所以在(0,k+1)上单调递减，在(k+1,+∞)上单调递增，‎ 所以，‎ 对任意正实数恒成立，等价于，‎ 即， ‎ 记因为在(0,+∞)上单调递减，又，，∵，∴k=1,2,3,4， 故k的最大值为4.‎