- 2021-04-23 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
黔东南州2021年中考数学模拟试题及答案(3)
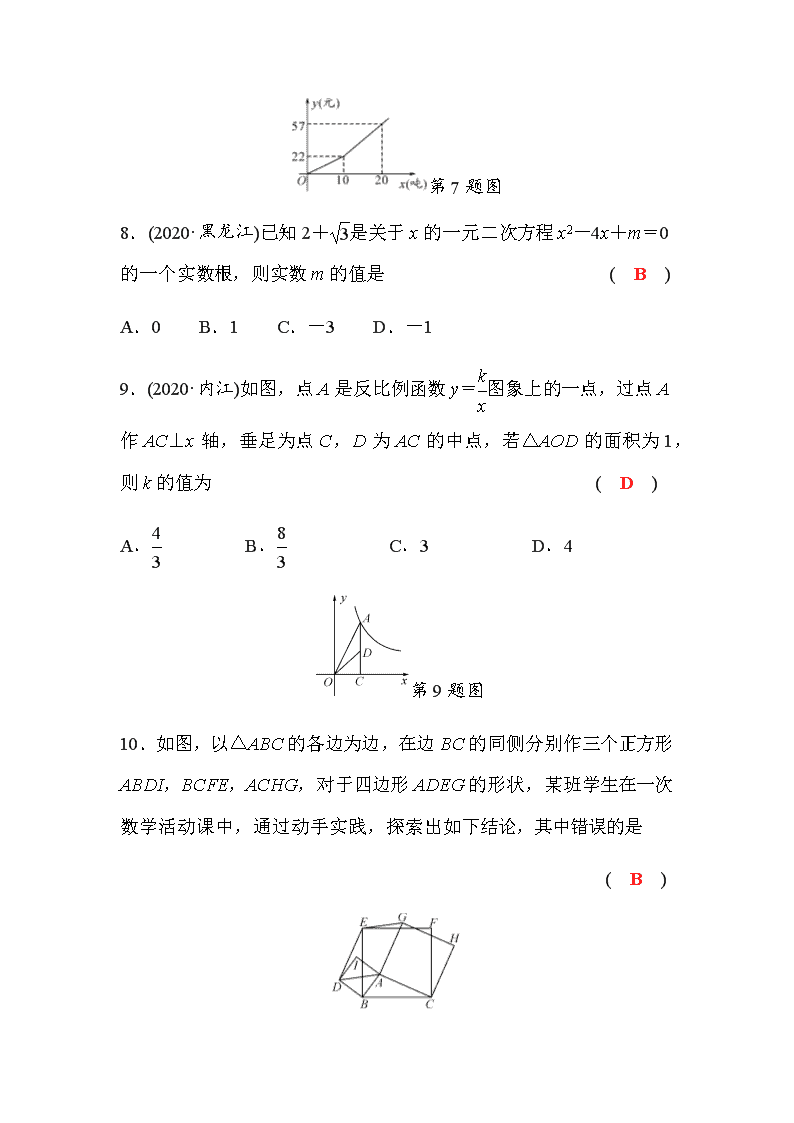
黔东南州、黔南州、黔西南州2021年初中毕业升学考试 数学 模拟卷(三) (考试时间:120分钟 满分:150分) 一、选择题(本大题共10小题,每小题4分,共40分) 1.|2-6|的相反数是 ( A ) A.-4 B.- C. D.4 2.(2020·吉林)国务院总理李克强2020年5月22日在作政府工作报告时说,去年我国农村贫困人口减少11 090 000人,脱贫攻坚取得决定性成就.数据11 090 000用科学记数法表示为 ( B ) A.11.09×106 B.1.109×107 C.1.109×108 D.0.110 9×108 3.如图,直线AB,CD相交于点O,OE平分∠BOD,过点O作OF⊥OE,若∠AOC=42°,则∠BOF的度数为 ( D ) A.48° B.52° C.64° D.69° 第3题图 第4题图 4.(2020·孝感)如图是由5个完全相同的小正方体组成的几何体,则该几何体的左视图是 ( A ) 5.如图,在数轴上有A,B,C,D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A,D两点表示的数分别为-5和6,点E为线段BD的中点,那么中点E表示的数为 ( C ) A.0 B.1 C.2 D.3 6.(2020·重庆)围成下列立体图形的各个面中,每个面都是平的是( A ) 7.为了节约水资源,自来水公司按分段收费标准收费,如图所示反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.按照分段收费标准,小颖家三、四月份分别交水费29元和19.8元,则四月份比三月份节约用水 ( C ) A.2吨 B.2.5吨 C.3吨 D.3.5吨 第7题图 8.(2020·黑龙江)已知2+是关于x的一元二次方程x2-4x+m=0的一个实数根,则实数m的值是 ( B ) A.0 B.1 C.-3 D.-1 9.(2020·内江)如图,点A是反比例函数y=图象上的一点,过点A作AC⊥x轴,垂足为点C,D为AC的中点,若△AOD的面积为1,则k的值为 ( D ) A. B. C.3 D.4 第9题图 10. 如图,以△ABC的各边为边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG,对于四边形ADEG的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是 ( B ) A.若△ABC为任意三角形,则四边形ADEG是平行四边形 B.若∠BAC=90°,则四边形ADEG是矩形 C.若AC=AB,则四边形ADEG是菱形 D.若∠BAC=135°且AC=AB,则四边形ADEG是正方形 二、填空题(本大题共10小题,每小题3分,共30分) 11.(2020·鄂州)因式分解:2m2-12m+18=__2(m-3)2__. 12.当__x=1__时,2x-3和3x-2的值互为相反数. 13.(2020·凉山州)若不等式组恰有四个整数解,则a的取值范围是__-≤a<-__. 14.(2020·内江)在函数y=中,自变量x的取值范围是__x≠2__. 15.如图,将△ABC沿BC边上的中线AD平移到△A′B′C′的位置,已知△ABC的周长为9,阴影部分三角形的周长为6.若AA′=1,则AD等于__3__. 第15题图 第16题图 16.如图,直线a∥c,∠1=∠2,那么直线b,c的位置关系是__b∥c__. 17.如图,在等腰△ABC的两腰AB,BC上分别取点D和E,使DB=DE,此时恰有∠ADE=∠ACB,则∠B的度数是__20°__. 18.对于三个数a,b,c,我们规定用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}==,min{-1,2,3}=-1.如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=__或__. 19.如图,是由6个同样大小的正方体摆成的几何体,如果将最上层的正方体分别移到①号,②号,③号或④号正方体的上面(接触面所有的棱都重合),会得到4种新的几何体,那么所得到的4种几何体的左视图相同的是__①②__. 第19题图 第20题图 20.如图,在边长为2 cm的正六边形ABCDEF中,点P在BC上,则△PEF的面积为__2__cm2. 三、解答题(本大题共6小题,共80分) 21.(14分)学生马小虎计算某整式减去xy+2yz-4xz时,由于粗心,误认为加上此式,得到的结果为3xy-2xz+5yz. (1)试求此题的正确计算结果; (2)若x,y,z满足|x-2|+(y+3)2+=0,则本题的正确结果是什么? 解:(1)依题知某整式为 (3xy-2xz+5yz)-(xy+2yz-4xz) =3xy-2xz+5yz-xy-2yz+4xz =2xy+2xz+3yz, 故正确结果为 (2xy+2xz+3yz)-(xy+2yz-4xz) =2xy+2xz+3yz-xy-2yz+4xz =xy+yz+6xz. (2)∵|x-2|+(y+3)2+=0, ∴x-2=0,y+3=0,6+3z=0, 即x=2,y=-3,z=-2,(1)的计算结果为2×(-3)+(-3)×(-2)+6×2×(-2)=-24. 22.(12分)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB. (1)求∠CAD的度数; (2)延长AC至E,使CE=AC,求证:DA=DE. (1)解:∵在Rt△ABC中, ∵∠ACB=90°,∠B=30°, ∴∠CAB=60°. 又∵AD平分∠CAB, ∴∠CAD=∠CAB=30°,即∠CAD=30°. (2)证明:∵∠ACD+∠ECD=180°, 且∠ACD=90°, ∴∠ECD=90°,∴∠ACD=∠ECD. 在△ACD与△ECD中, ∴△ACD≌△ECD(SAS),∴DA=DE. 23.(12分)某养鸭场有10 000只鸭准备对外出售,从中随机抽取了一部分鸭,根据它们的质量(单位:kg),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题: 图① 图② (1)图①中m的值为______; (2)求统计的这组数据的平均数、众数和中位数; (3)根据规定质量为1.5~1.8 kg的鸭子为“上品”,养鸭场这10 000只鸭子约有多少只“上品”? 解:(1)28. (2)这组数据的平均数为 =1.52(kg), 众数为1.8,中位数为=1.5. (3) 估计这10 000只鸭中,质量为1.5~1.8 kg的约有 10 000×=6 000(只). 答:养鸭场大约有6 000只“上品”鸭子. 24.(14分)某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种新型商品成本为20元/件,第x天销售量为p件,销售单价为q元,经跟踪调查发现,这40天中p与x的关系保持不变,前20天(包含第20天),q与x的关系满足关系式q=30+ax;从第21天到第40天中,q是基础价与浮动价的和,其中基础价保持不变,浮动价与x成反比.且得到了表中的数据. x(天) 10 21 35 q(元/件) 35 45 35 (1)请直接写出a的值为______; (2)从第21天到第40天中,求q与x满足的关系式; (3)若该网店第x天获得的利润y元,并且已知这40天里前20天中y与x的函数关系式为y=-x2+15x+500 ①请直接写出这40天中p与x的关系式为______; ②求这40天里该网店第几天获得的利润最大? 解:(1)0.5. (2)设从第21天到第40天中,q与x满足的关系式为q=b+, 把(21,45)和(35,35)代入得 解得 ∴q=20+. (3)①由题意得[(30+0.5x)-20]·p=-x2+15x+500, ∴p=50-x.故答案为p=50-x; ②当1≤x≤20时,y=-x2+15x+500=-(x-15)2+612.5, 当x=15时,y有最大值是612.5; 当21≤x≤40时,y=(50-x)=-525, ∵y随x的增大而减小, ∴当x=21时,y有最大值,是725, 综上所述,这40天里该网店第21天获得的利润最大. 25.(14分)如图①,等边△ABC边长为6,AD是△ABC的中线,P在线段AD上运动,以CP为一边且在CP左下方作如图所示的等边△CPE,连接BE. (1)求证:AP=BE; (2)如图②,若在BE延长线上取点F,使得 CF=CE, ①当AP为何值时,EF的长为6; ②若△BCE的外心在其内部时,试写出AP的取值范围. 图① 图② (1)证明:∵△ABC和△CPE均为等边三角形, ∴∠ACB=∠PCE=60°,AC=BC,CP=CE, ∴∠ACP+∠DCP=∠DCE+∠PCD=60°, ∴∠ACP=∠BCE. ∵在△ACP和△BCE中, ∴△ACP≌△BCE(SAS).∴BE=AP. (2)如图②所示:过点C作CH⊥BF,垂足为H, ∵AB=AC,AD是BC的中点, ∴∠CAD=∠BAD=∠BAC=30°. ∵由(1)可知△ACP≌△BCE, ∴∠CBE=∠CAD=30°,AP=BE. ∵在Rt△BCH中,∠HBC=30°, ∴HC=BC=3,BH=BC=3, ∵CF=CE,CH⊥EF,∴EH=HF=EF=3, ∴BE=BH-EH=3-3, ∴AP=3-3. (3)当△BCE是锐角三角形时,其外心在其内部.过点C作CG⊥BC,交BF于点G,则BG=4. ∴当BH查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档