2019中考数学压轴题

2019中考数学压轴题

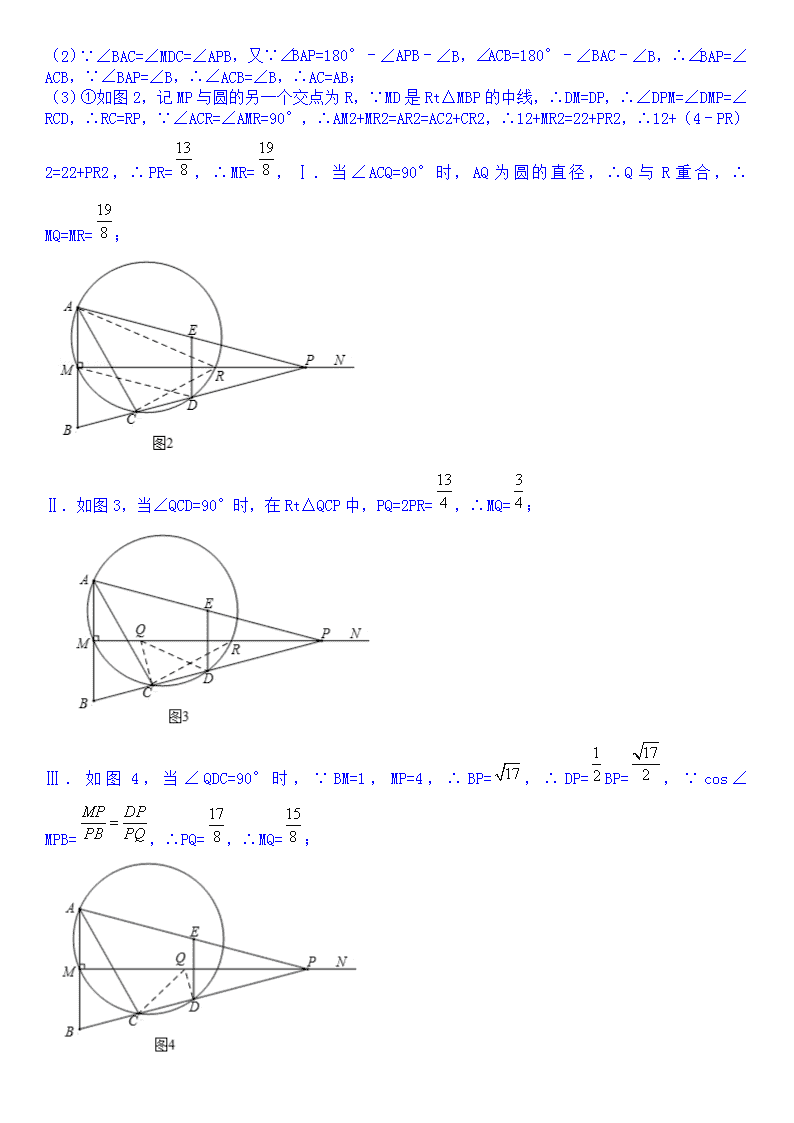
‎2019中考数学压轴题 ‎81．（2017浙江省温州市，第24题，14分）如图，已知线段AB=2，MN⊥AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD上），连结AC，DE．‎ ‎（1）当∠APB=28°时，求∠B和的度数；‎ ‎（2）求证：AC=AB．‎ ‎（3）在点P的运动过程中．‎ ‎①当MP=4时，取四边形ACDE一边的两端点和线段MP上一点Q，若以这三点为顶点的三角形是直角三角形，且Q为锐角顶点，求所有满足条件的MQ的值；‎ ‎②记AP与圆的另一个交点为F，将点F绕点D旋转90°得到点G，当点G恰好落在MN上时，连结AG，CG，DG，EG，直接写出△ACG和△DEG的面积之比．‎ ‎【答案】（1）∠B=76°，=56°；（2）证明见解析；（3）①MQ的值为或或；②．‎ ‎【分析】（1）根据三角形ABP是等腰三角形，可得∠B的度数，再连接MD，根据MD为△PAB的中位线，可得∠MDB=∠APB=28°，进而得到=2∠MDB=56°；‎ ‎（2）根据∠BAP=∠ACB，∠BAP=∠B，即可得到∠ACB=∠B，进而得出AC=AB；‎ ‎（3）①记MP与圆的另一个交点为R，根据AM2+MR2=AR2=AC2+CR2，即可得到PR，MR的值，再根据Q为直角三角形锐角顶点，分四种情况进行讨论：当∠ACQ=90°时，当∠QCD=90°时，当∠QDC=90°时，当∠AEQ=90°时，即可求得MQ的值；‎ ‎②先判定△DEG是等边三角形，再根据GMD=∠GDM，得到GM=GD=1，过C作CH⊥AB于H，由∠BAC=30°可得CH=1=MG，即可得到CG的值，进而得出S△ACG的值，再根据S△DEG的值，即可得到△ACG和△DEG的面积之比．‎ ‎【解析】（1）∵MN⊥AB，AM=BM，∴PA=PB，∴∠PAB=∠B，∵∠APB=28°，∴∠B=76°，如图1，连接MD，∵MD为△PAB的中位线，∴MD∥AP，∴∠MDB=∠APB=28°，∴=2∠MDB=56°；‎ ‎（2）∵∠BAC=∠MDC=∠APB，又∵∠BAP=180°﹣∠APB﹣∠B，∠ACB=180°﹣∠BAC﹣∠B，∴∠BAP=∠ACB，∵∠BAP=∠B，∴∠ACB=∠B，∴AC=AB；‎ ‎（3）①如图2，记MP与圆的另一个交点为R，∵MD是Rt△MBP的中线，∴DM=DP，∴∠DPM=∠DMP=∠RCD，∴RC=RP，∵∠ACR=∠AMR=90°，∴AM2+MR2=AR2=AC2+CR2，∴12+MR2=22+PR2，∴12+（4﹣PR）2=22+PR2，∴PR=，∴MR=，Ⅰ．当∠ACQ=90°时，AQ为圆的直径，∴Q与R重合，∴MQ=MR=；‎ Ⅱ．如图3，当∠QCD=90°时，在Rt△QCP中，PQ=2PR=，∴MQ=；‎ Ⅲ．如图4，当∠QDC=90°时，∵BM=1，MP=4，∴BP=，∴DP=BP=，∵cos∠‎ MPB=，∴PQ=，∴MQ=；‎ Ⅳ．如图5，当∠AEQ=90°时，由对称性可得∠AEQ=∠BDQ=90°，∴MQ=；‎ 综上所述，MQ的值为或或；‎ ‎②△ACG和△DEG的面积之比为．‎ 理由：如图6，∵DM∥AF，∴DF=AM=DE=1，又由对称性可得GE=GD，∴△DEG是等边三角形，∴∠EDF=90°﹣60°=30°，∴∠DEF=75°=∠MDE，∴∠GDM=75°﹣60°=15°，∴∠GMD=∠PGD﹣∠GDM=15°，∴GMD=∠GDM，∴GM=GD=1，过C作CH⊥AB于H，由∠BAC=30°可得 CH=AC=AB=1=MG，AH=，∴CG=MH=﹣1，∴S△ACG=CG×CH=，∵S△DEG=，∴S△AS△DEG =．‎ 点睛：本题属于圆的综合题，主要考查了等腰三角形的性质，等边三角形的判定与性质，三角形中位线定理，勾股定理，圆周角定理以及解直角三角形的综合应用，解决问题的关键是作辅助线构造直角三角形以及等边三角形，运用旋转的性质以及含30°角的直角三角形的性质进行计算求解，解题时注意分类思想的运用．‎ 考点：圆的综合题；旋转的性质；动点型；分类讨论；压轴题．‎ ‎82．（2017湖北省咸宁市，第23题，10分）定义：‎ 数学活动课上，李老师给出如下定义：如果一个三角形有一边上的中线等于这条边的一半，那么称这个三角形为“智慧三角形”．‎ 理解：‎ ‎（1）如图1，已知A、B是⊙O上两点，请在圆上找出满足条件的点C，使△ABC为“智慧三角形”（画出点C的位置，保留作图痕迹）；‎ ‎（2）如图2，在正方形ABCD中，E是BC的中点，F是CD上一点，且CF=CD，试判断△AEF是否为“智慧三角形”，并说明理由；‎ 运用：‎ ‎（3）如图3，在平面直角坐标系xOy中，⊙O的半径为1，点Q是直线y=3上的一点，若在⊙O上存在一点P，使得△OPQ为“智慧三角形”，当其面积取得最小值时，直接写出此时点P的坐标．‎ ‎【答案】（1）作图见解析；（2）△AEF是“智慧三角形”；（3）P的坐标（﹣，），（，）．‎ ‎【分析】（1）连结AO并且延长交圆于C1，连结BO并且延长交圆于C2，即可求解；‎ ‎（2）设正方形的边长为‎4a，表示出DF=CF以及EC、BE的长，然后根据勾股定理列式表示出AF2、EF2、AE2，再根据勾股定理逆定理判定△AEF是直角三角形，由直角三角形的性质可得△AEF为“智慧三角形”；‎ ‎（3）根据“智慧三角形”的定义可得△‎ OPQ为直角三角形，根据题意可得一条直角边为1，当斜边最短时，另一条直角边最短，则面积取得最小值，由垂线段最短可得斜边最短为3，根据勾股定理可求另一条直角边，再根据三角形面积可求斜边的高，即点P的横坐标，再根据勾股定理可求点P的纵坐标，从而求解．‎ ‎【解析】（1）如图1所示：‎ ‎（2）△AEF是否为“智慧三角形”，理由如下：设正方形的边长为‎4a，∵E是DC的中点，∴DE=CE=‎2a，∵BC：FC=4：1，∴FC=a，BF=‎4a﹣a=‎3a，在Rt△ADE中，AE2=（‎4a）2+（‎2a）2=‎20a2，在Rt△ECF中，EF2=（‎2a）2+a2=‎5a2，在Rt△ABF中，AF2=（‎4a）2+（‎3a）2=‎25a2，∴AE2+EF2=AF2，∴△AEF是直角三角形，∵斜边AF上的中线等于AF的一半，∴△AEF为“智慧三角形”；‎ ‎（3）如图3所示，由“智慧三角形”的定义可得△OPQ为直角三角形，根据题意可得一条直角边为1，当斜边最短时，另一条直角边最短，则面积取得最小值，由垂线段最短可得斜边最短为3，由勾股定理可得PQ= =，PM=1×÷3=，由勾股定理可求得OM= =，故点P的坐标（﹣，），（，）．‎ ‎ ‎ 点睛：本题考查了圆的综合题，正方形的性质，勾股定理的应用，勾股定理逆定理的应用，用正方形的边长表示出△AEF的各边的平方，熟练掌握“智慧三角形”的定义是解题的关键．‎ 考点：圆的综合题；新定义；探究型；最值问题；阅读型；压轴题．‎ ‎83．（2017湖南省湘潭市，第26题，10分）如图，动点M在以O为圆心，AB为直径的半圆弧上运动（点M不与点A、B 及的中点F 重合），连接OM．过点M 作ME⊥AB于点E，以BE为边在半圆同侧作正方形BCDE，过点M作⊙O的切线交射线DC于点N，连接BM、BN．‎ ‎（1）探究：如图一，当动点M在上运动时；‎ ‎①判断△OEM∽△MDN是否成立？请说明理由；‎ ‎②设，k是否为定值？若是，求出该定值，若不是，请说明理由；‎ ‎③设∠MBN=α，α是否为定值？若是，求出该定值，若不是，请说明理由；‎ ‎（2）拓展：如图二，当动点M 在上运动时；‎ 分别判断（1）中的三个结论是否保持不变？如有变化，请直接写出正确的结论．（均不必说明理由）‎ ‎【答案】（1）①成立；②k值为定值1；③设∠MBN=α，α为定值45°；（2）不变．‎ ‎【分析】（1）①由正方形的性质得出BE=BC，∠EBC=∠CDE=∠BCD=∠BED=90°，由切线的性质和直角三角形的性质证出∠EOM=∠DMN，即可得出△OEM∽△MDN；‎ ‎②作BG⊥MN于G，则BG∥OM，∠BGN=∠BGM=90°，由平行线的性质和等腰三角形的性质得出∠OBM=∠GBM，由AAS证明△BME≌△BMG，得出EM=GM，BE=BG，证出BG=BC，由HL证明Rt△BGN≌Rt△BCN，得出GN=CN，证出EM+NC=GM+NC=MN，即可得出结论；‎ ‎③由全等三角形的性质得出∠EBM=∠GBM，∠GBN=∠CBN，求出∠MBN=∠EBC=45°即可；‎ ‎（2）（1）中的三个结论保持不变；解法同（1）．‎ ‎【解析】（1）①△OEM∽△MDN成立，理由如下：‎ ‎∵四边形BCDE是正方形，∴BE=BC，∠EBC=∠CDE=∠BCD=∠BED=90°，∴∠EOM+∠EMO=90°，∵MN是⊙O的切线，∴MN⊥OM，∴∠OMN=90°，∴∠DMN+∠EMO=90°，∴∠EOM=∠DMN，∴△OEM∽△MDN；‎ ‎②k值为定值1；理由如下：‎ 作BG⊥MN于G，如图一所示：‎ 则BG∥OM，∠BGN=∠BGM=90°，∴∠OMB=∠GBM，∵OB=OM，∴∠OBM=∠OMB，∴∠OBM=∠GBM，在△BME和△BMG中，∵∠OBM=∠GBM，∠BED=∠BGM=90°，BM=BM，∴△BME≌△BMG（AAS），∴EM=GM，BE=BG，∴BG=BC，在Rt△BGN和Rt△BCN中，∵BN=BN，BG=BC，∴Rt△BGN≌Rt△BCN（HL），∴GN=CN，∴EM+NC=GM+NC=MN，∴k===1；‎ ‎③设∠MBN=α，α为定值45°；理由如下：‎ ‎∵△BME≌△BMG，Rt△BGN≌Rt△BCN，∴∠EBM=∠GBM，∠GBN=∠CBN，∴∠MBN=∠EBC=45°，即α=45°；‎ ‎（2）（1）中的三个结论保持不变；理由同（1），作BG⊥MN于G，如图二所示．‎ 点睛：本题是圆的综合题目，考查了正方形的性质、切线的性质、全等三角形的判定与性质、直角三角形的性质等知识；本题综合性强，有一定难度，证明三角形全等是解决问题的关键．‎ 考点：圆的综合题；定值问题；探究型；动点型；压轴题．‎ ‎84．（2017陕西省，第25题，12分）问题提出 ‎（1）如图①，△ABC是等边三角形，AB=12，若点O是△ABC的内心，则OA的长为 ；‎ 问题探究 ‎（2）如图②，在矩形ABCD中，AB=12，AD=18，如果点P是AD边上一点，且AP=3，那么BC边上是否存在一点Q，使得线段PQ将矩形ABCD的面积平分？若存在，求出PQ的长；若不存在，请说明理由．‎ 问题解决 ‎（3）某城市街角有一草坪，草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成，如图③所示．管理员王师傅在M处的水管上安装了一喷灌龙头，以后，他想只用喷灌龙头来给这块草坪浇水，并且在用喷灌龙头浇水时，既要能确保草坪的每个角落都能浇上水，又能节约用水，于是，他让喷灌龙头的转角正好等于∠AMB（即每次喷灌时喷灌龙头由MA转到MB，然后再转回，这样往复喷灌．）同时，再合理设计好喷灌龙头喷水的射程就可以了．‎ 如图③，已测出AB=‎24m，MB=‎10m，△AMB的面积为‎96m2‎；过弦AB的中点D作DE⊥AB交于点E，又测得DE=‎8m．‎ 请你根据以上信息，帮助王师傅计算喷灌龙头的射程至少多少米时，才能实现他的想法？为什么？（结果保留根号或精确到‎0.01米）‎ ‎【答案】（1）；（2）PQ=；（3）喷灌龙头的射程至少为‎19.71米．‎ ‎【分析】（1）构建Rt△AOD中，利用cos∠OAD=cos30°=，可得OA的长；‎ ‎（2）经过矩形对角线交点的直线将矩形面积平分，根据此结论作出PQ，利用勾股定理进行计算即可；‎ ‎（3）如图3，作辅助线，先确定圆心和半径，根据勾股定理计算半径：‎ 在Rt△AOD中，由勾股定理解得：r=13根据三角形面积计算高MN的长，证明△ADC∽△ANM，列比例式求DC的长，确定点O在△AMB内部，利用勾股定理计算OM，则最大距离FM的长可利用相加得出结论．‎ ‎【解析】（1）如图1，过O作OD⊥AC于D，则AD=AC=×12=6，∵O是内心，△ABC是等边三角形，∴∠OAD=∠BAC=×60°=30°，在Rt△AOD中，cos∠OAD=cos30°=，∴OA=6÷=，故答案为：；‎ ‎（2）存在，如图2，连接AC、BD交于点O，连接PO并延长交BC于Q，则线段PQ将矩形ABCD的面积平分，∵点O为矩形ABCD的对称中心，∴CQ=AP=3，过P作PM⊥BC于点，则PM=AB=12，MQ=18﹣3﹣3=12，由勾股定理得：PQ= ==；‎ ‎（3）如图3，作射线ED交AM于点C．∵AD=DB，ED⊥AB，是劣弧，∴所在圆的圆心在射线DC上，假设圆心为O，半径为r，连接OA，则OA=r，OD=r﹣8，AD=AB=12，在Rt△AOD中，r2=122+（r﹣8）2，解得：r=13，∴OD=5，过点M作MN⊥AB，垂足为N，∵S△ABM=96，AB=24，∴AB•MN=96，×24×MN=96，∴MN=8，NB=6，AN=18，∵CD∥MN，∴△ADC∽△ANM，∴，∴，∴DC=，∴OD＜CD，∴点O在△AMB内部，∴连接MO并延长交于点F，则MF为草坪上的点到M点的最大距离，∵在上任取一点异于点F的点G，连接GO，GM，∴MF=OM+OF=OM+OG＞MG，即MF＞MG，过O作OH⊥MN，垂足为H，则OH=DN=6，MH=3，∴OM===，∴MF=OM+r=+13≈19.71（米）．‎ 答：喷灌龙头的射程至少为‎19.71米．‎ 点睛：本题是圆的综合题，考查了三角形相似的性质和判定、勾股定理、等边三角形的性质及内心的定义、特殊的三角函数值、矩形的性质等知识，明确在特殊的四边形中将面积平分的直线一定过对角线的交点，本题的第三问比较复杂，辅助线的作出是关键，根据三角形的三角关系确定其最大射程为MF．‎ 考点：圆的综合题；最值问题；存在型；阅读型；压轴题．‎ ‎85．（2017黑龙江省哈尔滨市，第26题，10分）已知：AB是⊙O的弦，点C是的中点，连接OB、OC，OC交AB于点D．‎ ‎（1）如图1，求证：AD=BD；‎ ‎（2）如图2，过点B作⊙O的切线交OC的延长线于点M，点P是上一点，连接AP、BP，求证：∠APB﹣∠OMB=90°；‎ ‎（3）如图3，在（2）的条件下，连接DP、MP，延长MP交⊙O于点Q，若MQ=6DP，sin∠ABO=，求的值．‎ ‎【答案】（1）证明见解析；（2）证明见解析；（3）．‎ ‎【分析】（1）如图1，连接OA，利用垂径定理和圆周角定理可得结论；‎ ‎（2）如图2，延长BO交⊙O于点T，连接PT，由圆周角定理可得∠BPT=90°，易得∠APT=∠APB﹣∠BPT=∠APB﹣90°，利用切线的性质定理和垂径定理可得∠ABO=∠OMB，等量代换可得∠ABO=∠APT，易得结论；‎ ‎（3）如图3，连接MA，利用垂直平分线的性质可得MA=MB，易得∠MAB=∠MBA，作∠PMG=∠AMB，在射线MG上截取MN=MP，连接PN，BN，易得△APM≌△BNM，由全等三角形的性质可得AP=BN，∠MAP=∠MBN，延长PD至点K，使DK=DP，连接AK、BK，易得四边形APBK是平行四边形，由平行四边形的性质和平行线的性质可得∠PAB=∠ABK，∠APB+∠PBK=180°，由（2）得∠APB﹣（90°﹣∠MBA）=90°，易得∠NBP=∠KBP，可得△PBN≌△PBK，PN=2PH，利用三角函数的定义可得sin∠PMH=，sin∠ABO=，设DP=‎3a，则PM=‎5a，可得结果．‎ ‎【解析】（1）证明：如图1，连接OA，∵C是的中点，∴，∴∠AOC=∠BOC，∵OA=OB，∴OD⊥AB，AD=BD；‎ ‎（2）证明：如图2，延长BO交⊙O于点T，连接PT．∵BT是⊙O的直径，∴∠BPT=90°，∴∠APT=∠APB﹣∠BPT=∠APB﹣90°，∵BM是⊙O的切线，∴OB⊥BM，又∠OBA+∠MBA=90°，∴∠ABO=∠OMB．又∠ABO=∠APT，∴∠APB﹣90°=∠OMB，∴∠APB﹣∠OMB=90°；‎ ‎（3）解：如图3，连接MA，∵MO垂直平分AB，∴MA=MB，∴∠MAB=∠MBA，作∠PMG=∠AMB，在射线MG上截取MN=MP，连接PN，BN，则∠AMP=∠BMN，∴△APM≌△BNM，∴AP=BN，∠MAP=∠MBN，延长PD至点K，使DK=DP，连接AK、BK，∴四边形APBK是平行四边形；‎ AP∥BK，∴∠PAB=∠ABK，∠APB+∠PBK=180°，由（2）得∠APB﹣（90°﹣∠MBA）=90°，∴∠APB+∠MBA=180°，∴∠PBK=∠MBA，∴∠MBP=∠ABK=∠PAB，∴∠MAP=∠PBA=∠MBN，∴∠NBP=∠KBP，∵PB=PB，∴△PBN≌△PBK，∴PN=PK=2PD，过点M作MH⊥PN于点H，∴PN=2PH，∴PH=DP，∠PMH=∠ABO，∵sin∠PMH=，sin∠ABO=，∴=，∴=，设DP=‎3a，则PM=‎5a，∴MQ=6DP=‎18a，∴=．‎ 点睛：本题主要考查了垂径定理，圆周角定理，全等三角形的判定与性质定理，三角函数的定义等相关知识，作出恰当的辅助线构建全等三角形是解答此题的关键．‎ 考点：圆的综合题；压轴题．‎ ‎86．（2017山东省莱芜市，第23题，10分）已知AB是⊙O的直径，C是圆上一点，∠BAC的平分线交⊙O于点D，过D作DE⊥AC交AC的延长线于点E，如图①．‎ ‎（1）求证：DE是⊙O的切线；‎ ‎（2）若AB=10，AC=6，求BD的长；‎ ‎（3）如图②，若F是OA中点，FG⊥OA交直线DE于点G，若FG=，tan∠BAD=，求⊙O的半径．‎ ‎【答案】（1）证明见解析；（2）；（3）4．‎ ‎【分析】（1）欲证明DE是⊙O的切线，只要证明OD⊥DE；‎ ‎（2）首先证明OD⊥BC，在Rt△BDN中，利用勾股定理计算即可；‎ ‎（3）如图②中，设FG与AD交于点H，根据题意，设AB=5x，AD=4x，则AF=x，想办法用x表示线段FH、GH，根据FH+GH=，列出方程即可解决问题；‎ ‎【解析】（1）证明：如图①中，连接OD．∵OA=OD，∴∠OAD=∠ODA，∵AD平分∠BAC，∴∠OAD=∠DAE，∴∠ODA=∠DAE，∴OD∥AE，∴∠ODE+∠AED=180°，∵∠AED=90°，∴∠ODE=90°，∴OD⊥DE，∴DE是⊙O的切线．‎ ‎（2）如图①中，连接BC，交OD于点N，∵AB是直径，∴∠BCA=90°，∵OD∥AE，O是AB的中点，∴ON∥AC，且ON=AC，∴∠ONB=90°，且ON=3，则BN=4，ND=2，∴BD==．‎ ‎（3）如图②中，设FG与AD交于点H，根据题意，设AB=5x，AD=4x，则AF=x，FH=AF•tan∠BAD=‎ x•=x，AH== =，HD=AD﹣AH=4x﹣=，由（1）可知，∠HDG+∠ODA=90°，在Rt△HFA中，∠FAH+∠FHA=90°，∵∠OAD=∠ODA，∠FHA=∠DHG，∴∠DHG=∠HDG，∴GH=GD，过点G作GM⊥HD，交HD于点M，∴MH=MD，∴HM=HD=×=，∵∠FAH+∠AHF=90°，∠MHG+∠HGM=90°，∴∠FAH=∠HGM，在Rt△HGM中，HG===，∵FH+GH=，∴+=，解得x=，∴此圆的半径为×=4．‎ 点睛：本题考查圆综合题、切线的判定、垂径定理、勾股定理、锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．‎ 考点：圆的综合题．‎ ‎87．（2017黑龙江省大庆市，第27题，9分）如图，四边形ABCD内接于圆O，∠BAD=90°，AC为直径，过点A作圆O的切线交CB的延长线于点E，过AC的三等分点F（靠近点C）作CE的平行线交AB于点G，连结CG．‎ ‎（1）求证：AB=CD；‎ ‎（2）求证：CD2=BE•BC；‎ ‎（3）当CG=，BE=时，求CD的长．‎ ‎【答案】（1）证明见解析；（2）证明见解析；（3）．‎ ‎【分析】（1）根据三个角是直角的四边形是矩形证明四边形ABCD是矩形，可得结论；‎ ‎（2）证明△ABE∽△CBA，列比例式可得结论；‎ ‎（3）根据F是AC的三等分点得：AG=2BG，设BG=x，则AG=2x，代入（2）的结论解出x的值，可得CD的长．‎ ‎【解析】（1）∵AC为⊙O的直径，∴∠ABC=∠ADC=90°，∵∠BAD=90°，∴四边形ABCD是矩形，∴AB=CD；‎ ‎（2）∵AE为⊙O的切线，∴AE⊥AC，∴∠EAB+∠BAC=90°，∵∠BAC+∠ACB=90°，∴∠EAB=∠ACB，∵∠ABC=90°，∴△ABE∽△CBA，∴，∴AB2=BE•BC，由（1）知：AB=CD，∴CD2=BE•BC；‎ ‎（3）∵F是AC的三等分点，∴AF=2FC，∵FG∥BE，∴△AFG∽△ACB，∴ =2，设BG=x，则AG=2x，∴AB=3x，在Rt△BCG中，CG=，∴BC2=（）2﹣x2，BC=，由（2）得：AB2=BE•BC，（3x）2=，4x4+x2﹣3=0，（x2+1）（4x2﹣3）=0，x=±，∵x＞0，∴x=，∴CD=AB=3x=．‎ 点睛：本题是圆和四边形的综合题，难度适中，考查了矩形的性质和判定、平行相似的判定、三角形相似的性质、圆周角定理、切线的性质、勾股定理等知识，注意第2和3问都应用了上一问的结论，与方程相结合，熟练掌握一元高次方程的解法．‎ 考点：圆的综合题；压轴题．‎ ‎88．（2016四川省达州市）如图，已知AB为半圆O的直径，C为半圆O上一点，连接AC，BC，过点O作OD⊥AC于点D，过点A作半圆O的切线交OD的延长线于点E，连接BD并延长交AE于点F．‎ ‎（1）求证：AE•BC=AD•AB；‎ ‎（2）若半圆O的直径为10，sin∠BAC=，求AF的长．‎ ‎【答案】（1）证明见解析；（2）．‎ ‎【分析】（1）只要证明△EAD∽△ABC即可解决问题．‎ ‎（2）作DM⊥AB于M，利用DM∥AE，得，求出DM、BM即可解决问题．‎ ‎【解析】（1）∵AB为半圆O的直径，∴∠C=90°，∵OD⊥AC，∴∠CAB+∠AOE=90°，∠ADE=∠C=90°，∵AE是切线，∴OA⊥AE，∴∠E+∠AOE=90°，∴∠E=∠CAB，∴△EAD∽△ABC，∴AE：AB=AD：BC，∴AE•BC=AD•AB．‎ ‎（2）作DM⊥AB于M，∵半圆O的直径为10，sin∠BAC=，∴BC=AB•sin∠BAC=6，∴AC==8，∵OE⊥AC，∴AD=AC=4，OD=BC=3，∵sin∠MAD==，∴DM=，AM===，BM=AB﹣AM=，∵DM∥AE，∴，∴AF=．‎ 考点：相似三角形的判定与性质；勾股定理；切线的性质；锐角三角函数的定义．‎ ‎89．（2016山西省）请阅读下列材料，并完成相应的任务：‎ 阿基米德折弦定理 阿基米德（archimedes，公元前287﹣公元前212年，古希腊）是有史以来最伟大的数学家之一，他与牛顿、高斯并成为三大数学王子．‎ 阿拉伯Al﹣Binmi（973﹣1050年）的译文中保存了阿基米德折弦定理的内容，苏联在1964年根据Al﹣Binmi译本出版了俄文版《阿基米德全集》，第一题就是阿基米德折弦定理．‎ 阿基米德折弦定理：如图1，AB和BC是⊙O的两条弦（即折线ABC是圆的一条折弦），BC＞AB，M是的中点，则从M向BC所作垂线的垂足D是折弦ABC的中点，即CD=AB+BD．下面是运用“截长法”证明CD=AB+BD的部分证明过程．证明：如图2，在CB上截取CG=AB，连接MA，MB，MC和MG．‎ ‎∵M是的中点，∴MA=MC．‎ ‎…‎ 任务：‎ ‎（1）请按照上面的证明思路，写出该证明的剩余部分；‎ ‎（2）填空：如图3，已知等边△ABC内接于⊙O，AB=2，D为上一点，∠ABD=45°，AE⊥BD于点E，则△BDC的周长是 ．‎ ‎【答案】（1）证明见解析；（2）．‎ ‎【分析】（1）首先证明△MBA≌△MGC（SAS），进而得出MB=MG，再利用等腰三角形的性质得出BD=GD，即可得出答案；‎ ‎（2）首先证明△ABF≌ACD（SAS），进而得出AF=AD，以及CD+DE=BE，进而求出DE的长即可得出答案．‎ ‎（2）解：如图3，截取BF=CD，连接AF，AD，CD，由题意可得：AB=AC，∠ABF=∠ACD，在△ABF和△ACD中，∵AB=AC，∠ABF=∠ACD，BF=DC，∴△ABF≌ACD（SAS），∴AF=AD，∵AE⊥BD，∴FE=DE，则CD+DE=BE，∵∠ABD=45°，∴BE==，则△BDC的周长是．故答案为：．‎ 考点：三角形的外接圆与外心；等边三角形的性质；阅读型；和差倍分．‎ ‎90．（2016广东省茂名市）如图，在△ABC中，∠C=90°，D、F是AB边上的两点，以DF为直径的⊙O与BC相交于点E，连接EF，过F作FG⊥BC于点G，其中∠OFE=∠A．‎ ‎（1）求证：BC是⊙O的切线；‎ ‎（2）若sinB=，⊙O的半径为r，求△EHG的面积（用含r的代数式表示）．‎ ‎【答案】（1）证明见解析；（2）．‎ ‎【分析】（1）首先连接OE，由在△ABC中，∠C=90°，FG⊥BC，可得FG∥AC，又由∠OFE=∠A，易得EF平分∠BFG，继而证得OE∥FG，证得OE⊥BC，则可得BC是⊙O的切线；‎ ‎（2）由在△OBE中，sinB=‎ ‎，⊙O的半径为r，可求得OB，BE的长，然后由在△BFG中，求得BG，FG的长，则可求得EG的长，易证得△EGH∽△FGE，然后由相似三角形面积比等于相似比的平方，求得答案．‎ ‎【解析】（1）证明：连接OE，∵在△ABC中，∠C=90°，FG⊥BC，∴∠BGF=∠C=90°，∴FG∥AC，∴∠OFG=∠A，∴∠OFE=∠OFG，∴∠OFE=∠EFG，∵OE=OF，∴∠OFE=∠OEF，∴∠OEF=∠EFG，∴OE∥FG，∴OE⊥BC，∴BC是⊙O的切线；‎ ‎（2）解：∵在Rt△OBE中，sinB=，⊙O的半径为r，∴OB=r，BE=r，∴BF=OB+OF=r，∴FG=BF•sinB=r，∴BG==r，∴EG=BG﹣BE=r，∴S△FGE=EG•FG=，EG：FG=1：2，∵BC是切线，∴∠GEH=∠EFG，∵∠EGH=∠FGE，∴△EGH∽△FGE，∴==，∴S△EHG=S△FGE=．‎ 考点：切线的判定．‎ ‎91．（2016内蒙古呼和浩特市）如图，已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连接FB，FC．‎ ‎（1）求证：∠FBC=∠FCB；‎ ‎（2）已知FA•FD=12，若AB是△ABC外接圆的直径，FA=2，求CD的长．‎ ‎【答案】（1）证明见解析；（2）．‎ ‎【分析】（1）由圆内接四边形的性质和邻补角关系证出∠FBC=∠CAD，再由角平分线和对顶角相等得出∠FAB=∠CAD，由圆周角定理得出∠FAB=∠FCB，即可得出结论；‎ ‎（2）由（1）得：∠FBC=∠FCB，由圆周角定理得出∠FAB=∠FBC，由公共角∠BFA=∠BFD，证出△AFB∽△BFD，得出对应边成比例求出BF，得出FD、AD的长，由圆周角定理得出∠BFA=∠BCA=90°，由三角函数求出∠FBA=30°，再由三角函数求出CD的长即可．‎ ‎【解析】（1）证明：∵四边形AFBC内接于圆，∴∠FBC+∠FAC=180°，∵∠CAD+∠FAC=180°，∴∠FBC=∠CAD，∵AD是△ABC的外角∠EAC的平分线，∴∠EAD=∠CAD，∵∠EAD=∠FAB，∴∠FAB=∠CAD，又∵∠FAB=∠FCB，∴∠FBC=∠FCB；‎ ‎（2）解：由（1）得：∠FBC=∠FCB，又∵∠FCB=∠FAB，∴∠FAB=∠FBC，∵∠BFA=∠BFD，∴△AFB∽△BFD，∴，∴=FA•FD=12，∴BF=，∵FA=2，∴FD=6，AD=4，∵AB为圆的直径，∴∠BFA=∠BCA=90°，∴tan∠FBA===，∴∠FBA=30°，又∵∠FDB=∠FBA=30°，∴CD=AD•cos30°=4×=．‎ 考点：相似三角形的判定与性质；三角形的外接圆与外心．‎ ‎92．（2016内蒙古巴彦淖尔市）如图，在△ABC中，∠C=90°，∠ABC的平分线交AC于点E，过点E作BE的垂线交AB于点F，⊙O是△BEF的外接圆．‎ ‎（1）求证：AC是⊙O的切线；‎ ‎（2）过点E作EH⊥AB，垂足为H，求证：CD=HF；‎ ‎（3）若CD=1，EH=3，求BF及AF长．‎ ‎【答案】（1）证明见解析；（2）证明见解析；（3）BF=10，AF=．‎ ‎【分析】（1）连接OE，由于BE是角平分线，则有∠CBE=∠OBE；而OB=OE，就有∠OBE=∠OEB，等量代换有∠OEB=∠CBE，那么利用内错角相等，两直线平行，可得OE∥BC；又∠C=90°，所以∠AEO=90°，即AC是⊙O的切线；‎ ‎（2）连结DE，先根据AAS证明△CDE≌△HFE，再由全等三角形的对应边相等即可得出CD=HF．‎ ‎（3）先证得△EHF∽△BEF，根据相似三角形的性质求得BF=10，进而根据直角三角形斜边中线的性质求得OE=5，进一步求得OH，然后解直角三角形即可求得OA，得出AF．‎ ‎【解析】（1）如图，连接OE．‎ ‎∵BE⊥EF，∴∠BEF=90°，∴BF是圆O的直径．‎ ‎∵BE平分∠ABC，∴∠CBE=∠OBE，∵OB=OE，∴∠OBE=∠OEB，∴∠OEB=∠CBE，∴OE∥BC，∴∠AEO=∠C=90°，∴AC是⊙O的切线；‎ ‎（2）如图，连结DE．‎ ‎∵∠CBE=∠OBE，EC⊥BC于C，EH⊥AB于H，∴EC=EH．‎ ‎∵∠CDE+∠BDE=180°，∠HFE+∠BDE=180°，∴∠CDE=∠HFE．‎ 在△CDE与△HFE中，∵∠CDE=∠HFE，∠C=∠EHF，EC=EH，∴△CDE≌△HFE（AAS），∴CD=HF．‎ ‎（3）由（2）得CD=HF，又CD=1，∴HF=1，在Rt△HFE中，EF==，∵EF⊥BE，∴∠BEF=90°，∴∠EHF=∠BEF=90°，∵∠EFH=∠BFE，∴△EHF∽△BEF，∴，即，∴BF=10，∴OE=BF=5，OH=5﹣1=4，∴Rt△OHE中，cos∠EOA=，∴Rt△EOA中，cos∠EOA==，∴‎ ‎=，∴OA=，∴AF=﹣5=．‎ 考点：切线的判定；三角形的外接圆与外心；相似三角形的判定与性质．‎ ‎93．（2016四川省宜宾市）如图1，在△APE中，∠PAE=90°，PO是△APE的角平分线，以O为圆心，OA为半径作圆交AE于点G．‎ ‎（1）求证：直线PE是⊙O的切线；‎ ‎（2）在图2中，设PE与⊙O相切于点H，连结AH，点D是⊙O的劣弧上一点，过点D作⊙O的切线，交PA于点B，交PE于点C，已知△PBC的周长为4，tan∠EAH=，求EH的长．‎ ‎【答案】（1）证明见解析；（2）．‎ ‎【分析】（1）作OH⊥PE，由PO是∠APE的角平分线，得到∠APO=∠EPO，判断出△PAO≌△PHO，得到OH=OA，用“圆心到直线的距离等于半径”来得出直线PE是⊙O的切线；‎ ‎（2）先利用切线的性质和△PBC的周长为4求出PA=2，再用三角函数求出OA，AG，然后用三角形相似，得到EH=2EG，AE=2EH，用勾股定理求出EG，最后用切割线定理即可．‎ ‎【解析】（1）如图1，作OH⊥PE，∴∠OHP=90°，∵∠PAE=90，∴∠OHP=∠OAP，∵PO是∠APE的角平分线，∴∠APO=∠EPO，在△PAO和△PHO中，∵∠OHP=∠OAP，∠OPH=∠OPA，OP=OP，∴△PAO≌△PHO，∴OH=OA，∵OA是⊙O的半径，∴OH是⊙O的半径，∵OH⊥PE，∴直线PE是⊙O的切线．‎ ‎（2）如图2，连接GH，∵BC，PA，PB是⊙O的切线，∴DB=DA，DC=CH，∵△PBC的周长为4，∴PB+PC+BC=4，∴PB+PC+DB+DC=4，∴PB+AB+PC+CH=4，∴PA+PH=4，∵PA，PH是⊙O的切线，∴PA=PH，∴PA=2，由（1）得，△PAO≌△PHO，∴∠OFA=90°，∴∠EAH+∠AOP=90°，∵∠OAP=90°，∴∠AOP+∠APO=90°，∴∠APO=∠EAH，‎ ‎∵tan∠EAH=，∴tan∠APO==，∴OA=PA=1，∴AG=2，∵∠AHG=90°，∵tan∠EAH==，∵△EGH∽△EHA，∴==‎ ‎，∴EH=2EG，AE=2EH，∴AE=4EG，∵AE=EG+AG，∴EG+AG=4EG，∴EG=AG=，∵EH是⊙O的切线，EGA是⊙O的割线，∴=EG×EA=EG×（EG+AG）==，∴EH=．‎ 考点：切线的判定与性质．‎ ‎94．（2016江西省）如图，AB是⊙O的直径，点P是弦AC上一动点（不与A，C重合），过点P作PE⊥AB，垂足为E，射线EP交于点F，交过点C的切线于点D．‎ ‎（1）求证：DC=DP；‎ ‎（2）若∠CAB=30°，当F是的中点时，判断以A，O，C，F为顶点的四边形是什么特殊四边形？说明理由．‎ ‎【答案】（1）证明见解析；（2）以A，O，C，F为顶点的四边形是菱形．‎ ‎【分析】（1）连接BC、OC，利用圆周角定理和切线的性质可得∠B=∠ACD，由PE⊥AB，易得∠APE=∠DPC=∠B，等量代换可得∠DPC=∠ACD，可证得结论；‎ ‎（2）由∠CAB=30°易得△OBC为等边三角形，可得∠AOC=120°，由F是的中点，易得△AOF与△COF均为等边三角形，可得AF=AO=OC=CF，易得以A，O，C，F为顶点的四边形是菱形．‎ ‎【解析】（1）连接BC、OC，∵AB是⊙O的直径，∴∠OCD=90°，∴∠OCA+∠OCB=90°，∵∠OCA=∠OAC，∠B=∠OCB，∴∠OAC+∠B=90°，∵CD为切线，∴∠OCD=90°，∴∠OCA+∠ACD=90°，∴∠B=∠ACD，∵PE⊥AB，∴∠APE=∠DPC=∠B，∴∠DPC=∠ACD，∴AP=DC；‎ ‎（2）以A，O，C，F为顶点的四边形是菱形．理由如下：‎ ‎∵∠CAB=30°，∴∠B=60°，∴△OBC为等边三角形，∴∠AOC=120°，连接OF，AF，∵F是的中点，∴∠AOF=∠COF=60°，∴△AOF与△COF均为等边三角形，∴AF=AO=OC=CF，∴四边形OACF为菱形．‎ 考点：切线的性质；垂径定理．‎ ‎95．（2016江苏省南京市）如图，O是△ABC内一点，⊙O与BC相交于F、G两点，且与AB、AC分别相切于点D、E，DE∥BC，连接DF、EG．‎ ‎（1）求证：AB=AC．‎ ‎（2）已知AB=10，BC=12，求四边形DFGE是矩形时⊙O的半径．‎ ‎【答案】（1）证明见解析；（2）．‎ ‎【分析】（1）由切线长定理可知AD=AE，易得∠ADE=∠AED，因为DE∥BC，由平行线的性质得∠ADE=∠B，∠AED=∠C，可得∠B=∠C，易得AB=AC；‎ ‎（2）如图，连接AO，交DE于点M，延长AO交BC于点N，连接OE、DG，设⊙O半径为r，由△AOD∽△ABN得，得到AD=r，再由△GBD∽△ABN得，列出方程即可解决问题．‎ ‎【解析】（1）证明：∵AD、AE是⊙O的切线，∴AD=AE，∴∠ADE=∠AED，∵DE∥BC，∴∠ADE=∠B，∠AED=∠C，∴∠B=∠C，∴AB=AC；‎ ‎（2）解：如图，连接AO，交DE于点M，延长AO交BC于点N，连接OE、DG，设⊙O半径为r，‎ ‎∵四边形DFGE是矩形，∴∠DFG=90°，∴DG是⊙O直径，∵⊙O与AB、AC分别相切于点D、E，∴OD⊥AB，OE⊥AC，∵OD=OE，OE⊥AC，∵OD=OE，∴AN平分∠BAC，∵AB=AC，∴AN⊥BC，BN=‎ BC=6，在RT△ABN中，AN===8，∵OD⊥AB，AN⊥BC，∴∠ADO=∠ANB=90°，∵∠OAD=∠BAN，∴△AOD∽△ABN，∴，即，∴AD=r，∴BD=AB﹣AD=10﹣r，∵OD⊥AB，∴∠GDB=∠ANB=90°，∵∠B=∠B，∴△GBD∽△ABN，∴，即，∴r=，∴四边形DFGE是矩形时⊙O的半径为．‎ 考点：切线的性质；矩形的性质．‎ ‎96．（2016江苏省扬州市）如图1，以△ABC的边AB为直径的⊙O交边BC于点E，过点E作⊙O的切线交AC于点D，且ED⊥AC．‎ ‎（1）试判断△ABC的形状，并说明理由；‎ ‎（2）如图2，若线段AB、DE的延长线交于点F，∠C=75°，CD=，求⊙O的半径和BF的长．‎ ‎【答案】（1）△ABC是等腰三角形；（2）BF=，⊙O的半径为2．‎ ‎【分析】（1）连接OE，根据切线性质得OE⊥DE，与已知中的ED⊥AC得平行，由此得∠1=∠C，再根据同圆的半径相等得∠1=∠B，可得出三角形为等腰三角形；‎ ‎（2）通过作辅助线构建矩形OGDE，再设与半径有关系的边OG=x，通过AB=AC列等量关系式，可求得结论．‎ ‎【解析】（1）△ABC是等腰三角形，理由是：‎ 如图1，连接OE，∵DE是⊙O的切线，∴OE⊥DE，∵ED⊥AC，∴AC∥OE，∴∠1=∠C，∵OB=OE，∴∠1=∠B，∴∠B=∠C，∴△ABC是等腰三角形；‎ ‎（2）如图2，过点O作OG⊥AC，垂足为G，则得四边形OGDE是矩形，∵△ABC是等腰三角形，∴∠B=∠C=75°，∴∠A=180°﹣75°﹣75°=30°，设OG=x，则OA=OB=OE=2x，AG=x，∴DG=0E=2x，根据AC=AB得：，x=1，∴0E=OB=2，在直角△OEF中，∠EOF=∠A=30°，cos30=，OF==2÷=，∴BF=，⊙O的半径为2．‎ 考点：切线的性质；探究型．‎ ‎97．（2016湖北省十堰市）如图1，AB为半圆O的直径，D为BA的延长线上一点，DC为半圆O的切线，切点为C．‎ ‎（1）求证：∠ACD=∠B；‎ ‎（2）如图2，∠BDC的平分线分别交AC，BC于点E，F；‎ ‎①求tan∠CFE的值；‎ ‎②若AC=3，BC=4，求CE的长．‎ ‎【答案】（1）证明见解析；（2）①1；②．‎ ‎【分析】（1）利用等角的余角相等即可证明．‎ ‎（2）①只要证明∠CEF=∠CFE即可．‎ ‎②由△DCA∽△DBC，得，设DC=3k，DB=4k，由=DA•DB，得，由此求出DC，DB，再由△DCE∽△DBF，得，设EC=CF=x，列出方程即可解决问题．‎ ‎【解析】（1）证明：如图1中，连接OC．∵OA=OC，∴∠1=∠2，∵CD是⊙O切线，∴OC⊥CD，∴∠DCO=90°，∴∠3+∠2=90°，∵AB是直径，∴∠1+∠B=90°，∴∠3=∠B；‎ ‎（2）解：①∵∠CEF=∠ECD+∠CDE，∠CFE=∠B+∠FDB，∵∠CDE=∠FDB，∠ECD=∠B，∴∠CEF=∠CFE，∵∠ECF=90°，∴∠CEF=∠CFE=45°，∴tan∠CFE=tan45°=1；‎ ‎②在RT△ABC中，∵AC=3，BC=4，∴AB==5，∵∠CDA=∠BDC，∠DCA=∠B，∴△DCA∽△DBC，∴，设DC=3k，DB=4k，∵=DA•DB，∴，∴k=，∴CD=，DB=，∵∠CDE=∠BDF，∠DCE=∠B，∴△DCE∽△DBF，∴，设EC=CF=x，∴，∴x=，∴CE=．‎ 考点：切线的性质；压轴题．‎ ‎98．（2016湖北省武汉市）如图，点C在以AB为直径的⊙O上，AD与过点C的切线垂直，垂足为点D，AD交⊙O于点E．‎ ‎（1）求证：AC平分∠DAB；‎ ‎（2）连接BE交AC于点F，若cos∠CAD=，求的值．‎ ‎【答案】（1）证明见解析；（2）．‎ ‎【分析】（1）连接OC，根据切线的性质和已知求出OC∥AD，求出∠OCA=∠CAO=∠DAC，即可得出答案；‎ ‎（2）连接BE、BC、OC，BE交AC于F交OC于H，根据cos∠CAD==，设AD=‎4a，AC=‎5a，则DC=EH=HB=‎3a，根据cos∠CAB==，求出AB、BC，再根据勾股定理求出CH，由此即可解决问题；‎ ‎【解析】（1）证明：连接OC，∵CD是⊙O的切线，∴CD⊥OC，又∵CD⊥AD，∴AD∥OC，∴∠CAD=∠ACO，∵OA=OC，∴∠CAO=∠ACO，∴∠CAD=∠CAO，即AC平分∠DAB；‎ ‎（2）解：连接BE、BC、OC，BE交AC于F交OC于H．∵AB是直径，∴∠AEB=∠DEH=∠D=∠DCH=90°，∴四边形DEHC是矩形，∴∠EHC=90°即OC⊥EB，∴DC=EH=HB，DE=HC，∵cos∠CAD==，设AD=‎4a，AC=‎5a，则DC=EH=HB=‎3a，∵cos∠CAB==，∴AB=a，BC=a，在RT△‎ CHB中，CH==a，∴DE=CH=a，AE==a，∵EF∥CD，∴==．‎ 考点：切线的性质．‎