- 2021-04-23 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2018届一轮复习人教A版导数与函数的单调性学案
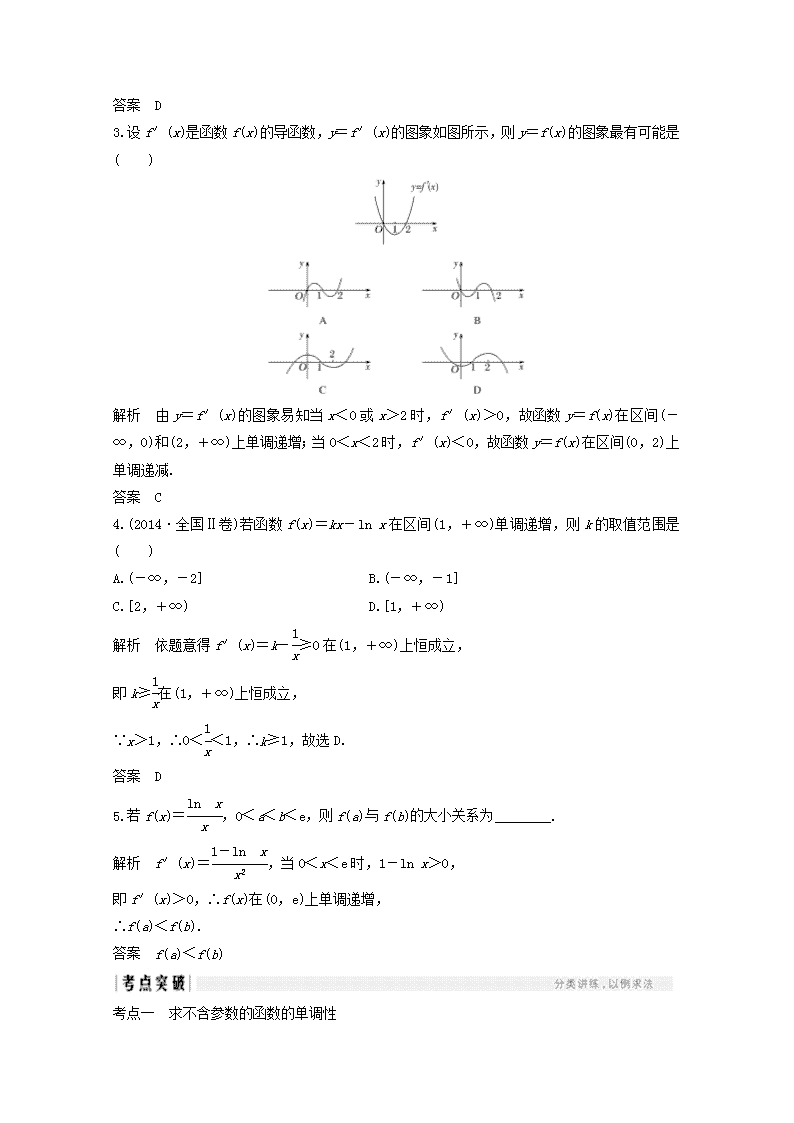
第 2 讲 导数与函数的单调性 最新考纲 了解函数的单调性与导数的关系;能利用导数研究函数的单调性,会求函数的单 调区间(其中多项式函数不超过三次). 知 识 梳 理 1.函数的单调性与导数的关系 已知函数 f(x)在某个区间内可导, (1)如果 f′(x)>0,那么函数 y=f(x)在这个区间内单调递增; (2)如果 f′(x)<0,那么函数 y=f(x)在这个区间内单调递减. 2.利用导数求函数单调区间的基本步骤是: (1)确定函数 f(x)的定义域; (2)求导数 f′(x); (3)由 f′(x)>0(或<0)解出相应的 x 的取值范围.当 f′(x)>0 时,f(x)在相应的区间内是 单调递增函数;当 f′(x)<0 时,f(x)在相应的区间内是单调递减函数. 一般需要通过列表,写出函数的单调区间. 3.已知单调性求解参数范围的步骤为: (1)对含参数的函数 f(x)求导,得到 f′(x); (2)若函数 f(x)在[a,b]上单调递增,则 f′(x)≥0 恒成立;若函数 f(x)在[a,b]上单调递 减,则 f′(x)≤0 恒成立,得到关于参数的不等式,解出参数范围; (3)验证参数范围中取等号时,是否恒有 f′(x)=0.若 f′(x)=0 恒成立,则函数 f(x)在(a, b)上为常数函数,舍去此参数值. 诊 断 自 测 1.判断正误(在括号内打“√”或“×”) (1)若函数 f(x)在(a,b)内单调递增,那么一定有 f′(x)>0.( ) (2)如果函数 f(x)在某个区间内恒有 f′(x)=0,则 f(x)在此区间内没有单调性.( ) (3)f′(x)>0 是 f(x)为增函数的充要条件.( ) 解析 (1)f(x)在(a,b)内单调递增,则有 f′(x)≥0. (2)f′(x)>0 是 f(x)为增函数的充分不必要条件. 答案 (1)× (2)√ (3)× 2.函数 f(x)=ex-x 的单调递增区间是( ) A.(-∞,1] B.[1,+∞) C.(-∞,0] D.(0,+∞) 解析 令 f′(x)=ex-1>0 得 x>0,所以 f(x)的递增区间为(0,+∞). 答案 D 3.设 f′(x)是函数 f(x)的导函数,y=f′(x)的图象如图所示,则 y=f(x)的图象最有可能是 ( ) 解析 由 y=f′(x)的图象易知当 x<0 或 x>2 时,f′(x)>0,故函数 y=f(x)在区间(- ∞,0)和(2,+∞)上单调递增;当 0<x<2 时,f′(x)<0,故函数 y=f(x)在区间(0,2)上 单调递减. 答案 C 4.(2014·全国Ⅱ卷)若函数 f(x)=kx-ln x 在区间(1,+∞)单调递增,则 k 的取值范围是 ( ) A.(-∞,-2] B.(-∞,-1] C.[2,+∞) D.[1,+∞) 解析 依题意得 f′(x)=k- 1 x≥0 在(1,+∞)上恒成立, 即 k≥ 1 x在(1,+∞)上恒成立, ∵x>1,∴0< 1 x<1,∴k≥1,故选 D. 答案 D 5.若 f(x)= ln x x ,0<a<b<e,则 f(a)与 f(b)的大小关系为________. 解析 f′(x)= 1-ln x x2 ,当 0<x<e 时,1-ln x>0, 即 f′(x)>0,∴f(x)在(0,e)上单调递增, ∴f(a)<f(b). 答案 f(a)<f(b) 考点一 求不含参数的函数的单调性 【例 1】 已知函数 f(x)=ax3+x2(a∈R)在 x=- 4 3处取得极值. (1)确定 a 的值; (2)若 g(x)=f(x)ex,讨论 g(x)的单调性. 解 (1)对 f(x)求导得 f′(x)=3ax2+2x, 因为 f(x)在 x=- 4 3处取得极值,所以 f′(- 4 3 )=0, 所以 3a· 16 9 +2·(- 4 3 )= 16a 3 - 8 3=0,解得 a= 1 2. (2)由(1)得 g(x)=(1 2x3+x2)ex, 故 g′(x)=(3 2x2+2x)ex+(1 2x3+x2)ex =(1 2x3+ 5 2x2+2x)ex = 1 2x(x+1)(x+4)ex. 令 g′(x)=0, 解得 x=0,x=-1 或 x=-4. 当 x<-4 时,g′(x)<0,故 g(x)为减函数; 当-4查看更多