- 2021-04-23 发布 |
- 37.5 KB |
- 3页


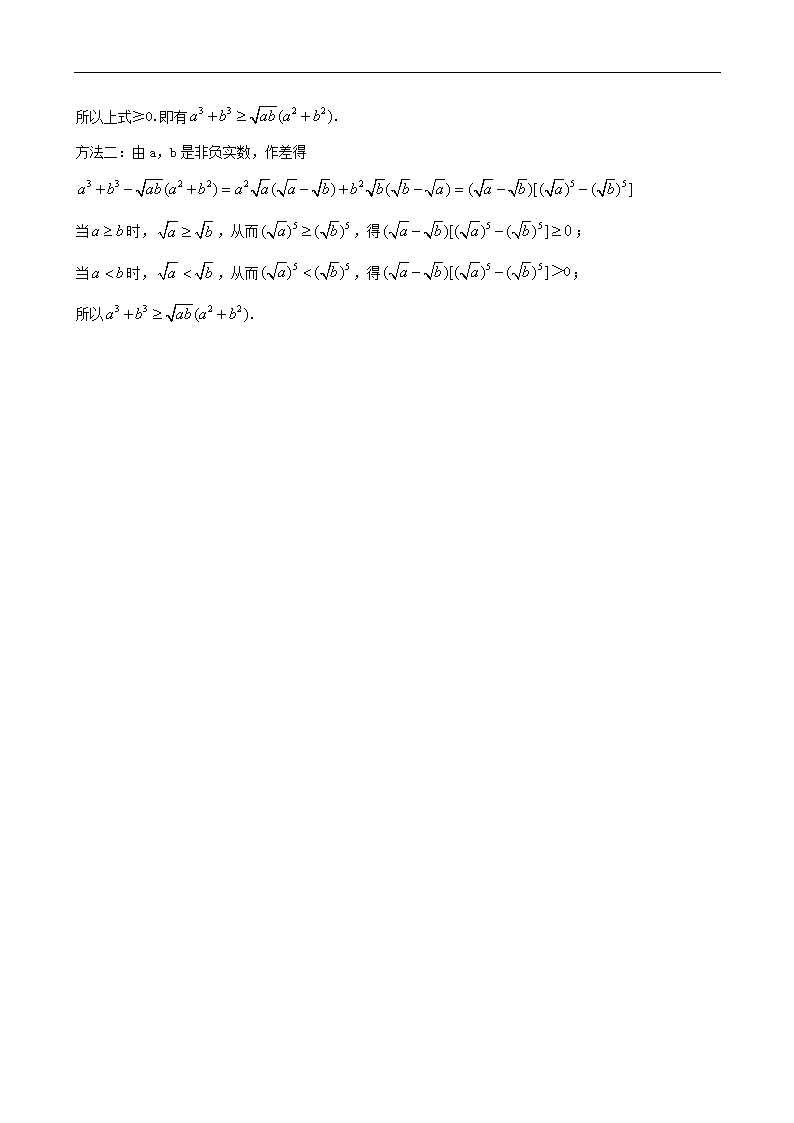
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
新课标版高考数学复习题库考点33 不等式选讲
考点33 不等式选讲 1(2010·辽宁高考理科·T24)已知均为正数,证明:, 并确定为何值时,等号成立. 【命题立意】本题考查了不等式的性质,考查了均值不等式. 【思路点拨】把,分别用均值不等式,相加后,再用均值不等式. 【规范解答】证法一: ∵ …………………………① , ∴……………………② ……………………③ ∴原不等式成立. 当且仅当a=b=c时,①式和②式等号成立,当且仅当时,③式等号成立. 即当a=b=c=时原式等号成立. 证法二:∵a,b,c都是正数,由基本不等式得 ∴………………………………① 同理………………………………② ∴ …………………………………………③ ∴原不等式成立 当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,时,③式等号成立. 即当a=b=c=时原式等号成立. 2.(2010·福建高考理科·T21)已知函数()=. (Ⅰ)若不等式()≤3的解集为{-1≤≤5},求实数的值; (Ⅱ)在(Ⅰ)的条件下,若()+()≥对一切实数恒成立,求实数的取值范围. 【命题立意】本题主要考查绝对值的意义、绝对值不等式等基础知识,考查运算求解能力. 【思路点拨】(1)由公式求解含绝对值的不等式,进而求出a的值,(2)令g(x)=f(x)+f(x+5),结合g(x)的图象求解. 【规范解答】(1) ,对应系数得; (2)令g(x)=f(x)+f(x+5),结合的图象,所以,故. 3.(2010·江苏高考·T21(D))选修4-5:不等式选讲 设a,b是非负实数,求证:. 【命题立意】 本题主要考查证明不等式的基本方法,考查推理论证的能力. 【思路点拨】利用作差法证明. 【规范解答】方法一: 因为实数a,b≥0,, 所以上式≥0.即有. 方法二:由a,b是非负实数,作差得 当时,,从而,得; 当时,,从而,得>0; 所以. 查看更多