- 2021-04-23 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文卷·2017届四川省成都市高三一诊考试(2016
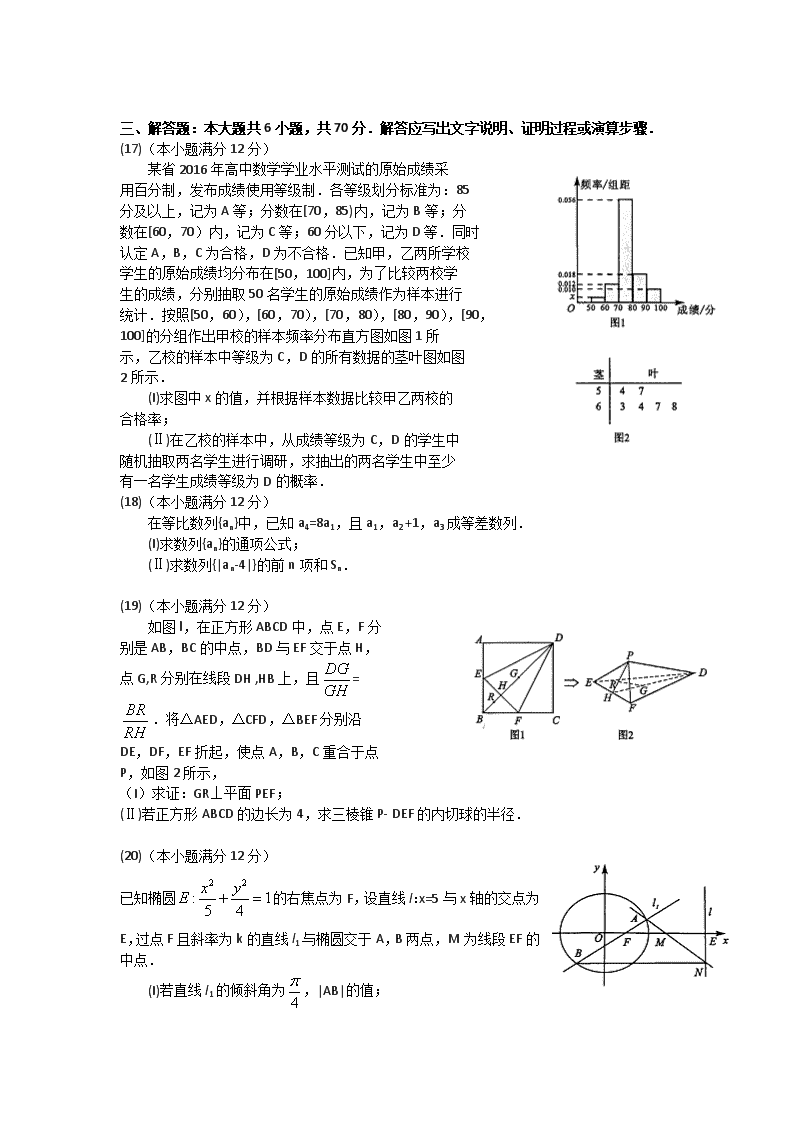
成都市2014级高中毕业班第一次诊断性检测 数学(文科) 本试卷分选择题和非选择题两部分。第I卷(选择题)1至2页,第Ⅱ卷(非选择题)2至4页,共4页,满分150分,考试时间120分钟。 第I卷(选择题,共60分) 一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合U=R,A={x|(x+l) (x -2)<0},则 (A)(一∞,-1) (2,+∞) (B)[-l,2] (C)(一∞,-1] [2,+∞) (D)(一1,2) (2)命题“若a>b,则a+c>b+c”的逆命题是 (A)若a>b,则a+c≤b+c (B)若a+c≤b+c,则a≤b (C)若a+c>b+c,则a>b (D)若a≤b,则a+c≤b+c (3)双曲线的离心率为 (A)4 (B) (C) (D) (4)已知α为锐角,且sinα=詈,则cos(π+α)= (A)一 (B) (C) — (D) (5)执行如图所示的程序框图,如果输出的结果为0,那么输入的x为 (A) (B) -1或1 (C) –l (D)l (6)已知x与y之间的一组数据: 若y关于x的线性回归方程为=2.lx-1.25,则m的值为 (A)l (B)0. 85 (C)0.7 (D)0.5 (7)已知定义在R上的奇函数f(x)满足f(x+3)=f(x),且当 x∈[0,)时,f(x)= 一x3.则f()= (A) - (B) (C) - (D) (8)如图,格纸上小正方形的边长为1,粗实线画出的是某四棱锥 的三视图,则该四棱锥的所有棱中,最长的棱的长度为 (A) (B) (C)5 (D) 3 (9)将函数f(x)=sin2x+cos2x图象上所有点向右平移个单位长度,得到函数g (x)的图象,则g(x)图象的一个对称中心是 (A)(,0) (B)( ,0) (C)(一,0) (D)(,0) (10)在直三棱柱ABC-A1BlC1中,平面α与棱AB,AC,A1C1,A1B1分别交于点E,F,G, H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α上平面BCFE.其中正确的命题有 (A)①② (B)②③ (C)①③ (D)①②③ (11)已知A,B是圆O:x2+y2=4上的两个动点,若M是线段AB的中点,则的值为 (A)3 (B) 2 (C)2 (D) -3 (12)已知曲线C1:y2 =tx (y>0,t>0)在点M(,2)处的切线与曲线C2:y=ex+l+1也相切,则t的值为 (A) 4e2 (B) 4e (C) (D) 第Ⅱ卷(非选择题,共90分) 二、填空题:本大题共4小题,每小题5分,共20分. (13)复数z=(i为虚数单位)的虚部为 . (14)我国南北朝时代的数学家祖暅提出体积的计算原理 (祖暅原理):“幂势既同,则积不容异”.“势”即是高, “幂”是面积.意思是:如果两等高的几何体在同高处截 得两几何体的截面积恒等,那么这两个几何体的体积 相等,类比祖暅原理,如图所示,在平面直角坐标系中, 图1是一个形状不规则的封闭图形,图2是一个矩形, 且当实数t取[0,4]上的任意值时,直线y=t被图1和图2所截得的线段长始终相 等,则图1的面积为 . (15)若实数x,y满足约束条件,则3x-y的最大值为 (16)已知△ABC中,AC=,BC=,△ABC的面积为,若线段BA的延长线上存在点D,使∠BDC =,则CD = . 三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. (17)(本小题满分12分) 某省2016年高中数学学业水平测试的原始成绩采 用百分制,发布成绩使用等级制.各等级划分标准为:85 分及以上,记为A等;分数在[70,85)内,记为B等;分 数在[60,70)内,记为C等;60分以下,记为D等.同时 认定A,B,C为合格,D为不合格.已知甲,乙两所学校 学生的原始成绩均分布在[50,100]内,为了比较两校学 生的成绩,分别抽取50名学生的原始成绩作为样本进行 统计.按照[50,60),[60,70),[70,80),[80,90),[90, 100]的分组作出甲校的样本频率分布直方图如图1所 示,乙校的样本中等级为C,D的所有数据的茎叶图如图 2所示. (I)求图中x的值,并根据样本数据比较甲乙两校的 合格率; (Ⅱ)在乙校的样本中,从成绩等级为C,D的学生中 随机抽取两名学生进行调研,求抽出的两名学生中至少 有一名学生成绩等级为D的概率. (18)(本小题满分12分) 在等比数列{an}中,已知a4=8a1,且a1,a2 +1,a3成等差数列. (I)求数列{an}的通项公式; (Ⅱ)求数列{|an-4|}的前n项和Sn. (19)(本小题满分12分) 如图l,在正方形ABCD中,点E,F分 别是AB,BC的中点,BD与EF交于点H, 点G,R分别在线段DH ,HB上,且= .将△AED,△CFD,△BEF分别沿 DE,DF,EF折起,使点A,B,C重合于点 P,如图2所示, (I)求证:GR⊥平面PEF; (Ⅱ)若正方形ABCD的边长为4,求三棱锥P- DEF的内切球的半径. (20)(本小题满分12分) 已知椭圆的右焦点为F,设直线l:x=5与x轴的交点为E,过点F且斜率为k的直线l1与椭圆交于A,B两点,M为线段EF的中点. (I)若直线l1的倾斜角为,|AB|的值; (Ⅱ)设直线AM交直线l于点N,证明:直线BN⊥l. (21)(本小题满分12分) 已知函数f(x)=xlnx+(l-k)x+k,k∈R. (I)当k=l时,求函数f(x)的单调区间; (Ⅱ)当x>1时,求使不等式f(x)>0恒成立的最大整数k的值. 请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一题计分. (22)(本小题满分10分)选修4-4:坐标系与参数方程 在平面直角坐标系xOy中,倾斜角为α(α≠)的直线l的参数方程为 (t为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρcosxθ - 4sinθ=0. (I)写出直线l的普通方程和曲线C的直角坐标方程; (Ⅱ)已知点P(1,0).若点M的极坐标为(1,),直线l经过点M且与曲线C相交于A,B两点,设线段AB的中点为Q,求|PQ|的值. (23)(本小题满分10分)选修4-5:不等式选讲 已知函数f(x)=x +1+ |3 -x|,x≥-1. (I)求不等式f(x)≤6的解集; (Ⅱ)若f(x)的最小值为n,正数a,b满足2nab =a+2b,求2a+b的最小值. 查看更多