专题11 数学文化（第02期）-备战2017高考高三数学（文）全国各地一模金卷分项解析版

专题11 数学文化（第02期）-备战2017高考高三数学（文）全国各地一模金卷分项解析版

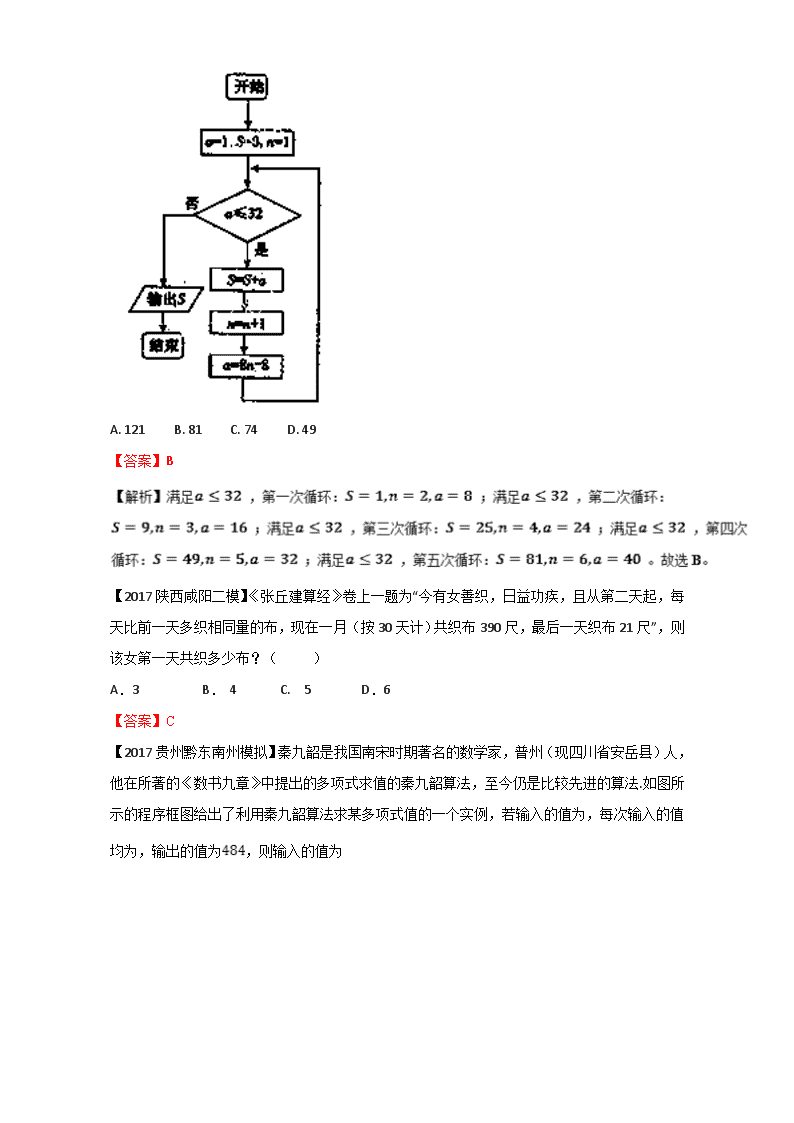
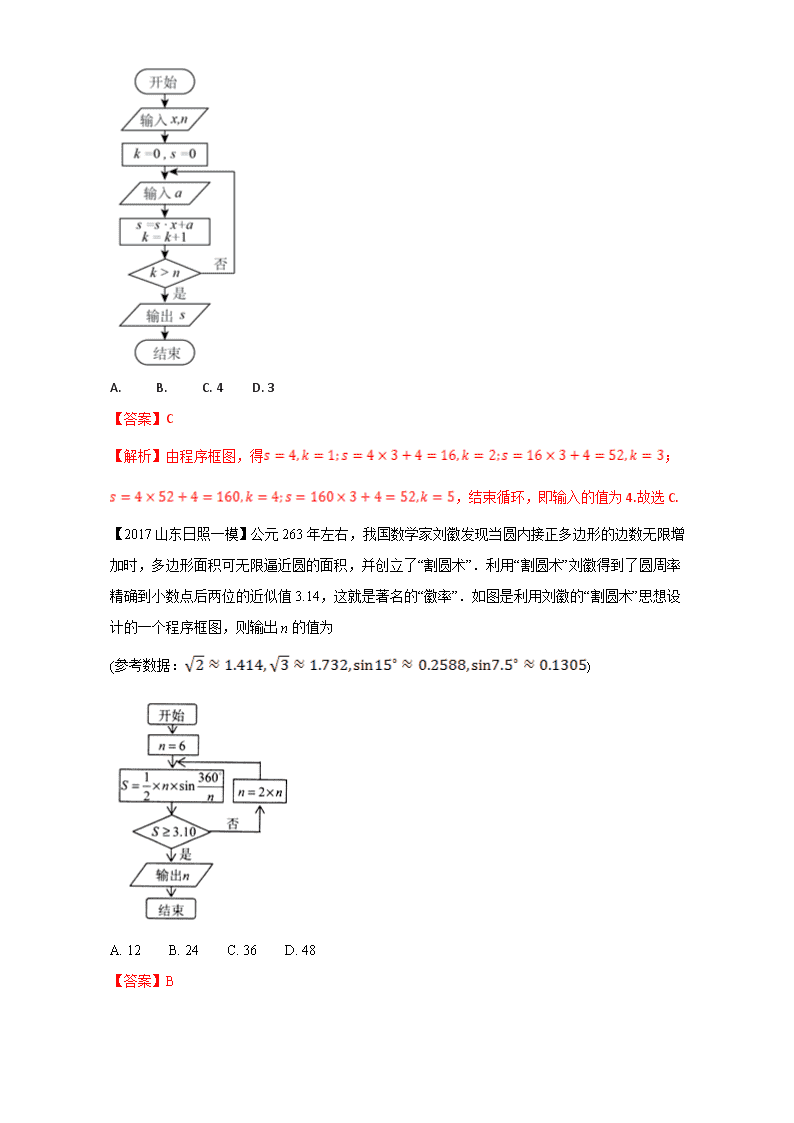
一、选择题 ‎【2017重庆一调】我国古代数学名著《数书九章》有“米谷粒分”题：粮仓开仓收粮，有人送来米2000石，验得米内夹谷，抽样取米一把，数得300粒内夹谷36粒，则这批米内夹谷约为（ ）‎ A. 1760石 B. 200石 C. 300石 D. 240石 ‎【答案】D ‎【2017江西七校联考】欧阳修《卖炭翁》中写到：（翁）乃取一葫芦置于地，以钱覆其口，徐以杓酌油沥之，自钱孔入，而钱不湿．可见“行行出状元”，卖油翁的技艺让人叹为观止．若铜钱是直径为圆，中间有边长为的正方形孔，若你随机向铜钱上滴一滴油，则油（油滴的大小忽略不计）正好落入孔中的概率为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】圆的面积为 ，正方形的面积为 ，所以概率为 ，故选A.‎ ‎【2017福建莆田质检】我国古代数学著作《孙子算经》中有如下问题：“今有方物一束，外周一匝有三十二枚，问积几何？”设每层外周枚数为，如图是解决该问题的程序框图，则输出的结果为（ ）‎ A. 121 B. 81 C. 74 D. 49‎ ‎【答案】B ‎【2017陕西咸阳二模】《张丘建算经》卷上一题为“今有女善织，日益功疾，且从第二天起，每天比前一天多织相同量的布，现在一月（按30天计）共织布390尺，最后一天织布21尺”，则该女第一天共织多少布？（ ）‎ A．3 B． 4 C. 5 D．6‎ ‎【答案】C ‎【2017贵州黔东南州模拟】秦九韶是我国南宋时期著名的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入的值为，每次输入的值均为，输出的值为，则输入的值为 A. B. C. 4 D. 3‎ ‎【答案】C ‎【解析】由程序框图，得；‎ ，结束循环，即输入的值为4.故选C.‎ ‎【2017山东日照一模】公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出n的值为 ‎(参考数据：)‎ A. 12 B. 24 C. 36 D. 48‎ ‎【答案】B ‎【点睛】本题考查数学文化与程序框图，属中档题；数学文化是高考新增内容，程序框图是第年高考的必考内容，掌握循环程序的运行方法，框图以赋值框和条件框为主，按照框图箭线方向和每个框的指令要求运行，注意条件框的要求是否满足，运行程序时要准确.‎ ‎【2017广东广州一模】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥为鳖臑, ⊥平面, ，,三棱锥的四个顶点都在球的球面上, 则球的表面积为 A. B. C. D. ‎ ‎【答案】C 二、填空题 ‎【2017湖北黄冈3月质检】我国古代数学名著《张邱健算经》有“分钱问题”如下：“今有与人钱，初一人与三钱，次一人与四钱，次一人与五钱，以次与之，转多一钱。与讫，还敛聚与均分之，人得一百钱，问人几何？”意思是：“将钱分给若干人，第一人给3钱，第二人给4钱，第三人给5钱，以此类推，每人比前一人多给1钱，分完后，再把钱收回平均分给各人，结果每人分得100钱，问有多少人？”则分钱问题中的人数为 ．‎ ‎【答案】195‎ ‎【解析】试题分析：本题考查等差数列相关知识，设人数为，依题意有，解得，所以共有人. ‎ ‎【2017湖北黄冈3月质检】关于圆周率，数学发展史上出现过许多很有创意的求法，如著名的蒲丰实验和查理斯实验.受其启发，我们也可以通过设计下面的实验来估计的值：先请200名同学，每人随机写下一个都小于1的正实数对，再统计两数能与1构成钝角三角形三边的数对的个数；最后再根据统计数来估计的值，假如统计结果是，那么可以估计 ．（用分数表示）‎ ‎【答案】（或3.12）‎ ‎【点睛】‎ ‎(1)当试验的结果构成的区域为长度、面积、体积等时，应考虑使用几何概型求解．‎ ‎(2)利用几何概型求概率时，关键是试验的全部结果构成的区域和事件发生的区域的寻找，有时需要设出变量，在坐标系中表示所需要的区域．‎ ‎（3）几何概型有两个特点：一是无限性，二是等可能性．基本事件可以抽象为点，尽管这些点是无限的，但它们所占据的区域都是有限的，因此可用“比例解法”求解几何概型的概率．‎