- 2021-04-23 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年高考数学(理)二轮复习讲练测 专题13 算法、推理与证明、复数(讲)(解析版)
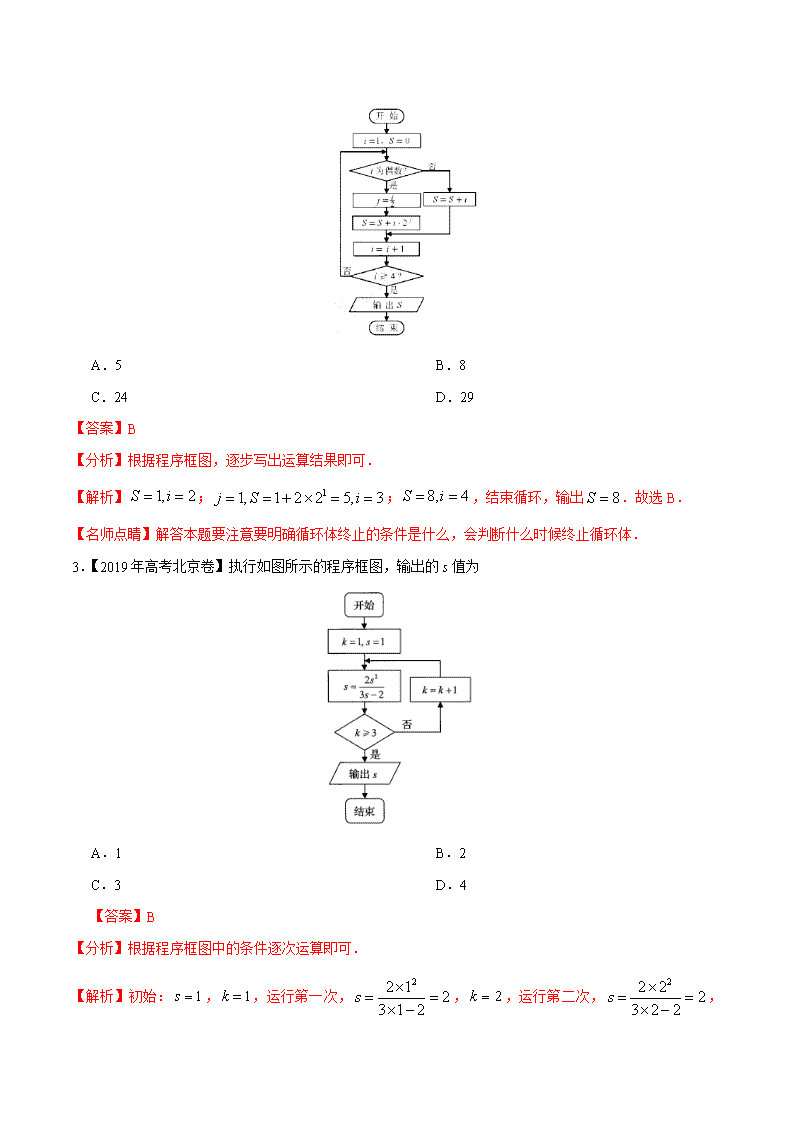
专题13 算法、推理与证明、复数 1.【2019年高考全国Ⅰ卷】如图是求的程序框图,图中空白框中应填入 A. B. C. D. 【答案】A 【分析】本题主要考查算法中的程序框图,渗透阅读、分析与解决问题等素养,认真分析式子结构特征与程序框图结构,即可找出作出选择. 【解析】初始:,因为第一次应该计算=,=2;执行第2次,,因为第二次应该计算=,=3,结束循环,故循环体为,故选A. 【秒杀速解】认真观察计算式子的结构特点,可知循环体为. 2.【2019年高考天津卷】阅读下边的程序框图,运行相应的程序,输出的值为 A.5 B.8 C.24 D.29 【答案】B 【分析】根据程序框图,逐步写出运算结果即可. 【解析】;;,结束循环,输出.故选B. 【名师点睛】解答本题要注意要明确循环体终止的条件是什么,会判断什么时候终止循环体. 3.【2019年高考北京卷】执行如图所示的程序框图,输出的s值为 A.1 B.2 C.3 D.4 【答案】B 【分析】根据程序框图中的条件逐次运算即可. 【解析】初始:,,运行第一次,,,运行第二次,, , 运行第三次,,结束循环,输出,故选B. 【名师点睛】本题考查程序框图,属于容易题,注重基础知识、基本运算能力的考查. 4.【2019年高考全国Ⅰ卷理数】设复数z满足,z在复平面内对应的点为(x,y),则 A. B. C. D. 【答案】C 【分析】本题考点为复数的运算,为基础题目,难度偏易.此题可采用几何法,根据点(x,y)和点(0,1)之间的距离为1,可选正确答案为C. 【解析】由题可得则.故选C. 5.【2019年高考全国Ⅱ卷】设,则 A. B. C. D. 【答案】D 【分析】根据复数的乘法运算法则先求得,然后根据共轭复数的概念写出即可. 【解析】由题可得,所以,故选D. 【名师点睛】本题主要考查复数的乘法运算及共轭复数,是容易题,注重对基础知识、基本计算能力的考查.其中,正确理解概念、准确计算是解答此类问题的关键,部分考生易出现理解性错误. 6.【2019年高考全国Ⅲ卷】若,则 A. B. C. D. 【答案】D 【解析】由题可得.故选D. 【名师点睛】本题考查复数的除法的运算,渗透了数学运算素养.采取运算法则法,利用方程思想解题. 7、【2019年高考全国I卷】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是( ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是.若某人满足上述两个黄金分割比例,且腿长为105 cm,头顶至脖子下端的长度为26 cm,则其身高可能是( ) A.165 cm B.175 cm C.185 cm D.190 cm 【答案】B 【解析】设人体脖子下端至肚脐的长为x cm,肚脐至腿根的长为y cm,则,得.又其腿长为105cm,头顶至脖子下端的长度为26cm,所以其身高约为42.07+5.15+105+26=178.22,接近175cm.故选B. 【名师点睛】本题考查类比归纳与合情推理,渗透了逻辑推理和数学运算素养.采取类比法,利用转化思想解题. 8.【2019年高考全国III卷】记不等式组表示的平面区域为D.命题;命题.下面给出了四个命题 ① ② ③ ④ 这四个命题中,所有真命题的编号是 A.①③ B.①② C.②③ D.③④ 【答案】A 【解析】根据题中的不等式组可作出可行域,如图中阴影部分所示,记直线,由图可知,,所以p为真命题,q为假命题,所以为假命题,为真命题,所以为真命题,为假命题,为真命题,为假命题,所以所有真命题的编号是①③.故选A. 【名师点睛】本题将线性规划和不等式,命题判断综合到一起,解题关键在于充分利用取值验证的方法进行判断. 3.【2019年高考北京卷文数】在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m2−m1=lg,其中星等为mk的星的亮度为Ek(k=1,2).已知太阳的星等是−26.7,天狼星的星等是−1.45,则太阳与天狼星的亮度的比值为 A. 1010.1 B. 10.1 C. lg10.1 D. 10–10.1 【答案】A 【解析】两颗星的星等与亮度满足,令, .故选:A. 一、考向分析: 推理与证明 推理 证明 合情推理 演绎推理 直接证明 间接证明 复数 复数概念 复数运算 算法 三中基本 逻辑结构 条件语句 输入(输出、 赋值)语句) 循环语句 二、考向讲解 考查内容 解 题 技 巧 复数 1.利用复数的四则运算求复数的一般思路: (1)复数的乘法运算满足多项式的乘法法则,利用此法则运算后将实部与虚部分别写出即可. (2)复数的除法运算主要是利用分子、分母同乘分母的共轭复数进行运算化简. (3)利用复数的相关概念解题时,通常是设出复数或利用已知联立方程求解. 2. 判断复数对应的点在复平面内的位置的方法:首先将复数化成a+bi(a,b∈R)的形式,其次根据实部a和虚部b的符号来确定点所在的象限. 3.(1)与共轭复数有关的问题一般都要先设出复数的代数形式,再用待定系数法解决. (2)与复数的概念有关的问题,一般是先化简,把复数的非代数形式化为代数形式. 4.复数的代数运算多用于次数较低的运算,但应用i、ω的性质可简化运算.注意下面结论的灵活运用:(1)(1±i)2=±2i;(2)=i,=-i;(3)ω2+ω+1=0,ω3=1,其中ω=-±i.(4)in+in+1+in+2+in+3=0(n∈N). 算法 1.执行循环结构:首先,要分清是先执行循环体,再判断条件,还是先判断条件,再执行循环体;其次,注意控制循环的变量是什么,何时退出循环;最后,要清楚循环体内的程序是什么,是如何变化的. 2.解答补全问题时,首先,根据输出的结果,计算出需要循环的次数;然后,计算出最后一次循环变量对应的数值;最后,通过比较得出结论.特别要注意对问题的转化,问题与框图的表示的相互转化. 3.解答有关程序框图的问题,要读懂程序框图,熟练掌握程序框图的三种基本结构.注意逐步执行,并且将每一次执行的结果都写出来,要注意在哪一步结束循环以防止运行程序不彻底.循环结构常常用在一些有规律的科学计算中,如累加求和、累乘求积、多次输入等. 4.程序框图中只要有了循环结构,就一定会涉及条件结构和顺序结构.对于循环结构,要注意当型与直到型的区别,搞清进入或终止的循环条件、循环次数是做题的关键. 推理与证明 1.运用归纳推理得出一般结论时,要注意从等式、不等式的项数、次数、系数等多个方面进行综合分析,归纳发现其一般结论. 2.若已给出的式子较少,规律不明显,则可多写出几个式子,从中发现一般结论. 3.进行类比推理时,首先要充分考虑已知对象性质的推理过程,然后类比推导类比对象的性质. 4.归纳推理的关键是找规律,类比推理的关键是看共性. 5.区分两种合情推理的思维过程: (1)归纳推理是由部分到整体、由特殊到一般的推理,归纳推理的思维过程: 实验、观察→概括、推广→猜测一般性结论 (2)类比推理的思维过程:实验、观察→联想、类推→猜测新的结论 在进行类比推理时,不仅要注意形式的类比,还要注意方法的类比.主要有以下两点:(1)找两类对象的对应元素,如:三角形对应三棱锥,圆对应球,面积对应体积等等;(2)找对应元素的对应关系,如:两条边(直线)垂直对应线面垂直或面面垂直,边相等对应面积相等. 考查复数: 例、已知是虚数单位,是的共轭复数,若,则的虚部为 A. B. C. D. 【答案】A 【解析】由题意可得,则,据此可得的虚部为. 例、设为虚数单位,复数满足,则共轭复数的虚部为 A. B. C. D. 【答案】C 【分析】根据条件求出复数,然后再求出共轭复数,从而可得其虚部. 【解析】因为,所以, 所以,所以复数的虚部为.故选C. 【名师点睛】本题考查复数的乘除法的运算及共轭复数的概念,其中正确求出复数是解题的关键,对于复数的运算,解题时一定要按照相关的运算法则求解,特别是在乘除运算中一定不要忘了. 例、知复数满足(其中是虚数单位,满足),则复数的共轭复数是( ) A. B. C. D. 【答案】B 【解析】因为,选B. 例、已知为虚数单位, 为复数的共轭复数,若,则复数在复平面内对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 【答案】A 【解析】设,由,得,即,则,即在复平面内对应的点位于第一象限.故选A. 考查算法: 例、若下图,给出的是计算 值的程序框图,其中判断框内可填入的条件是( ) A. B. C. D. 【答案】C 【解析】程序运行过程中,各变量值如下表所示:第一次循环:i=2,S=0+,第二循环:i=4,S=, 第三次循环:i=6,S=++,…依此类推,第1008次循环:i=2016,S=, i=2018,不满足条件,退出循环,输出s的值,所以i≤2017或i<2017.故答案为:C. 例、已知一个算法的程序框图如图所示,当输出的结果为0时,输入的实数的值为( ) A. -3 B. -3或9 C. 3或-9 D. -9或-3 【答案】B 【解析】结合流程图可知,该流程图等价于计算分段函数: 的函数值, 且函数值为,据此分类讨论:当时, ;当时, ; 综上可得,输入的实数的值为或.本题选择B选项. 例、执行下边的程序框图,如果输入的为0.01,则输出的值等于 A. B. C. D. 【答案】C 【分析】根据程序框图,结合循环关系进行运算,可得结果. 【解析】输入的为,不满足条件;不满足条件;满足条件,结束循环;输出,故选C. 【名师点睛】解答本题关键是利用循环运算,根据计算精确度确定数据分析. 例、在如图所示的计算的程序框图中,判断框内应填入的条件是 A. B. C. D. 【答案】A 【解析】由题意结合流程图可知当时,程序应执行,,再次进入判断框时应该跳出循环,输出的值;结合所给的选项可知判断框内应填入的条件是.故选A. 考查推理与证明 例、如图是网格工作者经常用来解释网络运作的蛇形模型:数字出现在第行;数字出现在第行,数字(从左至右) 出现在第行; 数字出现在第行,依此类推,则第行从左到右第个数字为_________. 【答案】 【解析】前行共有第行最左端的数为第行从左到右第个数字为. 例、观察下列式子:,,,…,根据上述规律,第个不等式应该为 . 【答案】 【解析】由归纳推理易知,答案为。 例、甲、乙、丙、丁四个人参加某项竞赛,四人在成绩公布前做出如下预测: 甲说:获奖者在乙丙丁三人中;乙说:我不会获奖,丙获奖;丙说:甲和丁中的一人获奖; 丁说:乙猜测的是对的. 成绩公布后表明,四人中有两人的预测与结果相符,另外两人的预测与结果不相符.已知俩人获奖,则获奖的是 A.甲和丁 B.甲和丙 C.乙和丙 D.乙和丁 【答案】D 【解析】乙、丁的预测要么同时与结果相符,要么同时与结果不符,若乙、丁的预测成立,则甲、丙的预测不成立,可知矛盾,故乙、丁的预测不成立,从而获奖的是乙和丁,故选D. 【名师点睛】本题考查了逻辑推理能力,假设法是解决此类问题常用的方法. 例、已知是各项均为正数的等差数列,公差为,对任意的是和的等差中项. (Ⅰ)设,求证:是等差数列; (Ⅱ)设 ,求证: 【答案】(Ⅰ)详见解析(Ⅱ)详见解析 【解析】 (I)证明:由题意得,有,因此,所以是等差数列. (II)证明: 所以. 反证法 反证法 假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立,这样的证明方法叫作反证法. 例、用反证法证明命题“设a,b为实数,则方程x3+ax+b=0至少有一个实根”时,要做的假设是( ) A.方程x3+ax+b=0没有实根 B.方程x3+ax+b=0至多有一个实根 C.方程x3+ax+b=0至多有两个实根 D.方程x3+ax+b=0恰好有两个实根 【答案】A 【解析】反证法中否定结论需全否定,“至少有一个”的否定为“一个也没有”. 例、等差数列{an}的前n项和为Sn,a1=1+,S3=9+3. (1)求数列{an}的通项an与前n项和Sn; (2)设bn=(n∈N*),求证:数列{bn}中任意不同的三项都不可能成为等比数列. 【解析】(1)由已知得 所以d=2,故an=2n-1+,Sn=n(n+). (2)证明:由(1),得bn==n+. 假设数列{bn}中存在三项bp,bq,br(p,q,r互不相等)成等比数列, 则b=bpbr,即(q+)2=(p+)(r+),所以(q2-pr)+(2q-p-r)=0. 因为p,q,r∈N*,所以所以2=pr,(p-r)2=0. 所以p=r,这与p≠r矛盾,所以数列{bn}中任意不同的三项都不可能成为等比数列. 反证法证明问题的五个注意点 (1)分清问题的条件和结论; (2)假设所要证的结论不成立,而假设结论的反面成立(否定结论); (3)从假设和条件出发,经过正确的推理,导出与已知条件、公理、定理、定义及明显成立的事实相矛盾或自相矛盾(推导矛盾); (4)因为推理正确,所以断定产生矛盾的原因是“假设”错误,即结论的反面不成立,从而证明了原结论成立(结论成立); (5)应用反证法时,当原命题的结论的反面有多种情况时,要对结论的反面的每一种情况都进行讨论,从而达到否定结论的目的.查看更多