- 2021-04-22 发布 |
- 37.5 KB |
- 54页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习数列大题课件(54张)(全国通用)
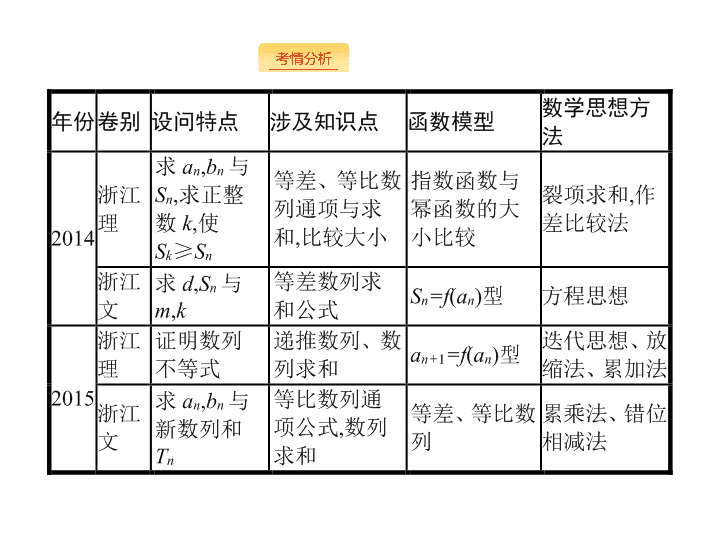
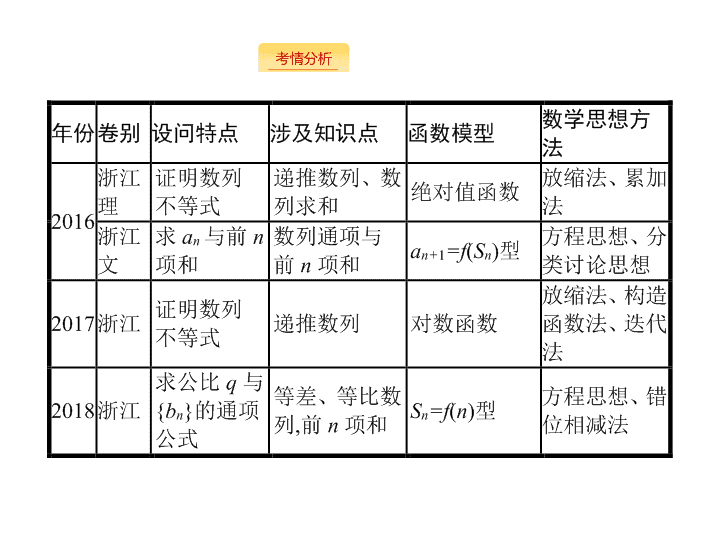
4.3 数列大题 - 2 - - 3 - - 4 - 1 . 求通项公式的常见类型 (1) 已知 a n 与 S n 的关系或 S n 与 n 的关系 , 利用 公式 ( 2) 等差数列、等比数列求通项或转化为等差 ( 比 ) 数列求通项 . (3) 由递推关系式求数列的通项公式 . ① 形如 a n+ 1 =a n +f ( n ), 利用累加法求通项 . ② 形如 a n+ 1 =a n f ( n ), 利用累乘法求通项 . ③ 形如 a n+ 1 =pa n +q , 等式两边同时 加 转化 为等比数列求通项 . - 5 - 2 . 数列求和的常用方法 (1) 公式法 : 利用等差数列、等比数列的求和公式 . (2) 错位相减法 : 适合求数列 { a n · b n } 的前 n 项和 S n , 其中 { a n },{ b n } 一个是等差数列 , 另一个是等比数列 . (3) 裂项相消法 : 即将数列的通项分成两个式子的代数和 , 通过累加抵消中间若干项的方法 . (4) 拆项分组法 : 先把数列的每一项拆成两项 ( 或多项 ), 再重新组合成两个 ( 或多个 ) 简单的数列 , 最后分别求和 . (5) 并项求和法 : 把数列的两项 ( 或多项 ) 组合在一起 , 重新构成一个数列再求和 , 适用于正负相间排列的数列求和 . - 6 - 3 . 数列单调性的常见题型及方法 (1) 求最大 ( 小 ) 项时 , 可利用 : ① 数列的单调性 ; ② 函数的单调性 ; ③ 导数 . (2) 求参数范围时 , 可利用 : ① 作差法 ; ② 同号递推法 ; ③ 先猜后证法 . 4 . 数列不等式问题的解决方法 (1) 利用数列 ( 或函数 ) 的单调性 . (2) 放缩法 : ① 先求和后放缩 ; ② 先放缩后求和 , 包括放缩后成等差 ( 或等比 ) 数列再求和 , 或者放缩后裂项相消再求和 . - 7 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 4 . 3 . 1 等差、等比数列的通项及求和 等差、等比数列的通项及求和 例 1 (2013 浙江 , 理 18) 在公差为 d 的等差数列 { a n } 中 , 已知 a 1 = 10, 且 a 1 ,2 a 2 + 2,5 a 3 成等比数列 . (1) 求 d , a n ; (2) 若 d< 0, 求 |a 1 |+|a 2 |+|a 3 |+ … +|a n |. - 8 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 解 : (1) 由题意得 5 a 3 ·a 1 = (2 a 2 + 2) 2 , 即 d 2 - 3 d- 4 = 0, 故 d=- 1 或 d= 4 . 所以 a n =-n+ 11, n ∈ N * 或 a n = 4 n+ 6, n ∈ N * . (2) 设数列 { a n } 的前 n 项和为 S n . 因为 d< 0, 由 (1) 得 d=- 1, a n =-n+ 11 . - 9 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 解题心得 对于等差、等比数列 , 求其通项及前 n 项和时 , 只需利用等差数列或等比数列的通项公式及求和公式求解即可 . - 10 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 对点训练 1 已知等差数列 { a n } 的公差不为零 , a 1 = 25, 且 a 1 , a 11 , a 13 成等比数列 . (1) 求 { a n } 的通项公式 ; (2) 求 a 1 +a 4 +a 7 + … +a 3 n- 2 . 解 : (1) 设 { a n } 的公差为 d. 由题意 , 得 = a 1 a 13 , 即 ( a 1 + 10 d ) 2 =a 1 ( a 1 + 12 d ) . 于是 d (2 a 1 + 25 d ) = 0 . 又 a 1 = 25, 所以 d= 0( 舍去 ) 或 d=- 2 . 故 a n =- 2 n+ 27 . (2) 令 S n =a 1 +a 4 +a 7 + … +a 3 n- 2 . 由 (1) 知 a 3 n- 2 =- 6 n+ 31, 故 { a 3 n- 2 } 是首项为 25, 公差为 - 6 的等差数列 . - 11 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 - 12 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 - 13 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 - 14 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 解题心得 无论是求数列的通项还是求数列的前 n 项和 , 解题基本思路是通过变形、整理后 , 能够把所给数列转化为等差数列或等比数列 , 然后利用等差数列或等比数列的通项公式或求和公式解决问题 . - 15 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 对点训练 2 设 { a n } 是公比大于 1 的等比数列 , S n 为数列 { a n } 的前 n 项和 , 已知 S 3 = 7, 且 a 1 + 3,3 a 2 , a 3 + 4 构成等差数列 . (1) 求数列 { a n } 的通项 ; (2) 令 b n = ln a 3 n+ 1 , n= 1,2, … , 求数列 { b n } 的前 n 项和 T n . - 16 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 - 17 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考向三 数列的前 n 项和与等差、等比通项 例 3 (2009 浙江 , 文 20) 设 S n 为数列 { a n } 的前 n 项和 , S n =kn 2 +n , n ∈ N * , 其中 k 是常数 . (1) 求 a 1 及 a n ; (2) 若对于任意的 m ∈ N * , a m , a 2 m , a 4 m 成等比数列 , 求 k 的值 . - 18 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考向三 解 : (1) 由 S n =kn 2 +n , 得 a 1 =S 1 =k+ 1, a n =S n -S n- 1 = 2 kn-k+ 1( n ≥ 2) . a 1 =k+ 1 也满足上式 , 所以 a n = 2 kn-k+ 1, n ∈ N * . (2) 由 a m 、 a 2 m 、 a 4 m 成等比数列 , 得 (4 mk-k+ 1) 2 = (2 km-k+ 1)(8 km-k+ 1), 将上式化简 , 得 2 km ( k- 1) = 0, 因为 m ∈ N * , 所以 m ≠0, 故 k= 0, 或 k= 1 . - 19 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考向三 解题心得 已知数列 { a n } 的前 n 项和 S n 表达式求 a n , 则一般要用 公式 来 处理 , 然后再应用等差、等比数列的公式来解决问题 . - 20 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考向三 对点训练 3 (2014 浙江 , 文 19) 已知等差数列 { a n } 的公差 d> 0 . 设 { a n } 的前 n 项和为 S n , a 1 = 1, S 2 · S 3 = 36 . (1) 求 d 及 S n ; (2) 求 m , k ( m , k ∈ N * ) 的值 , 使得 a m +a m+ 1 +a m+ 2 + … +a m+k = 65 . 解析 : (1) 由题意知 (2 a 1 +d )(3 a 1 + 3 d ) = 36, 将 a 1 = 1 代入上式解得 d= 2 或 d=- 5 . 因为 d> 0, 所以 d= 2 . 从而 a n = 2 n- 1, S n =n 2 ( n ∈ N * ) . (2) 由 (1) 得 a m +a m+ 1 +a m+ 2 + … +a m+k = (2 m+k- 1)( k+ 1) . 所以 (2 m+k- 1)( k+ 1) = 65 . 由 m , k ∈ N * 知 2 m+k- 1 >k+ 1 > 1 , - 21 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 4 . 3 . 2 数列的通项及求和 求数列的通项及错位相减求和 例 1 (2018 浙江 , 理 20) 已知等比数列 { a n } 的公比 q> 1, 且 a 3 +a 4 +a 5 = 28, a 4 + 2 是 a 3 , a 5 的等差中项 . 数列 { b n } 满足 b 1 = 1, 数列 {( b n+ 1 -b n ) a n } 的前 n 项和为 2 n 2 +n. (1) 求 q 的值 ; (2) 求数列 { b n } 的通项公式 . - 22 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 - 23 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 - 24 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 - 25 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 解题心得 求数列通项的基本方法是利用等差、等比数列通项公式 , 或通过变形转换成等差、等比数列求通项 ; 如果数列 { a n } 与数列 { b n } 分别是等差数列和等比数列 , 那么数列 { a n ·b n } 的前 n 项和采用错位相减法来求 . - 26 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 对点训练 1 (2012 浙江 , 文 19) 已知数列 { a n } 的前 n 项和为 S n , 且 S n = 2 n 2 +n , n ∈ N * , 数列 { b n } 满足 a n = 4log 2 b n + 3, n ∈ N * . (1) 求 a n , b n ;( 2) 求数列 { a n · b n } 的前 n 项和 T n . 解 : (1) 由 S n = 2 n 2 +n , 得当 n= 1 时 , a 1 =S 1 = 3; 当 n ≥ 2 时 , a n =S n -S n- 1 = 4 n- 1 . 所以 a n = 4 n- 1, n ∈ N * . 由 4 n- 1 =a n = 4log 2 b n + 3, 得 b n = 2 n- 1 , n ∈ N * . (2) 由 (1) 知 a n b n = (4 n- 1) · 2 n- 1 , n ∈ N * . 所以 T n = 3 + 7 × 2 + 11 × 2 2 + … + (4 n- 1) · 2 n- 1 ,2 T n = 3 × 2 + 7 × 2 2 + … + (4 n- 5) · 2 n- 1 + (4 n- 1) · 2 n , 所以 2 T n -T n = (4 n- 1)2 n - [3 + 4(2 + 2 2 + … + 2 n- 1 )] = (4 n- 5)2 n + 5 . 故 T n = (4 n- 5)2 n + 5, n ∈ N * . - 27 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 - 28 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 - 29 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 解题心得 先用等差、等比数列的通项与求和公式算出 a n , S n , 然后 发现 可 拆成两项之差 , 求和时中间的项能够抵消 , 从而求得和 , 注意抵消后所剩余的项一般前后对称 . 另在比较大小时要进行简单的放缩 . - 30 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 对点训练 2 (2018 天津 , 理 18) 设 { a n } 是等比数列 , 公比大于 0, 其前 n 项和为 S n ( n ∈ N * ),{ b n } 是等差数列 . 已知 a 1 = 1, a 3 =a 2 + 2, a 4 =b 3 +b 5 , a 5 =b 4 + 2 b 6 . (1) 求 { a n } 和 { b n } 的通项公式 ; (2) 设数列 { S n } 的前 n 项和为 T n ( n ∈ N * ), ① 求 T n ; - 31 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 (1) 解 : 设等比数列 { a n } 的公比为 q. 由 a 1 = 1, a 3 =a 2 + 2, 可得 q 2 -q- 2 = 0 . 因为 q> 0, 可得 q= 2, 故 a n = 2 n- 1 . 设等差数列 { b n } 的公差为 d. 由 a 4 =b 3 +b 5 , 可得 b 1 + 3 d= 4 . 由 a 5 =b 4 + 2 b 6 , 可得 3 b 1 + 13 d= 16, 从而 b 1 = 1, d= 1, 故 b n =n. 所以 , 数列 { a n } 的通项公式为 a n = 2 n- 1 , 数列 { b n } 的通项公式为 b n =n . - 32 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考向三 涉及奇偶数讨论的数列求和 例 3 已知等差数列 { a n } 的前 n 项和为 S n , 且 a 1 = 2, S 5 = 30 . 数列 { b n } 的前 n 项和为 T n , 且 T n = 2 n - 1 . (1) 求数列 { a n },{ b n } 的通项公式 ; (2) 设 c n = ( - 1) n ( a n b n + ln S n ), 求数列 { c n } 的前 n 项和 . ∴ d= 2, ∴ a n = 2 n. 对数列 { b n }: 当 n= 1 时 , b 1 =T 1 = 2 1 - 1 = 1, 当 n ≥ 2 时 , b n =T n -T n- 1 = 2 n - 2 n- 1 = 2 n- 1 , 当 n= 1 时也满足上式 . ∴ b n = 2 n- 1 . - 33 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考向三 (2) c n = ( - 1) n ( a n b n + ln S n ) = ( - 1) n a n b n + ( - 1) n ln S n . ∴ ln S n = ln n ( n+ 1) = ln n+ ln( n+ 1) . 而 ( - 1) n a n b n = ( - 1) n · 2 n· 2 n- 1 =n· ( - 2) n , 设数列 {( - 1) n a n b n } 的前 n 项和为 A n , 数列 {( - 1) n ln S n } 的前 n 项和为 B n , 则 A n = 1 × ( - 2) 1 + 2 × ( - 2) 2 + 3 × ( - 2) 3 + … +n· ( - 2) n , ① 则 - 2 A n = 1 × ( - 2) 2 + 2 × ( - 2) 3 + 3 × ( - 2) 4 + … +n· ( - 2) n+ 1 , ② - 34 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考向三 当 n 为偶数时 , B n =- (ln 1 + ln 2) + (ln 2 + ln 3) - (ln 3 + ln 4) + … + [ln n+ ln( n+ 1)] = ln( n+ 1) - ln 1 = ln( n+ 1); 当 n 为奇数时 , B n =- (ln 1 + ln 2) + (ln 2 + ln 3) - (ln 3 + ln 4) + … - [ln n+ ln( n+ 1)] =- ln( n+ 1) - ln 1 =- ln( n+ 1) . 由以上可知 , B n = ( - 1) n ln( n+ 1 ) . - 35 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考向三 对点训练 3 已知函数 f ( x ) = 4 x ,4, f ( a 1 ), f ( a 2 ), … , f ( a n ),2 n+ 3 ( n ∈ N * ) 成等比数列 . (1) 求数列 { a n } 的通项公式 ; - 36 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考向三 - 37 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考向三 - 38 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 4 . 3 . 3 数列中的证明及存在性问题 等差 ( 比 ) 数列的证明与判断 ( 1) 求 a 1 , a 2 ; (2) 求数列 { a n } 的通项公式 , 并证明数列 { a n } 是等差数列 ; (3) 如果数列 { b n } 满足 a n = log 2 b n , 试证明数列 { b n } 是等比数列 , 并求其前 n 项和 T n . - 39 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 - 40 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 解题心得 1 . 判断和证明数列是等差 ( 比 ) 数列的三种方法 . ( 2) 通项公式法 : 若 a n =kn+b ( n ∈ N * ), 则 { a n } 为等差数列 ; 若 a n =pq kn+b ( n ∈ N * ), 则 { a n } 为等比数列 . (3) 中项公式法 : 若 2 a n =a n- 1 +a n+ 1 ( n ∈ N * , n ≥ 2), 则 { a n } 为等差数列 ; 若 = a n- 1 ·a n+ 1 ( n ∈ N * , n ≥ 2), 则 { a n } 为等比数列 . 2 . 对已知数列 a n 与 S n 的关系 , 证明 { a n } 为等差或等比数列的问题 , 解题思路是 : 由 a n 与 S n 的关系递推出 n+ 1 时的关系式 , 两个关系式相减后 , 进行化简、整理 , 最终化归为用定义法证明 . - 41 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 对点训练 1 设数列 { a n } 的前 n 项和为 S n , 且首项 a 1 ≠3, a n+ 1 =S n + 3 n ( n ∈ N * ) . (1) 求证 :{ S n - 3 n } 是等比数列 ; (2) 若 { a n } 为递增数列 , 求 a 1 的取值范围 . - 42 - 4.3.1 4.3.2 4.3.3 考向一 考 向二 考 向三 (1) 证明 ∵ a n+ 1 =S n + 3 n , ∴ S n+ 1 = 2 S n + 3 n . ∴ S n+ 1 - 3 n+ 1 = 2( S n - 3 n ) . ∵ a 1 ≠3, ∴ 数列 { S n - 3 n } 是首项为 a 1 - 3, 公比为 2 的等比数列 . (2) 解 : 由 (1) 得 , S n - 3 n = ( a 1 - 3) × 2 n- 1 . ∴ S n = ( a 1 - 3) × 2 n- 1 + 3 n . 当 n ≥ 2 时 , a n =S n -S n- 1 = ( a 1 - 3) × 2 n- 2 + 2 × 3 n- 1 . ∵ { a n } 为递增数列 , ∴ 当 n ≥ 2 时 ,( a 1 - 3) × 2 n- 1 + 2 × 3 n > ( a 1 - 3) × 2 n- 2 + 2 × 3 n- 1 , ∵ a 2 =a 1 + 3 >a 1 , ∴ a 1 的取值范围是 ( - 9, +∞ ) . - 43 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 - 44 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 - 45 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 解题心得 要证明数列不等式 , 首先要进行变形放缩 , 然后通过迭代、累加等方法得出结论 , 而且一般情况下 , 第 (1) 问的结论可为第 (2) 问应用 . - 46 - 4.3.1 4.3.2 4.3.3 考向一 考向二 考 向三 对点训练 2 (2017 浙江 , 文 22) 已知数列 { x n } 满足 : x 1 = 1, x n =x n+ 1 + ln(1 +x n+ 1 )( n ∈ N * ) . 证明 : 当 n ∈ N * 时 , (1)0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档