- 2021-04-22 发布 |
- 37.5 KB |
- 5页


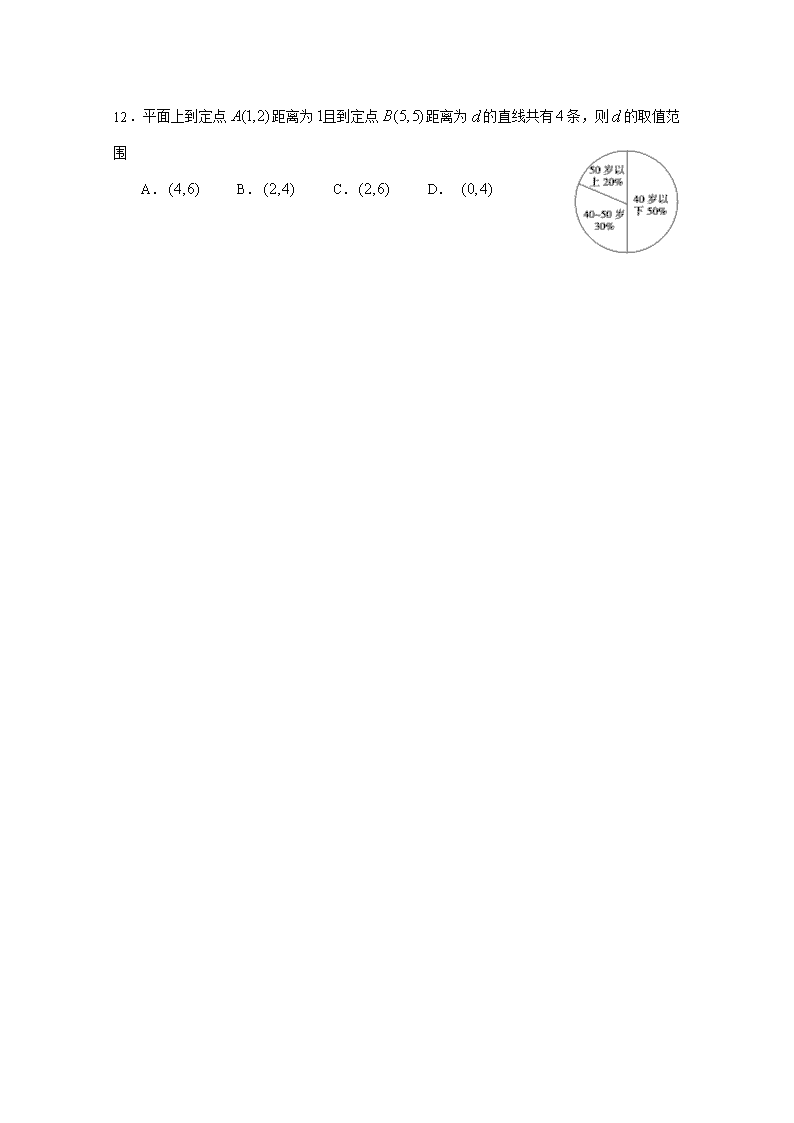
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年湖北省沙市中学高二上学期第四次半月考数学(理)试题 缺答案
2017-2018学年湖北省沙市中学高二上学期第四次半月考理数试卷 考试时间:2017年11月2日 一、选择题(本题共12个小题,每题只有一个正确答案 ,每题5分,共60分。请把答案涂在答题卡上) 1.把化为十进制数为( ) A.60 B.68 C.70 D.74 2.下面程序执行后输出的结果是( ) A.4 B. C. D. 3.如图所示程序,若输入的两位数是83,则输出的结果为( ) A.83 B.38 C.3 D.8 4.两圆与的公共弦长等于( ) A.4 B.2 C.3 D.4 5. 如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,其中茎为十位数,叶为个位数,甲、乙两人得分的中位数为X甲、X乙,则下列判断正确的是 A. X乙 - X甲 = 5,甲比乙得分稳定 B. X乙 - X甲 = 5,乙比甲得分稳定 C. X乙 - X甲 = 10,甲比乙得分稳定 D. X乙 - X甲 = 10,乙比甲得分稳定 6.已知点在直线上移动,当 取得最小值时,过点引圆的切线,则此切线段的长度为 ( ) A. B. C. D. 7.某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270,使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段,如果抽得号码有下列四种情况: ①7,34,61,88,115,142,169,196,223,250 ②5,9,100,107,111,121,180,195,200,265 ③11,38,65,92,119,146,173,200,227,254 ④30,57,84,111,138,165,192,219,246,270 关于上述样本的下列结论中,正确的是( ) A.②、③都不能为系统抽样 B.②、④都不能为分层抽样 C.①、④都可能为系统抽样 D.①、③都可能为分层抽样 8.若点和在直线的两侧,则直线倾斜角的取值范围是( ) A. B. C. D. 9.已知为坐标原点,,点的坐标满足约束条件,则 最大值为( ) A.-2 B.-1 C.1 D.2 10.在平面直角坐标系中,分别是轴和轴上的动点,若以为直径的圆与直线相切,则圆面积的最小值为( ) A. B. C. D. 11.为求使不等式成立的最大正整数,设计了 如图所示的算法,则图中“ ”处应填入 A. B. C. D. 12.平面上到定点距离为且到定点距离为的直线共有条,则的取值范围 A. B. C. D. 二、填空题(本题共4个小题,每题5分,共计20分.请把答案写在答题纸上) 13.200名职工年龄分布如图所示,从中随机抽取40名职工作样本,采用系统抽样方法,按1~200编号分为40组,分别为1~5,6~10,…,196~200,第5组抽取号码为22,第8组抽取号码为________.若采用分层抽样,40岁以下年龄段应抽取________人. 14.已知圆在曲线的内部,则半径的范围是_____________. 15.圆的方程为,圆的方程为 .过圆上任意一点作圆的两条切线,切点分别为,则的最小值是________. 16.已知平面上的线段及点,任取上一点,线段长度的最小值称为到的距离,记作 (1)求点到线段的距离=_______; (2)设是长为2的线段,求点的集合所表示的图形面积_______. 三、解答题(本题共6个小题 共计70分。请把解答过程写在答题纸上) 17.已知直线, (1)若直线过点(3,2)且,求直线的方程; (2)若直线过与直线的交点,且,求直线的方程. 18.已知关于的方程. (1)当为何值时,方程表示圆. (2)若圆与直线相交于两点,且,求的值. 19.如图,在四棱锥中,底面,,, ,,是的中点. (1)求证:; (2)求二面角的余弦值。 20.某校2017-2018学年高二某个班的一次化学考试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图: (1)求分数在[50,60)的频率及在全班人数; (2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高; (3)利用频率分布直方图估计这个班此次化学成绩的中位数(结果保留两位小数). 21、已知以点为圆心的圆与轴交于点,与轴交于点,其中为原点. (1)求证:的面积为定值; (2)设直线与圆交于点,若,求圆C的方程; (3)是(2)中所求圆内相互垂直的两条弦,垂足为,求四边形面积的最大值. 22.己知圆和直线,在轴上有一点,在圆上有不与重合的两动点,设直线斜率为,直线斜率为,直线斜率为, (l)若 ①求出点坐标; ②交于,交于,求证:以为直径的圆,总过定点,并求出定点坐标. (2)若,判断直线是否经过定点,若有,求出来,若没有,请说明理由.查看更多