山西省长治市2020届高三（3月在线）综合测试 数学（文）

山西省长治市2020届高三（3月在线）综合测试 数学（文）

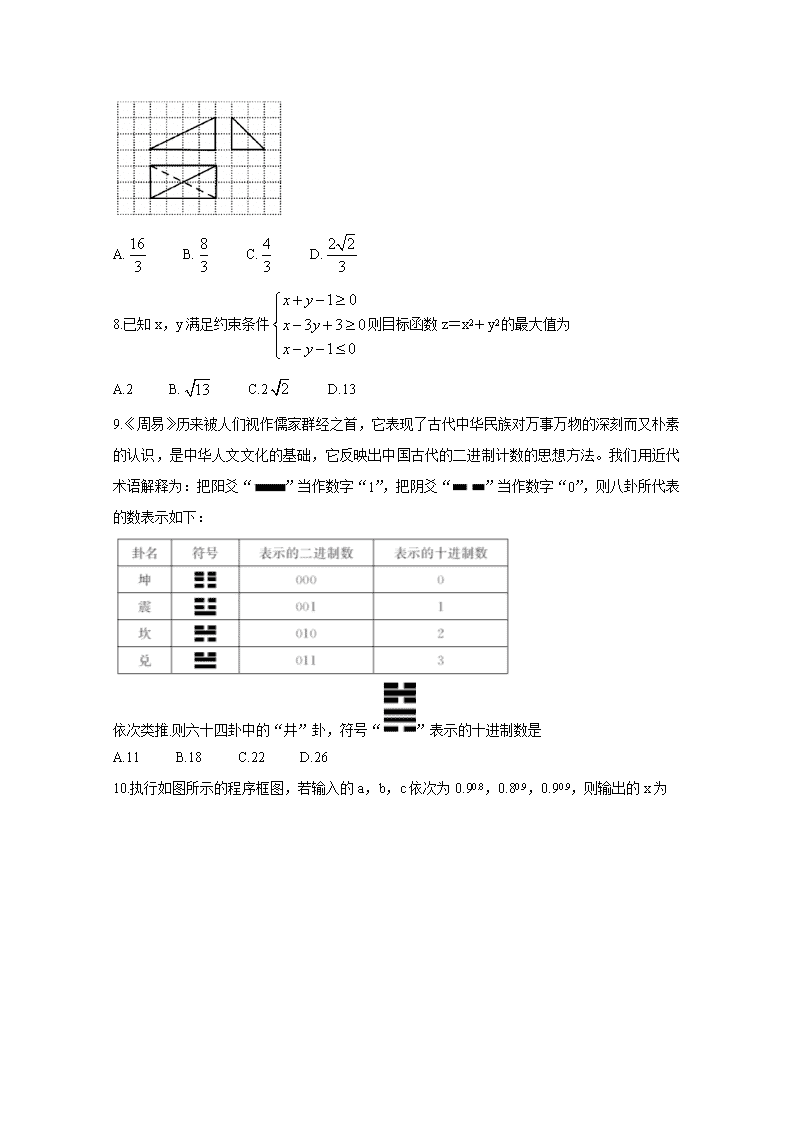
文科数学试题 注意事项：‎ ‎1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。‎ ‎2.考试时间为120分钟，满分150分。‎ ‎3.答题前，考生务必将自己的姓名、准考证号填写在答题卡相应的位置。‎ ‎4.全部答案在答题卡上完成，答在本试卷上无效。‎ 第I卷(选择题 共60分)‎ 一、选择题：本题共12小题，每题5分，共计60分，在每小题给出的四个选项中，只有一个选项正确。‎ ‎1.已知集合A＝{x|log3x<1}，B＝{x|x≥1}，则A∩B＝‎ A.{1，2} B.{1，2，3} C.[1，3) D.(3，＋∞)‎ ‎2.已知i为虚数单位，z＝，则复数的虚部为 A.－2i B.2i C.2 D.－2‎ ‎3.函数y＝tan(2x＋)的图象 A.关于原点对称 B.关于点(－，1)对称 C.关于直线x＝－对称 D.关于点(，0)对称 ‎4.根据党中央关于“精准”脱贫的要求，某市农业经济部门派三位专家对A、B、C三个县区进行调研，每个县区派一位专家，则甲专家恰好派遣至A县区的概率为 A. B. C. D.‎ ‎5.已知向量，满足||＝1，||＝2，|＋|＝，则在上的投影为 A.1 B. C.2 D.‎ ‎6.已知椭圆与双曲线的焦点相同，则椭圆的离心率为 A. B. C. D.‎ ‎7.如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该几何体的体积为 A. B. C. D.‎ ‎8.已知x，y满足约束条件则目标函数z＝x2＋y2的最大值为 A.2 B. C.2 D.13‎ ‎9.《周易》历来被人们视作儒家群经之首，它表现了古代中华民族对万事万物的深刻而又朴素的认识，是中华人文文化的基础，它反映出中国古代的二进制计数的思想方法。我们用近代术语解释为：把阳爻“”当作数字“1”，把阴爻“”当作数字“0”，则八卦所代表的数表示如下：‎ 依次类推.则六十四卦中的“井”卦，符号“”表示的十进制数是 A.11 B.18 C.22 D.26‎ ‎10.执行如图所示的程序框图，若输入的a，b，c依次为0.90.8，0.80.9，0.90.9，则输出的x为 A.0.90.8 B.0.80.9 C.0.90.9 D.0.80.8‎ ‎(‎ ‎11.已知函数f(x)＝，若函数g(x)＝f(x)－ax恰有2个零点，则a的取值范围是 A.(1，＋∞) B.[1.2] C.[1，2) D.(0，2)‎ ‎12.已知动点M到点F(1，0)的距离与到y轴距离之和为3，动点N在直线2x－y＋4＝0上，则两点距离|MN|的最小值是 A. B. C. D.‎ 第II卷(非选择题，共90分)‎ 二、填空题：本题共4小题，每题5分，共计20分。请把正确答案填写在答题纸相应的位置上。‎ ‎13.cos75°－cos15°的值是 。‎ ‎14.已知定义在R上的函数f(x)满足f(1＋x)＝－f(3－x)，且f(x)的图像与g(x)＝lg的图像有四个交点，则这四个交点的横纵坐标之和等于 。‎ ‎15.已知球的直径SC＝2。A，B是该球球面上的两点，AB＝，∠ASC＝∠BSC＝45°，则棱锥S－ABC的体积为 。‎ ‎16.在△ABC中，角A、B、C所对的边分别为a、b、c，已知c＝4，(2a＋b)cosC＋ccosB＝0。则△ABC面积的最大值是 。‎ 三、解答题：本题共6小题，共计70分。‎ ‎17.(本小题满分12分)‎ 在公差大于1的等差数列{an}中，a4＝13。且a3，a6＋1。a13成等比数列。‎ ‎(1)求数列{an}的通项公式；‎ ‎(2)令bn＝，求数列{bn}的前n项和Sn。‎ ‎18.(本小题满分12分)‎ 如图，在四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，且PA＝AD＝2，AB＝3，点E为线段PD的中点。‎ ‎(1)求证：AE⊥PC；‎ ‎(2)求三棱锥P－ACE的体积。‎ ‎19.(本小题满分12分)‎ 为了丰富学生的课外文化生活，某中学积极探索开展课外文体活动的新途径及新形式，取得了良好的效果。为了调查学生的学习积极性与参加文体活动是否有关，学校对200名学生做了问卷调查，列联表如下：‎ 已知在全部200人中随机抽取1人，抽到学习积极性不高的学生的概率为。‎ ‎(1)请将上面的列联表补充完整；‎ ‎(2)是否有99.9%的把握认为学习积极性高与参加文体活动有关?请说明你的理由；‎ ‎(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人，‎ 再从所选出的5人中随机选取2人，求至少有1人学习积极性不高的概率。‎ 附：‎ ‎，其中n＝a＋b＋c＋d。‎ ‎20.(本小题满分12分)‎ 已知椭圆C：，点A(2，0)、P(x0，y0)。Q(－x0，－y0)(y0≠0)在椭圆上，直线AP与直线AQ的斜率之积kAP·kAQ＝－。‎ ‎(1)求椭圆的标准方程；‎ ‎(2)已知直线l：点E(－1，0)关于直线l的对称点是D，求证：过点P，D的直线恒过定点。‎ ‎21.(本小题满分12分)‎ 已知函数f(x)＝ex－ax－1。‎ ‎(1)讨论函数f(x)的单调性；‎ ‎(2)当x>0时，f(x)≥x2－x恒成立，求实数a的取值范围。‎ 请考生在第22、23二题中任选一题作答，如果多做，则按所做的第一题记分。解答时请写清题号。‎ ‎22.选修4－4：坐标系与参数方程(本小题满分10分)。‎ 在直角坐标系xOy中，曲线C1的方程为(t为参数)。以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝2sinθ。‎ ‎(1)求C1，C2的普通方程；‎ ‎(2)设点A在曲线C1上，且对应的t＝2，点B是曲线C2上的点，求AOB面积的最大值。‎ ‎23.选修4－5：不等式选讲(本小题满分10分)‎ 已知函数，f(x)＝|2x－1|＋|x－a|。‎ ‎(1)当a＝1时，求不等式f(x)>2的解集；‎ ‎(2)若不等式f(x)<2x在x∈[1，2]上恒成立，求实数a的取值范围。‎