- 2021-04-22 发布 |
- 37.5 KB |
- 10页
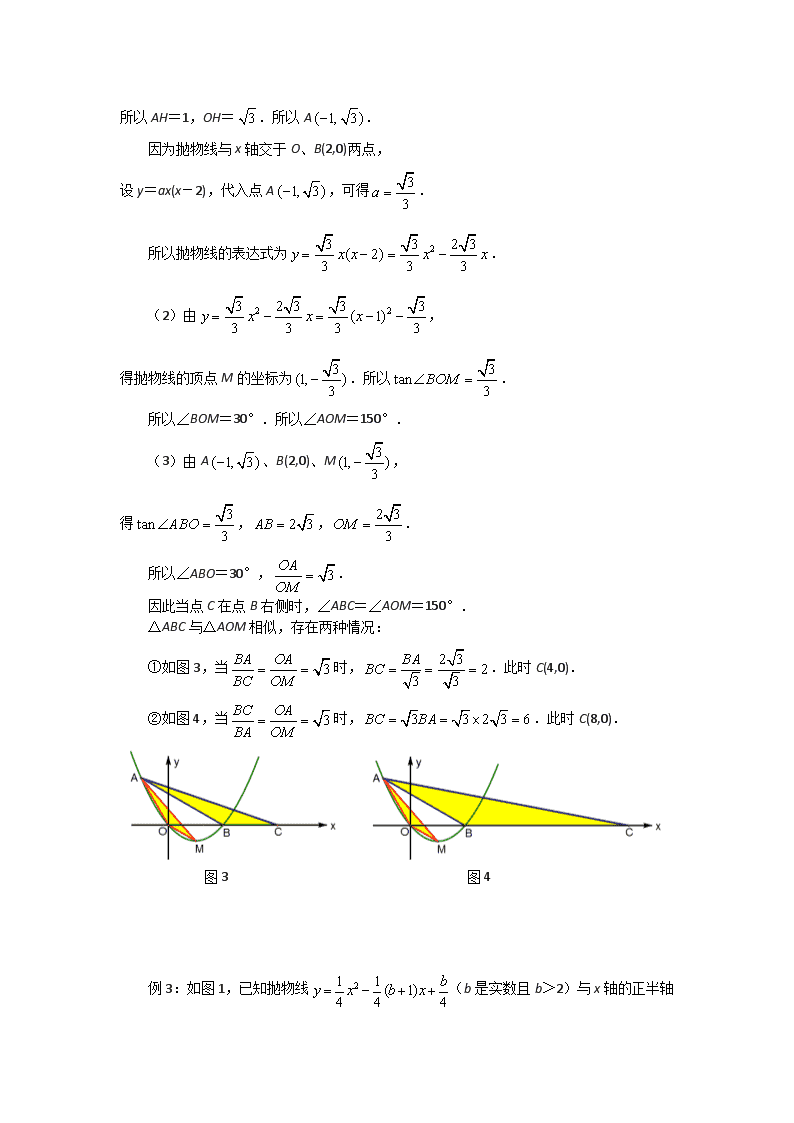
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考压轴题之相似含非常详细的解答
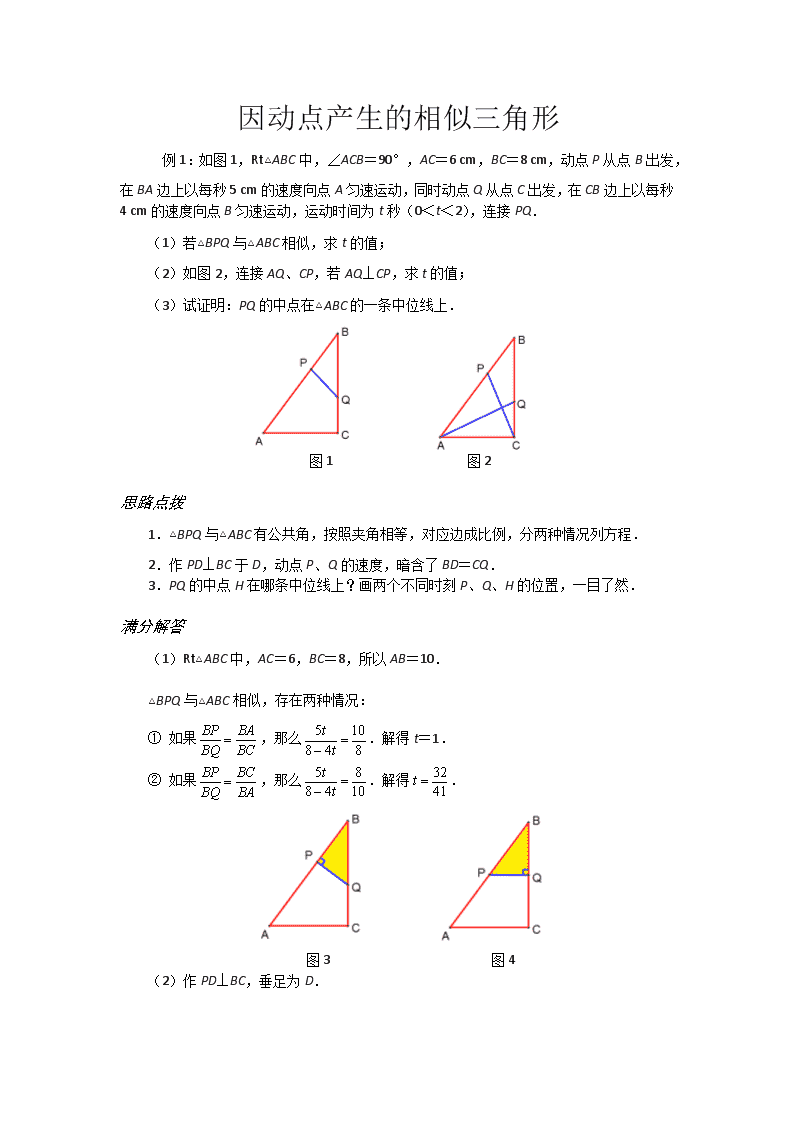
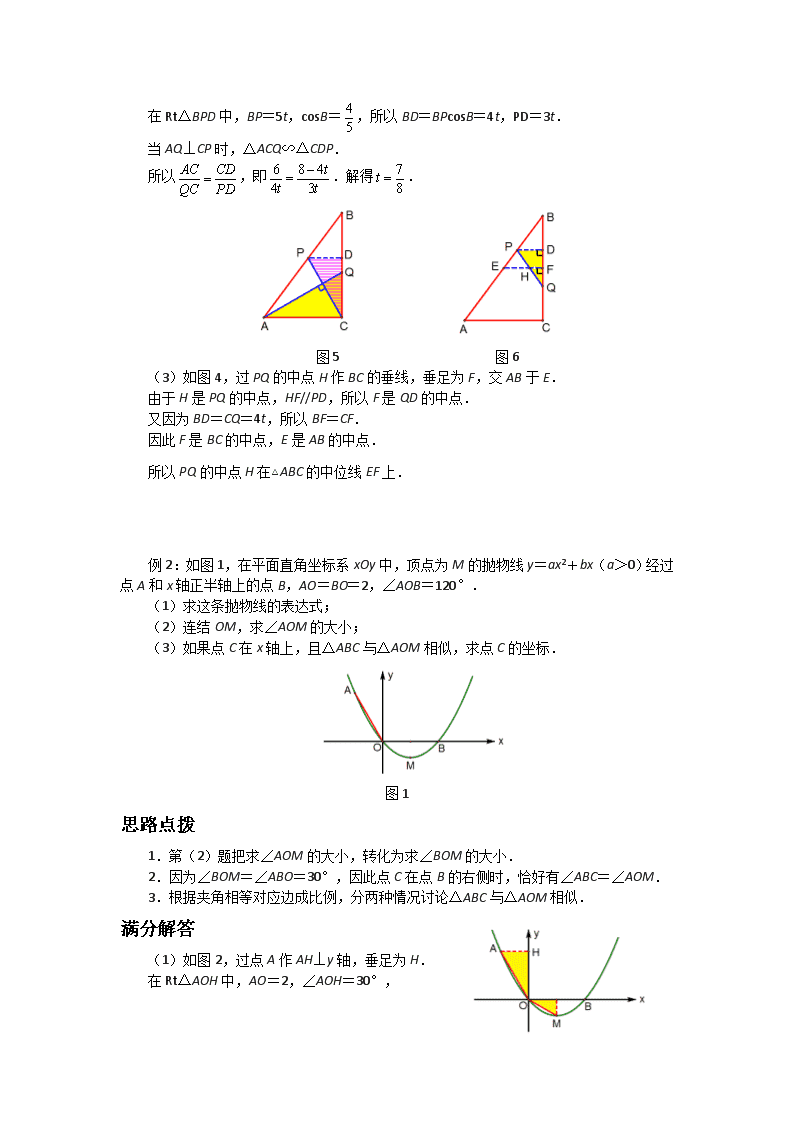
因动点产生的相似三角形 例1:如图1,Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ. (1)若△BPQ与△ABC相似,求t的值; (2)如图2,连接AQ、CP,若AQ⊥CP,求t的值; (3)试证明:PQ的中点在△ABC的一条中位线上. 图1 图2 思路点拨 1.△BPQ与△ABC有公共角,按照夹角相等,对应边成比例,分两种情况列方程. 2.作PD⊥BC于D,动点P、Q的速度,暗含了BD=CQ. 3.PQ的中点H在哪条中位线上?画两个不同时刻P、Q、H的位置,一目了然. 满分解答 (1)Rt△ABC中,AC=6,BC=8,所以AB=10. △BPQ与△ABC相似,存在两种情况: ① 如果,那么.解得t=1. ② 如果,那么.解得. 图3 图4 (2)作PD⊥BC,垂足为D. 在Rt△BPD中,BP=5t,cosB=,所以BD=BPcosB=4t,PD=3t. 当AQ⊥CP时,△ACQ∽△CDP. 所以,即.解得. 图5 图6 (3)如图4,过PQ的中点H作BC的垂线,垂足为F,交AB于E. 由于H是PQ的中点,HF//PD,所以F是QD的中点. 又因为BD=CQ=4t,所以BF=CF. 因此F是BC的中点,E是AB的中点. 所以PQ的中点H在△ABC的中位线EF上. 例2:如图1,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°. (1)求这条抛物线的表达式; (2)连结OM,求∠AOM的大小; (3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标. 图1 思路点拨 1.第(2)题把求∠AOM的大小,转化为求∠BOM的大小. 2.因为∠BOM=∠ABO=30°,因此点C在点B的右侧时,恰好有∠ABC=∠AOM. 3.根据夹角相等对应边成比例,分两种情况讨论△ABC与△AOM相似. 满分解答 (1)如图2,过点A作AH⊥y轴,垂足为H. 在Rt△AOH中,AO=2,∠AOH=30°, 所以AH=1,OH=.所以A. 因为抛物线与x轴交于O、B(2,0)两点, 设y=ax(x-2),代入点A,可得. 所以抛物线的表达式为. (2)由, 得抛物线的顶点M的坐标为.所以. 所以∠BOM=30°.所以∠AOM=150°. (3)由A、B(2,0)、M, 得,,. 所以∠ABO=30°,. 因此当点C在点B右侧时,∠ABC=∠AOM=150°. △ABC与△AOM相似,存在两种情况: ①如图3,当时,.此时C(4,0). ②如图4,当时,.此时C(8,0). 图3 图4 例3:如图1,已知抛物线(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B是左侧),与y轴的正半轴交于点C. (1)点B的坐标为______,点C的坐标为__________(用含b的代数式表示); (2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由; (3)请你进一步探索在第一象限内是否存在点Q,使得△QCO、△QOA和△QAB 中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由. 图1 思路点拨 1.第(2)题中,等腰直角三角形PBC暗示了点P到两坐标轴的距离相等. 2.联结OP,把四边形PCOB重新分割为两个等高的三角形,底边可以用含b的式子表示. 3.第(3)题要探究三个三角形两两相似,第一直觉这三个三角形是直角三角形,点Q最大的可能在经过点A与x轴垂直的直线上. 满分解答 (1)B的坐标为(b, 0),点C的坐标为(0, ). (2)如图2,过点P作PD⊥x轴,PE⊥y轴,垂足分别为D、E,那么△PDB≌△PEC. 因此PD=PE.设点P的坐标为(x, x). 如图3,联结OP. 所以S四边形PCOB=S△PCO+S△PBO==2b. 解得.所以点P的坐标为(). 图2 图3 (3)由,得A(1, 0),OA=1. ①如图4,以OA、OC为邻边构造矩形OAQC,那么△OQC≌△QOA. 当,即时,△BQA∽△QOA. 所以.解得.所以符合题意的点Q为(). ②如图5,以OC为直径的圆与直线x=1交于点Q,那么∠OQC=90°。 因此△OCQ∽△QOA. 当时,△BQA∽△QOA.此时∠OQB=90°. 所以C、Q、B三点共线.因此,即.解得.此时Q(1,4). 图4 图5 例4:程C1: (m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧. (1)若抛物线C1过点M(2, 2),求实数m的值; (2)在(1)的条件下,求△BCE的面积; (3)在(1)的条件下,在抛物线的对称轴上找一点H,使得BH+EH最小,求出点H的坐标; (4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由. 图1 思路点拨 1.第(3)题是典型的“牛喝水”问题,当H落在线段EC上时,BH+EH最小. 2.第(4)题的解题策略是:先分两种情况画直线BF,作∠CBF=∠EBC=45°,或者作BF//EC.再用含m的式子表示点F的坐标.然后根据夹角相等,两边对应成比例列关于m的方程. 满分解答 (1)将M(2, 2)代入,得.解得m=4. (2)当m=4时,.所以C(4, 0),E(0, 2). 所以S△BCE=. (3)如图2,抛物线的对称轴是直线x=1,当H落在线段EC上时,BH+EH最小. 设对称轴与x轴的交点为P,那么. 因此.解得.所以点H的坐标为. (4)①如图3,过点B作EC的平行线交抛物线于F,过点F作FF′⊥x轴于F′. 由于∠BCE=∠FBC,所以当,即时,△BCE∽△FBC. 设点F的坐标为,由,得. 解得x=m+2.所以F′(m+2, 0). 由,得.所以. 由,得. 整理,得0=16.此方程无解. 图2 图3 图4 ②如图4,作∠CBF=45°交抛物线于F,过点F作FF′⊥x轴于F′, 由于∠EBC=∠CBF,所以,即时,△BCE∽△BFC. 在Rt△BFF′中,由FF′=BF′,得. 解得x=2m.所以F′.所以BF′=2m+2,. 由,得.解得. 综合①、②,符合题意的m为. 例5:如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3). (1)直接写出抛物线的对称轴、解析式及顶点M的坐标; (2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、 B1的坐标分别为 (x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标; (3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由. 图1 图2 思路点拨 1.第(2)题用含S的代数式表示x2-x1,我们反其道而行之,用x1,x2表示S.再注意平移过程中梯形的高保持不变,即y2-y1=3.通过代数变形就可以了. 2.第(3)题最大的障碍在于画示意图,在没有计算结果的情况下,无法画出准确的位置关系,因此本题的策略是先假设,再说理计算,后验证. 3.第(3)题的示意图,不变的关系是:直线AB与x轴的夹角不变,直线AB与抛物线的对称轴的夹角不变.变化的直线PQ的斜率,因此假设直线PQ与AB的交点G在x轴的下方,或者假设交点G在x轴的上方. 满分解答 (1)抛物线的对称轴为直线,解析式为,顶点为M(1,). (2) 梯形O1A1B1C1的面积,由此得到.由于,所以.整理,得.因此得到. 当S=36时, 解得 此时点A1的坐标为(6,3). (3)设直线AB与PQ交于点G,直线AB与抛物线的对称轴交于点E,直线PQ与x轴交于点F,那么要探求相似的△GAF与△GQE,有一个公共角∠G. 在△GEQ中,∠GEQ是直线AB与抛物线对称轴的夹角,为定值. 在△GAF中,∠GAF是直线AB与x轴的夹角,也为定值,而且∠GEQ≠∠GAF. 因此只存在∠GQE=∠GAF的可能,△GQE∽△GAF.这时∠GAF=∠GQE=∠PQD. 由于,,所以.解得. 图3 图4 例6:如图1,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点. (1)求此抛物线的解析式; (2)P是抛物线上的一个动点,过P作PM⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的 点P的坐标;若不存在,请说明理由; (3)在直线AC上方的抛物线是有一点D,使得△DCA的面积最大,求出点D的坐标. , 图1 思路点拨 1.已知抛物线与x轴的两个交点,用待定系数法求解析式时,设交点式比较简便. 2.数形结合,用解析式表示图象上点的坐标,用点的坐标表示线段的长. 3.按照两条直角边对应成比例,分两种情况列方程. 4.把△DCA可以分割为共底的两个三角形,高的和等于OA. 满分解答 (1)因为抛物线与x轴交于A(4,0)、B(1,0)两点,设抛物线的解析式为,代入点C的 坐标(0,-2),解得.所以抛物线的解析式为. (2)设点P的坐标为. ①如图2,当点P在x轴上方时,1<x<4,,. 如果,那么.解得不合题意. 如果,那么.解得. 此时点P的坐标为(2,1). ②如图3,当点P在点A的右侧时,x>4,,. 解方程,得.此时点P的坐标为. 解方程,得不合题意. ③如图4,当点P在点B的左侧时,x<1,,. 解方程,得.此时点P的坐标为. 解方程,得.此时点P与点O重合,不合题意. 综上所述,符合条件的 点P的坐标为(2,1)或或. 图2 图3 图4 (3)如图5,过点D作x轴的垂线交AC于E.直线AC的解析式为. 设点D的横坐标为m,那么点D的坐标为,点E的坐标为.所以. 因此. 当时,△DCA的面积最大,此时点D的坐标为(2,1). 图5 图6查看更多