数学理卷·2017届河南省郑州市一中高三上学期第一次质量检测（2017

数学理卷·2017届河南省郑州市一中高三上学期第一次质量检测（2017

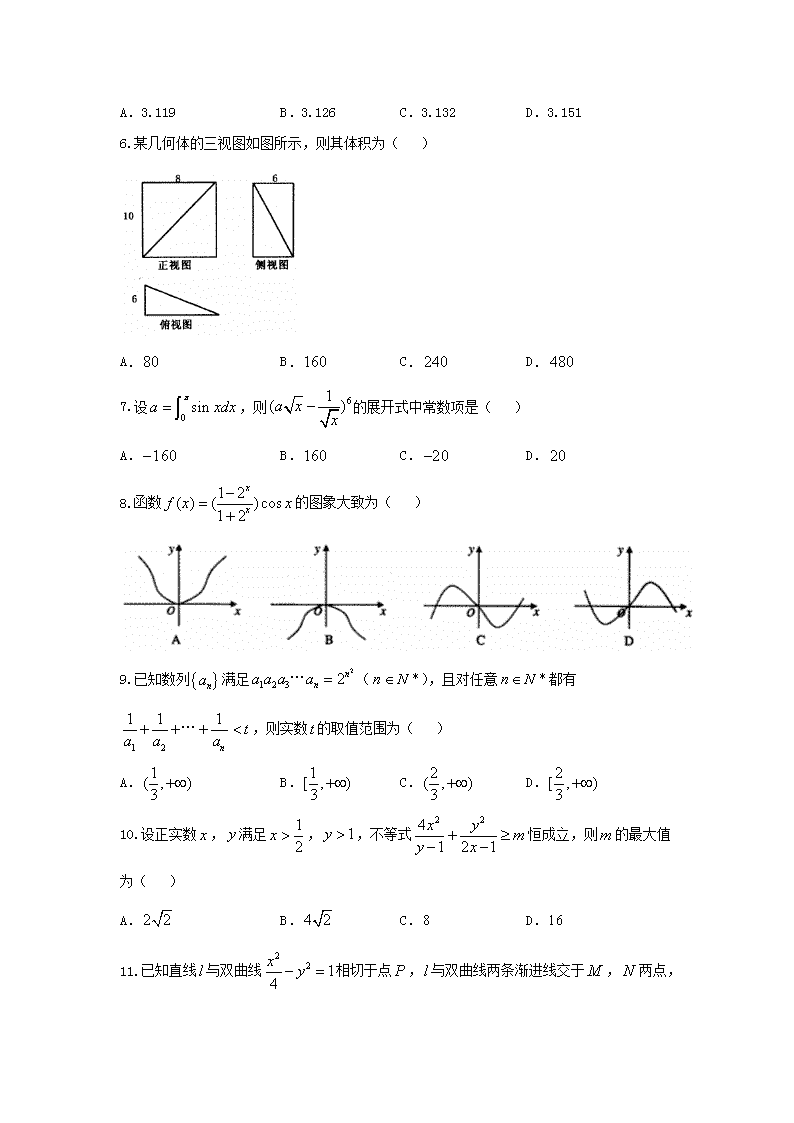
2017 年高中毕业年级第一次质量预测 理科数学 第Ⅰ卷（共 60 分） 一、选择题：本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选 项中，只有一项是符合题目要求的. 1.已知集合  2| 1M x x  ，  | 2 1xN x  ，则 M N  （ ） A． B． | 0 1x x  C． | 0x x  D． | 1x x  2.若复数 z 满足 ( 2 ) 3i z i  （i 为虚数单位），则 z 的共轭复数为（ ） A． 2 i B． 2 i C．1 2i D．1 2i 3.命题“ 0x R  ， 2 0 0 1 0x x   ”的否定是（ ） A． x R  ， 2 1 0x x   B． x R  ， 2 1 0x x   C． 0x R  ， 2 0 0 1 0x x   D． 0x R  ， 2 0 0 1 0x x   4.《张丘建算经》卷上第 22 题为：“今有女善织，日益功疾，且从第 2 天起，每天比前一天 多织相同量的布，若第一天织 5 尺布，现有一月（按 30 天计），共织 390 尺布”，则该女最 后一天织多少尺布？ A．18 B． 20 C． 21 D． 25 5.我们可以用随机模拟的方法估计 的值，如图程序框图表示其基本步骤（函数 RAND 是 产生随机数的函数，它能随机产生 (0,1) 内的任何一个实数）．若输出的结果为521，则由此 可估计 的近似值为（ ） A．3.119 B．3.126 C．3.132 D．3.151 6.某几何体的三视图如图所示，则其体积为（ ） A．80 B．160 C． 240 D． 480 7.设 0 sina xdx    ，则 61( )a x x  的展开式中常数项是（ ） A． 160 B．160 C． 20 D． 20 8.函数 1 2( ) ( )cos1 2 x xf x x  的图象大致为（ ） 9.已知数列 na 满足 2 1 2 3 2n na a a a … （ *n N ），且对任意 *n N 都有 1 2 1 1 1 n ta a a    … ，则实数t 的取值范围为（ ） A． 1( , )3  B． 1[ , )3  C． 2( , )3  D． 2[ , )3  10.设正实数 x ， y 满足 1 2x  ， 1y  ，不等式 2 24 1 2 1 x y my x    恒成立，则 m 的最大值 为（ ） A． 2 2 B． 4 2 C．8 D．16 11.已知直线l 与双曲线 2 2 14 x y  相切于点 P ，l 与双曲线两条渐进线交于 M ， N 两点， 则OM ON  的值为（ ） A．3 B． 4 C．5 D．与 P 的位置有关 12.已知函数 ( ) lnf x x x x  ，若 k Z ，且 ( 1) ( )k x f x  对任意的 1x  恒成立，则 k 的 最大值为（ ） A．2 B．3 C．4 D．5 第Ⅱ卷（共 90 分） 二、填空题（每题 5 分，满分 20 分，将答案填在答题纸上） 13.在平面直角坐标系 xOy 中，已知角 的顶点和点O 重合，始边与 x 轴的非负半轴重合， 终边上一点 M 坐标为 (1, 3) ，则 tan( )4    ． 14.已知实数 x ， y 满足不等式组 3 5 0, 2 4 0, 2 0, x y x y y           则 z x y  的最小值为 ． 15.过抛物线 21 4y x 的焦点 F 作一条倾斜角为30 的直线交抛物线于 A 、 B 两点，则 | |AB  ． 16.若函数 ( )f x 满足 a 、b R ，都有 23 ( ) ( ) 2 ( )3 a bf f a f b   ，且 (1) 1f  ， (4) 7f  ，则 (2017)f  ． 三、解答题 （本大题共 6 小题，共 70 分.解答应写出文字说明、证明过程或演 算步骤.） 17. （本小题满分 12 分） 已知 ABC 外接圆直径为 4 3 3 ，角 A ， B ，C 所对的边分别为 a ，b ， c ， 60C   ． （1）求 sin sin sin a b c A B C     的值； （2）若 a b ab  ，求 ABC 的面积． 18. （本小题满分 12 分） 如图，在四棱锥 S ABCD 中，底面梯形 ABCD 中， / /BC AD ，平面 SAB  平面 ABCD ， SAB 是等边三角形，已知 2 4AC AB  ， 2 2 2 5BC AD CD   ． （1）求证：平面 SAB  平面 SAC ； （2）求二面角 B SC A  的余弦值． 19. （本小题满分 12 分） 北京时间3月15日下午，谷歌围棋人工智能 AlphaGo 与韩国棋手李世石进行最后一轮较量， AlphaGo 获得本场比赛胜利，最终人机大战总比分定格在1: 4 ．人机大战也引发全民对围 棋的关注，某学校社团为调查学生学习围棋的情况，随机抽取了 100 名学生进行调查．根据 调查结果绘制的学生日均学习围棋时间的频率分布直方图（如图所示），将日均学习围棋时 间不低于 40 分钟的学生称为“围棋迷”． （1）根据已知条件完成如图列联表，并据此资料判断你是否有95% 的把握认为“围棋迷” 与性别有关？ （2）将上述调查所得到的频率视为概率．现在从该地区大量学生中，采用随机抽样方法每 次抽取 1 名学生，抽取 3 次，记所抽取的 3 名学生中的“围棋迷”人数为 X ．若每次抽取 的结果是相互独立的，求 X 的分布列，期望 ( )E X 和方差 ( )D X ． 附： 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d      ，其中 n a b c d    ． 2 0( )P x k 0.05 0.010 0k 3.74 6.63 20. （本小题满分 12 分） 已知圆 M ： 2 2 2x y r  （ 0r  ）与直线 1l ： 3 4 0x y   相切，设点 A 为圆上一动点， AB x 轴于 B ，且动点 N 满足 2AB NB  ，设动点 N 的轨迹为曲线C ． （1）求曲线C 的方程； （2）直线l 与直线 1l 垂直且与曲线C 交于 P ，Q 两点，求 OPQ 面积的最大值． 21. （本小题满分 12 分） 设函数 ( ) (1 )ln(1 )f x mx x   ． （1）若当 0 1x  时，函数 ( )f x 的图象恒在直线 y x 上方，求实数 m 的取值范围； （2）求证： 1000.41001( )1000e  ． 请考生在 22、23 两题中任选一题作答，如果多做，则按所做的第一题记分. 22. （本小题满分 10 分）选修 4-4：坐标系与参数方程 在平面直角坐标系 xOy 中，曲线 1C 的参数方程为 2cos sin x y      （ 为参数），在以坐标原点 O 为极点，以 x 轴正半轴为极轴的极坐标系中，曲线 2C 是圆心为 (3, )2  ，半径为 1 的圆． （1）求曲线 1C ， 2C 的直角坐标方程； （2）设 M 为曲线 1C 上的点， N 为曲线 2C 上的点，求| |MN 的取值范围． 23. （本小题满分 10 分）选修 4-5：不等式选讲 已知 0a  ， 0b  ，函数 ( ) | | | |f x x a x b    的最小值为 4． （1）求 a b 的值； （2）求 2 21 1 4 9a b 的最小值． 2017 年高中毕业年级第一次质量预测理科数学试题卷答案 一、选择题 1-5: BDACB 6-10: BACDC 11、12： AB 二、填空题 13. 2 3  14. 13 15.16 3 16. 4033 三、解答题 17.解：（1）由正弦定理可得： 4 32sin sin sin 3 a b c RA B C     ， 所以 4 3 3a  sin A ， 4 3 sin3b B ， 4 3 sin .3 c C 4 3(sin sin sin ) 4 3 sin sin sin 3(sin sin sin ) 3 a b c A B C A B C A B C         ． （2）由 4 3 sin3c C ，得 4 3 3 2,3 2   c 由余弦定理得 2 2 2 2 cosc a b ab C   ，即 2 2 24 ( ) 3a b ab a b ab      ， 又 a b ab  ，所以 2( ) 3 4 0ab ab   ，解得 4ab  或 1ab   （舍去）． 所以 1 1 3sin 4 32 2 2ABCS ab C      ． 18.（1）证明：在 BCA 中，由于 2, 4, 2 5AB CA BC   , ∴ 2 2 2AB AC BC  ,故 AB AC ． 又 SAB ABCD平面 平面 ， SAB ABCD AB平面 平面 ， AC ABCD 平面 ，∴ AC  平面 SAB ， 又 AC SAC 平面 ，故平面 SAC  平面 SAB ． （2）如图建立 A xyz 空间直角坐标系，  0,0,0A ，  2,0,0B ，  1,0, 3S ， (0 4 0)C ，， ， (1 4 3)CS   ， ， ， ( 2 4 0)BC   ，， ，  0,4,0AC  ． 设平面 SBC 的法向量  1 1 1, ,n x y z , 由 1 1 1 1 1 2 4 00 4 3 00 x yn BC x y zn CS                  令 1 1 1 2 31, 2, 3y x z  则 , ∴ 2 32,1, 3n        ． 设平面 SCA 的法向量  2 2 2, ,m x y z , 由 2 2 2 2 4 00 4 3 00 ym AC x y zm CS                ，令 2 3x   ，∴  3,0,1m   ． 2 19cos , 19 n m n m n m           ，∴二面角 - -B SC A 的余弦值为 2 19 19 19.解：（1）由频率分布直方图可知，在抽取的 100 人中，“围棋迷”有 25 人， 从而 2 2 列联表如下： 非围棋迷 围棋迷 合计 男 30 15 45 女 45 10 55 合计 75 25 100 将 2 2 列联表中的数据代入公式计算，得 2 2 2 ( ) 100(30 10 45 15) 100 3.030( )( )( )( ) 75 25 45 55 33 n ad bcK a b c d a c b d              因为 3.030<3.841，所以没有理由认为“围棋迷”与性别有关． （2）由频率分布直方图知抽到“围棋迷”的频率为 0. 25，将频率视为概率，即从观众中抽 取一名“围棋迷”的概率为 1 4 .由题意 13, 3X B     ，从而 X 的分布列为 X 0 1 2 3 P 27 64 27 64 9 64 1 64 1 3( ) 3 4 4E X np    ， 1 3 9( ) 3 4 4 16D X     ． 20.解：（1）设动点 ),( yxN ， ),,( 00 yxA 因为 xAB  轴于 B ，所以 )0,( 0xB ， 设圆 M 的方程为 2 2 2: , M x y r 由题意得 4 2 1 3 r    ， 所以圆 M 的程为 2 2: 4M x y  . 由题意, 2AB NB  ，所以 0 0(0, ) 2( , )y x x y    ， 所以，即 0 0 , 2 ,    x x y y 将 ( ,2 )A x y 代入圆 2 2: 4M x y  ,得动点 N 的轨迹方程 2 2 14 x y  ， (Ⅱ)由题意设直线 l 3 0,  x y m 设直线l 与椭圆交于 2 2 1,4  x y 1 1 2 2( , ), ( , )P x y Q x y ，联立方程 2 2 3 , 4 4,       y x m x y 得 2 213 8 3 4 4 0x mx m    ， 2 2 2192 4 13(4 4) 16( 13) 0m m m         ，解得 2 13m  ， 2 2 1,2 8 3 16( 13) 4 3 2 13 26 13 m m m mx         ， 又因为点 O 到直线l 的距离 2 md  ， 2 1 2 4 132 2 ,13 mPQ x x     2 22 2 (13 )1 4 132 12 2 13 13OPQ m m mmS      . OPQ 面积的最大值为1． 21. 解 ： （ Ⅰ ） 令 ( ) ( ) (1 )ln(1 )F x f x x mx x x      ， 则 1'( ) ln(1 ) 11 mxF x m x x      ， (0,1)x ， 2 2 1"( ) ,(1 )     mx mF x x ①当 1 2m   时，由于 (0,1)x ，有 2 2 1"( ) 0(1 ) mx mF x x     ， 于是 '( )F x 在 (0,1)x 上单调递增，从而 '( ) '(0) 0F x F  ，因此 ( )F x 在 (0,1)x 上单调 递增，即 ( ) 0F x  ； ②当 0m  时，由于 (0,1)x ，有 2 2 1"( ) 0(1 ) mx mF x x     ， 于是 '( )F x 在 (0,1)x 上单调递减，从而 '( ) '(0) 0F x F  ， 因此 ( )F x 在 (0,1)x 上单调递减，即 ( ) (0) 0F x F  不符； ③当 1 02 m   时，令 0 2 1min{1, }mx m   ，当 0(0, ]x x 时， 2 2 1"( ) 0(1 ) mx mF x x     ，于是 '( )F x 在 0(0, ]x x 上单调递减， 从而 '( ) '(0) 0F x F  ，因此 ( )F x 在 0(0, ]x x 上单调递减， 即 ( ) (0) 0F x F  而且仅有 (0) 0F  不符. 综上可知，所求实数 m 的取值范围是 1( , ]2   . (Ⅱ)对要证明的不等式等价变形如下： 对于任意的正整数 n ，不等式 2 51(1 ) n en    恒成立，等价变形 2 1 1(1 )ln(1 ) 05n n n     相当于（2）中 2 5m   ， 0 1 2x  的情形， ( )F x 在 1(0, ]2x 上单调递减，即 ( ) (0) 0F x F  ； 取 1 ( 2)x nn   ，得：都有 2 1 1(1 )ln(1 ) 05n n n     成立； 令 1000n  得证． 22.解：（1）消去参数 可得 1C 的直角坐标方程为 2 2 14  x y . 曲线 2C 的圆心的直角坐标为 )3,0( ， ∴ 2C 的直角坐标方程为 1)3( 22  yx ． （2）设 ),sin,cos2( M 则 22 2 )3(sin)cos2(||  MC 9sin6sincos4 22   13sin6sin3 2   16)1(sin3 2   .  1sin1   ，∴ ,2|| min2 MC ， 4|| max2 MC . 根据题意可得 ,112|| min MN ， ,514|| max MN 即 || MN 的取值范围是 1,5 ． 23. 解：（1）因为， bababxax  ， 所以 ( )f x a b  ，当且仅当 0))((  bxax 时，等号成立，又 0, 0a b> > ， 所以| |a b a b+ = + ，所以 ( )f x 的最小值为 a b ,所以 4a b  ． （2）由（1）知 4, 4a b b a+ = = - ，  22 2 2 2 21 1 1 1 13 8 16 13 16 164 ( )4 9 4 9 36 9 9 36 13 13          a b a a a a a , 当且仅当 16 36,13 13a b= = 时， 2 21 1 4 9a b+ 的最小值为16 13 ．