中考数学几何图形折叠试题典题及解答

中考数学几何图形折叠试题典题及解答

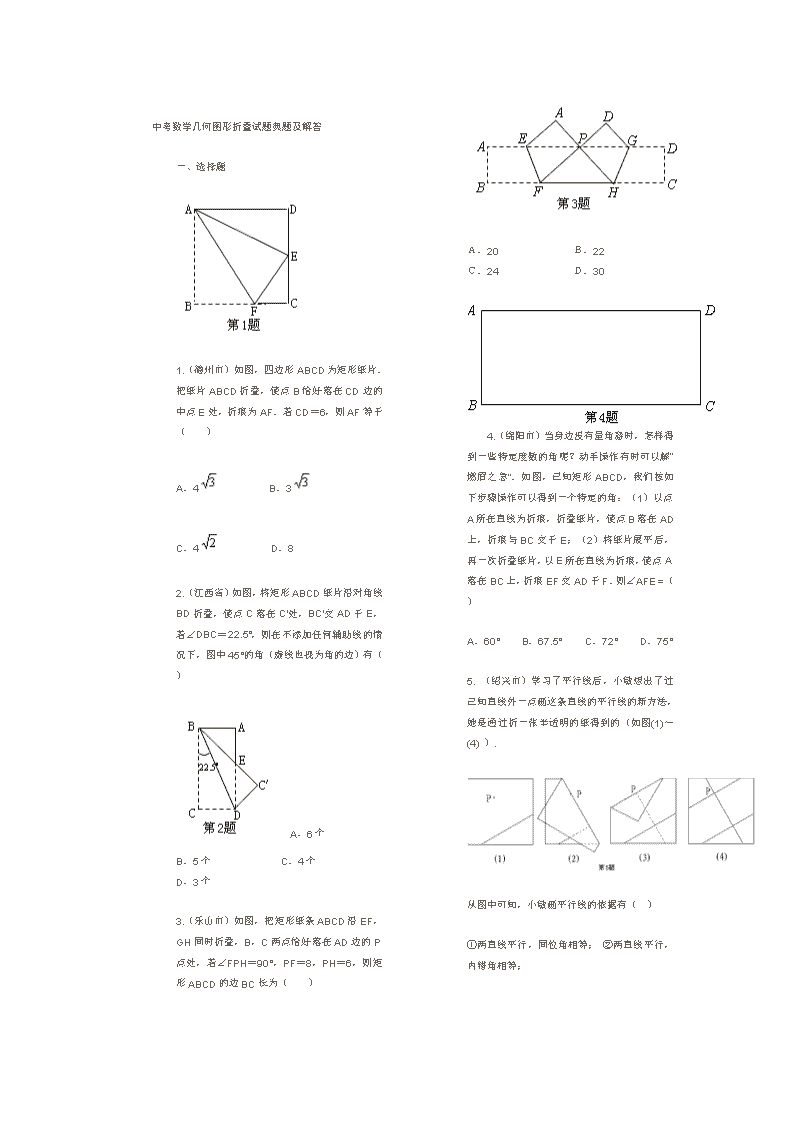
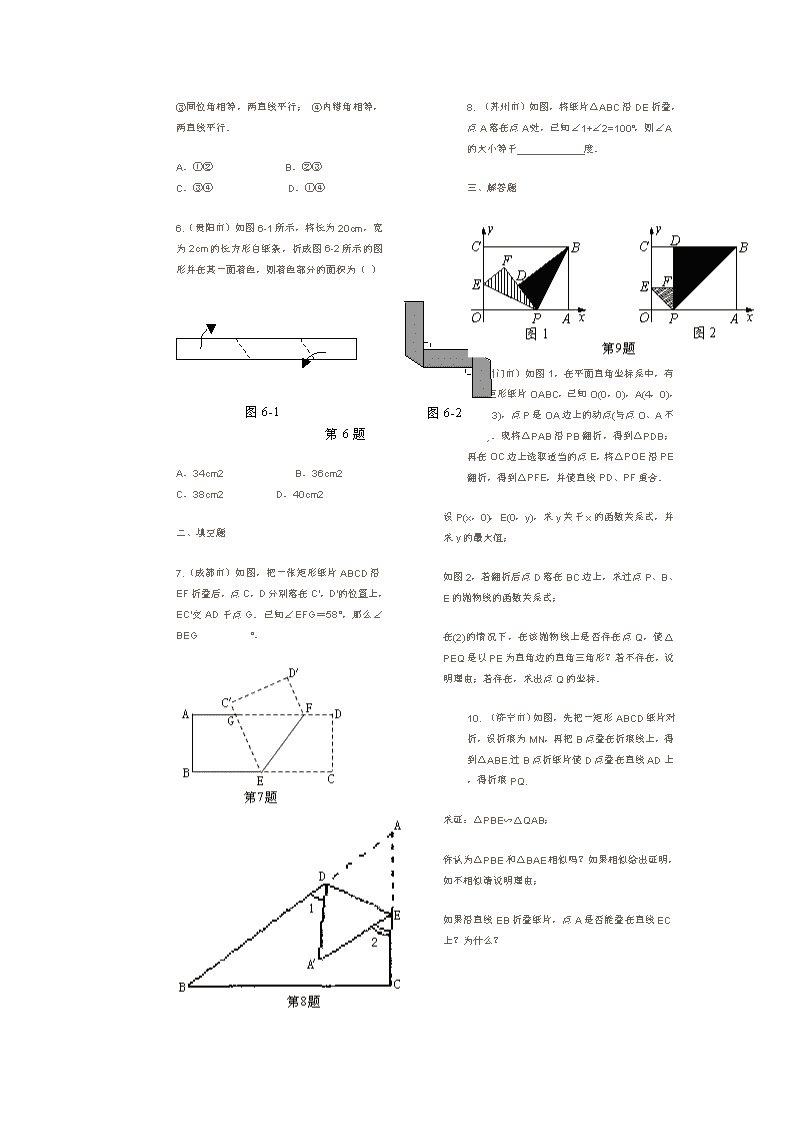
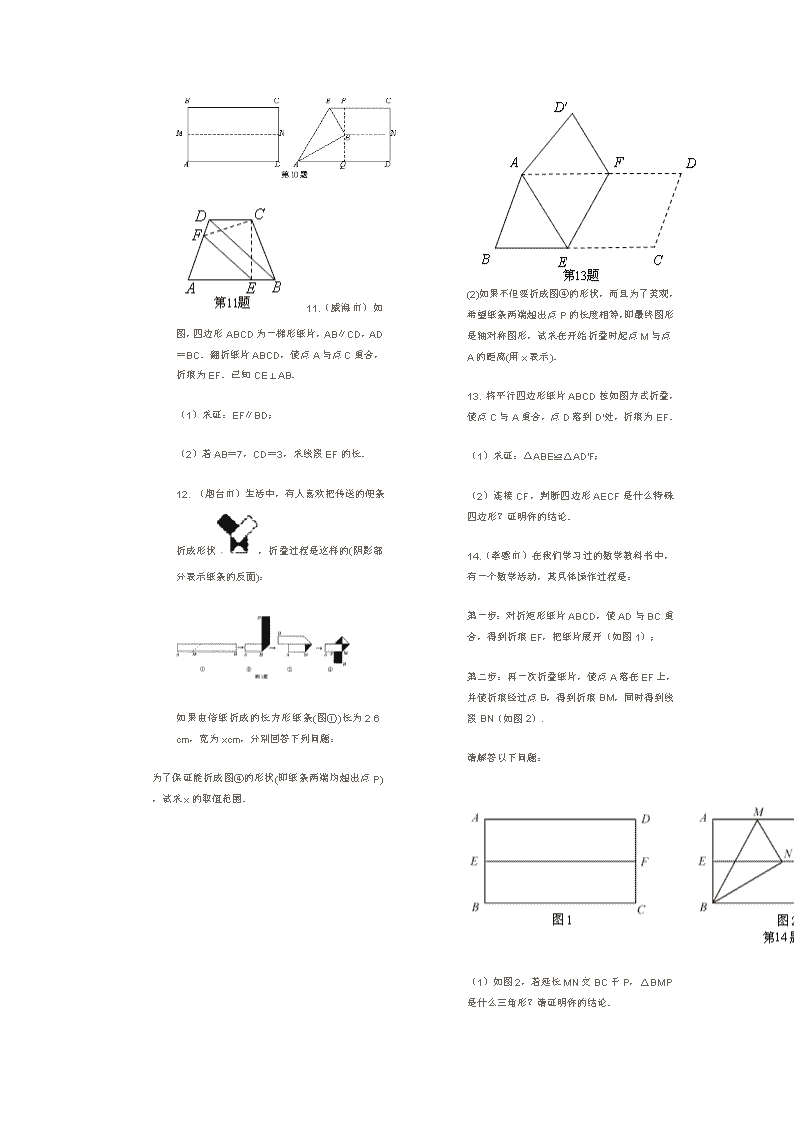
中考数学几何图形折叠试题典题及解答 一、选择题 ‎1.（德州市）如图，四边形ABCD为矩形纸片．把纸片ABCD折叠，使点B恰好落在CD边的中点E处，折痕为AF．若CD＝6，则AF等于（　　）‎ A．4　　　　　B．3‎ C．4　　　　　D．8‎ ‎2.（江西省）如图，将矩形ABCD纸片沿对角线BD折叠，使点C落在C′处，BC′交AD于E，若∠DBC＝22.5°，则在不添加任何辅助线的情况下，图中45°的角（虚线也视为角的边）有（ ）‎ ‎　　A．6个　　　　　　　B．5个　　　　　　　C．4个　　　　　　　D．3个 ‎3.（乐山市）如图，把矩形纸条ABCD沿EF，GH同时折叠，B，C两点恰好落在AD边的P点处，若∠FPH＝90°，PF＝8，PH＝6，则矩形ABCD的边BC长为（　　）‎ Ａ．20　　　　　　　 Ｂ．22　　　　　　　 Ｃ．24　　　　　　　 Ｄ．30‎ ‎　　4.（绵阳市）当身边没有量角器时，怎样得到一些特定度数的角呢？动手操作有时可以解“燃眉之急”．如图，已知矩形ABCD，我们按如下步骤操作可以得到一个特定的角：（1）以点A所在直线为折痕，折叠纸片，使点B落在AD上，折痕与BC交于E；（2）将纸片展平后，再一次折叠纸片，以E所在直线为折痕，使点A落在BC上，折痕EF交AD于F．则∠AFE =（　）‎ A．60° 　　B．67.5° 　　C．72° 　　D．75°‎ ‎5. （绍兴市）学习了平行线后，小敏想出了过己知直线外一点画这条直线的平行线的新方法，她是通过折一张半透明的纸得到的（如图(1)～(4) ）.‎ 从图中可知，小敏画平行线的依据有（　）‎ ‎①两直线平行，同位角相等； ②两直线平行，内错角相等；‎ ‎③同位角相等，两直线平行； ④内错角相等，两直线平行．‎ A．①②　　　　　　　 B．②③　　　　　　　 C．③④ 　　　　　　　D．①④‎ ‎6.（贵阳市）如图6-1所示，将长为20cm，宽为2cm的长方形白纸条，折成图6-2所示的图形并在其一面着色，则着色部分的面积为（ ）‎ A．34cm2 　　　　　　　B．36cm2 　　　　　　　C．38cm2 　　　　　D．40cm2‎ 二、填空题 ‎7.（成都市）如图，把一张矩形纸片ABCD沿EF折叠后，点C，D分别落在C′，D′的位置上，EC′交AD于点G．已知∠EFG＝58°，那么∠BEG　　　　　 °．‎ ‎　　　　‎ ‎8. （苏州市）如图，将纸片△ABC沿DE折叠，点A落在点A′处，已知∠1+∠2=100°，则∠A的大小等于____________度．‎ 三、解答题 ‎9.（荆门市）如图1，在平面直角坐标系中，有一张矩形纸片OABC，已知O(0，0)，A(4，0)，C(0，3)，点P是OA边上的动点(与点O、A不重合)．现将△PAB沿PB翻折，得到△PDB；再在OC边上选取适当的点E，将△POE沿PE翻折，得到△PFE，并使直线PD、PF重合．‎ 设P(x，0)，E(0，y)，求y关于x的函数关系式，并求y的最大值；‎ 如图2，若翻折后点D落在BC边上，求过点P、B、E的抛物线的函数关系式；‎ 在(2)的情况下，在该抛物线上是否存在点Q，使△PEQ是以PE为直角边的直角三角形？若不存在，说明理由；若存在，求出点Q的坐标．‎ ‎10. （济宁市）如图，先把一矩形ABCD纸片对折，设折痕为MN，再把B点叠在折痕线上，得到△ABE.过B点折纸片使D点叠在直线AD上，得折痕PQ.‎ 求证：△PBE∽△QAB；‎ 你认为△PBE和△BAE相似吗？如果相似给出证明，如不相似请说明理由；‎ 如果沿直线EB折叠纸片，点A是否能叠在直线EC上？为什么？‎ ‎　　11.（威海市）如图，四边形ABCD为一梯形纸片，AB∥CD，AD＝BC．翻折纸片ABCD，使点A与点C重合，折痕为EF．已知CE⊥AB．‎ ‎（1）求证：EF∥BD；‎ ‎（2）若AB＝7，CD＝3，求线段EF的长．‎ ‎12. （烟台市）生活中，有人喜欢把传送的便条折成形状，折叠过程是这样的(阴影部分表示纸条的反面)：‎ 如果由信纸折成的长方形纸条(图①)长为2 6 cm，宽为xcm，分别回答下列问题：‎ 为了保证能折成图④的形状(即纸条两端均超出点P)，试求x的取值范围．‎ ‎(2)如果不但要折成图④的形状，而且为了美观，希望纸条两端超出点P的长度相等，即最终图形是轴对称图形，试求在开始折叠时起点M与点A的距离(用x表示)．‎ ‎13. 将平行四边形纸片ABCD按如图方式折叠，使点C与A重合，点D落到D′处，折痕为EF．‎ ‎（1）求证：△ABE≌△AD′F；‎ ‎（2）连接CF，判断四边形AECF是什么特殊四边形？证明你的结论．‎ ‎14.（孝感市）在我们学习过的数学教科书中，有一个数学活动，其具体操作过程是：‎ 第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开（如图1）；‎ 第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2）.‎ 请解答以下问题：‎ ‎（1）如图2，若延长MN交BC于P，△BMP是什么三角形？请证明你的结论．‎ ‎（2）在图2中，若AB=a，BC=b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合（1）中结论的三角形纸片BMP ？‎ ‎（3）设矩形ABCD的边AB=2，BC=4，并建立如图3所示的直角坐标系. 设直线BM′为y=kx，当∠M′BC=60°时，求k的值.此时，将△ABM′沿BM′折叠，点A是否落在EF上（E、F分别为AB、CD中点）？为什么？‎ ‎15.（邵阳市）如图①，△ABC中，∠ACB=90°，将△ABC沿着一条直线折叠后，使点A与点C重合（图②）．‎ ‎（1）在图①中画出折痕所在的直线l．设直线l与AB,AC分别相交于点D,E，连结CD．（画图工具不限，不要求写画法）‎ ‎（2）请你找出完成问题（1）后所得到的图形中的等腰三角形．（不要求证明）‎ ‎16.（济宁市）如图，先把一矩形ABCD纸片对折，设折痕为MN，再把B点叠在折痕线上，得到△ABE.过B点折纸片使D点叠在直线AD上，得折痕PQ.‎ 求证：△PBE∽△QAB；‎ 你认为△PBE和△BAE相似吗？如果相似给出证明，如补相似请说明理由；‎ ‎(3)如果直线EB折叠纸片，点A是否能叠在直线EC上？为什么？‎ ‎17.（临安市）如图，△OAB是边长为的等边三角形，其中O是坐标原点，顶点B在y轴正方向上，将△OAB 折叠，使点A落在边OB上，记为A′，折痕为EF.‎ ‎（1）当A′E//x轴时，求点A′和E的坐标；‎ ‎（2）当A′E//x轴，且抛物线经过点A′和E时，求抛物线与x轴的交点的坐标；‎ ‎（3）当点A′在OB上运动，但不与点O、B重合时，能否使△A′EF成为直角三角形？若能，请求出此时点A′的坐标；若不能，请你说明理由.‎ ‎18.（南宁市）如图，在锐角△ABC中，BC=9，AH⊥BC于点H，且AH=6，点D为AB边上的任意一点，过点D作DE∥BC，交AC于点E．设△ADE的高AF为x(0＜x＜6），以DE为折线将△ADE翻折，所得的△A′DE与梯形DBCE重叠部分的面积记为y（点A关于DE的对称点A′落在AH所在的直线上）．‎ ‎（1）分别求出当0＜x≤3与3＜x＜6时，y与x的函数关系式；‎ ‎（2）当x取何值时，y的值最大？最大值是多少？‎ ‎19.（宁夏回族自治区）如图，将矩形纸片ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，连结AE．证明：‎ ‎（1）BF=DF；‎ ‎（2）AE∥BD．‎ 参考答案 一、1.A　2.B　3.C　4.B　5.C　6.B 二、7.64　8.50°‎ 三、9. 解：(1)由已知PB平分∠APD，PE平分∠OPF，且PD、PF重合，则∠OPE＋∠APB=90°．‎ 又∠APB＋∠ABP=90°，∴∠OPE=∠PBA．‎ ‎∴Rt△POE∽Rt△BPA．‎ ‎∴.即．∴．‎ 且当x=2时，y有最大值．‎ 由已知，△PAB、△POE均为等腰直角三角形，可得P(1，0)，E(0，1)，B(4，3)．……6分 设过此三点的抛物线为y=ax2＋bx＋c，则∴‎ y=．‎ 由(2)知∠EPB=90°，即点Q与点B重合时满足条件．‎ 直线PB为y=x－1，与y轴交于点(0，－1)．‎ 将PB向上平移2个单位则过点E(0，1)，‎ ‎∴该直线为y=x＋1．‎ 由得∴Q(5，6)．‎ 故该抛物线上存在两点Q(4，3)、(5，6)满足条件．‎ ‎10. 证明：（1）∵∠PBE＋∠ABQ＝180°－90°＝90°，∠PBE＋∠PEB＝90°，‎ ‎∴∠ABQ＝∠PEB.‎ 又∵∠BPE＝∠AQB＝90°，∴△PBE～△QAB.‎ ‎（2）∵△PBE～△QAB，∴‎ ‎∵BQ＝PB，∴.‎ 又∵∠ABE＝∠BPE＝90°，∴△PBE～△BAE.‎ ‎（3）点A能叠在直线EC上.由（2）得，∠AEB＝∠CEB，∴EC和折痕AE重合.‎ ‎11. 解：(1）证明：过C点作CH∥BD，交AB的延长线于点H；‎ 连结AC，交EF于点K，则AK＝CK．‎ ‎∵AB∥CD，‎ ‎∴BH＝CD，BD＝CH．‎ ‎∵AD＝BC，‎ ‎∴AC＝BD＝CH．‎ ‎∵CE⊥AB，‎ ‎∴AE＝EH．‎ ‎∴EK是△AHC的中位线．‎ ‎∴EK∥CH．‎ ‎∴EF∥BD．‎ ‎（2）解：由（1）得BH∥CD，EF∥BD，‎ ‎∴∠AEF＝∠ABD．‎ ‎∵AB＝7，CD＝3，‎ ‎∴AH＝10．‎ ‎∵AE＝CE，AE＝EH，‎ ‎∴AE＝CE＝EH＝5.‎ ‎∵CE⊥AB，‎ ‎∴CH＝5＝BD．‎ ‎∵∠EAF＝∠BAD，∠AEF＝∠ABD，‎ ‎∴△AFE∽△ADB．‎ ‎∴.‎ ‎∴．‎ ‎12. 解：(1)由折纸过程知0＜5x＜26，,0＜x＜.‎ ‎（2）图④为轴对称图形，∴AM＝.即点M与点A的距离是（13－x）cm.‎ ‎13. 证明：⑴ 由折叠可知：∠D＝∠D′，CD＝AD′，∠C＝∠D′AE．‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴∠B＝∠D，AB＝CD，∠C＝∠BAD．‎ ‎∴∠B＝∠D′，AB＝AD′，‎ ‎∠D′AE＝∠BAD，即∠1＋∠2＝∠2＋∠3．‎ ‎∴∠1＝∠3．‎ ‎∴△ABE ≌△AD′F．‎ ‎⑵ 四边形AECF是菱形．‎ 由折叠可知AE＝EC，∠4＝∠5．‎ ‎∵四边形ABCD是平行四边形，∴AD∥BC．‎ ‎∴∠5＝∠6．∴∠4＝∠6．∴AF＝AE．‎ ‎∵AE＝EC， ∴AF＝EC．‎ 又∵AF∥EC，‎ ‎∴四边形AECF是平行四边形．‎ ‎∵AF＝AE，‎ ‎∴四边形AECF是菱形．‎ ‎14. 解：（1）△BMP是等边三角形.‎ 证明：连结AN.‎ ‎∵EF垂直平分AB，∴AN = BN.‎ 由折叠知 AB = BN ，‎ ‎∴AN = AB = BN， ∴△ABN为等边三角形.‎ ‎∴∠ABN =60°. ∴∠PBN =30°.‎ 又∵∠ABM =∠NBM =30°，∠BNM =∠A =90°.‎ ‎∴∠BPN =60°.‎ ‎∠MBP =∠MBN +∠PBN =60°.‎ ‎∴∠BMP =60°‎ ‎∴∠MBP =∠BMP =∠BPM =60°.‎ ‎∴△BMP为等边三角形 .‎ ‎（2）要在矩形纸片ABCD上剪出等边△BMP，则BC ≥BP.‎ 在Rt△BNP中， BN = BA =a，∠PBN =30°，‎ ‎∴BP =. ∴b≥. ∴a≤b .‎ ‎∴当a≤b时，在矩形上能剪出这样的等边△BMP.‎ ‎（3）∵∠M′BC =60°， ∴∠ABM′=90°－60°=30°.‎ 在Rt△ABM′中，tan∠ABM′ =. ∴tan30°=. ∴AM′ =.‎ ‎∴M′(，2). 代入y=kx中 ，得k==.‎ 设△ABM′沿BM′折叠后，点A落在矩形ABCD内的点为A′.‎ 过A′作AH ⊥BC交BC于H.‎ ‎∵△A′BM′ ≌△ABM′， ∴∠A′BM′=∠ABM′=30°, A′B = AB =2.‎ ‎∴∠A′BH＝∠M′BH－∠A′BM′=30°.‎ 在Rt△A′BH中，A′H =A′B =1 ，BH=，‎ ‎∴.‎ ‎∴A'落在EF上.‎ ‎(图2)‎ ‎(图3)‎ ‎15.解：(1)如图.‎ 等腰三角形DAC.‎ ‎16.（1）证明：∵∠PBE＋∠ABQ＝180°-90°＝90°，∠PBE＋∠PEB＝90°，‎ ‎∴∠ABQ＝∠PEB.‎ 又∵∠BPE＝∠AQB，‎ ‎∴△PBE∽△QAB.‎ ‎（2）∵△PBE∽△QAB，‎ ‎∴.‎ ‎∵BQ＝PB，∴.‎ 又∵∠ABE＝∠BPE＝90°，∴△PBE～△BAE.‎ ‎（3）点A能折叠在直线EC上.‎ 由（2）得，∠AEB＝∠CEB，∴EC和折痕AE重合.‎ ‎17. 解：（1）由已知可得∠A'OE=60o , A'E=AE.‎ 由A′E//x轴,得△OA'E是直角三角形.‎ 设A′的坐标为（0，b），则 AE=A'E=b,OE=2b.‎ ‎∵b+2b=2+,‎ ‎∴b=1.∴A'、E的坐标分别是（0，1）与（，1）.‎ ‎（2）因为A'、E在抛物线上，所以 所以 函数关系式为y=.‎ 由=0得, .‎ 与x轴的两个交点坐标分别是（-，0）与（，0）.‎ ‎（3）不可能使△A'EF成为直角三角形.‎ ‎∵∠FA'E=∠FAE=60o,若△A'EF成为直角三角形,只能是∠A'EF=90o或∠A'FE=90o.‎ 若∠A'EF=90o,利用对称性,则∠AEF=90o, A'、E、A三点共线，O与A重合，与已知矛盾.‎ 同理若∠A'FE=90o也不可能.‎ 所以不能使△A′EF成为直角三角形.‎ ‎18. 解：（1）①当0＜x≤3时，由折叠得到的△A'ED落在△ABC内部如图10（1），重叠部分为△A'ED.‎ ‎∵DE∥BC,‎ ‎∴∠ADE＝∠B，∠AED＝∠C.‎ ‎∴△ADE∽△ABC.‎ ‎∴. ∴，即.‎ 又∵FA'=FA=x,‎ ‎∴y=DE·A'F=·x·x.‎ ‎∴(0＜x≤3）.‎ ‎②当3＜x＜6时，由折叠得到的△A'ED有一部分落在△ABC外，如图10（2），重叠部分为梯形EDPQ.‎ ‎∵FH＝6－AF＝6－x,‎ A'H＝A'F－FH＝x-(6-x)=2x-6,‎ 又∵DE∥PQ,‎ ‎∴△A'PQ∽△A'DE.‎ ‎∴.‎ ‎∴‎ ‎∴.‎ ‎（2）当0＜x≤3时，y的最大值；‎ 当3＜x＜6时，由,可知当x=4时，y的最大值y2=9.‎ ‎∵y1＜y2，∴当x=4时，y有最大值y最大＝9．‎ ‎19. 证明：（1）能正确说明∠ADB=∠EBD（或△ABF≌△EDF）,‎ ‎∴BF=DF.‎ ‎（2）能得出∠AEB=∠DBE（或∠EAD=∠BDA）,‎ ‎∴AE∥BD.‎