高考数学专题复习课件：4-7 正弦定理、余弦定理

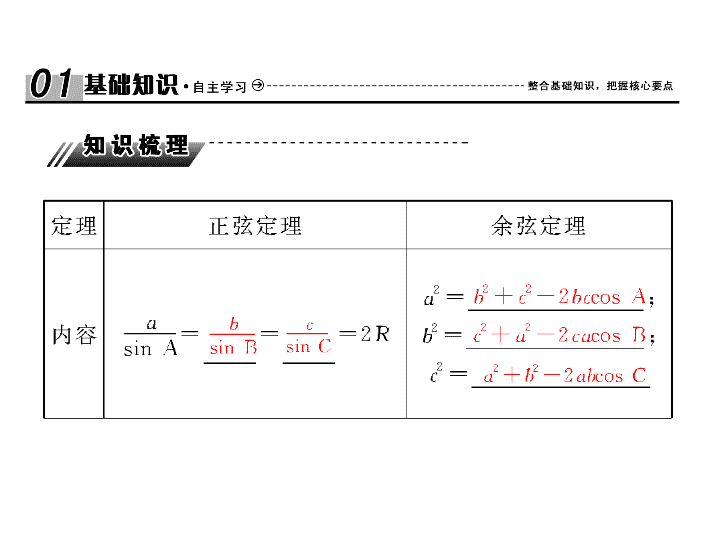
高考数学专题复习课件：4-7 正弦定理、余弦定理

§4.7 　正弦定理、余弦定理 [ 考纲要求 ] 　掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题． 【 思考辨析 】 　判断下面结论是否正确 ( 请在括号中打 “√” 或 “ ×” ) (1) 三角形中三边之比等于相应的三个内角之比． ( 　　 ) (2) 在 △ ABC 中，若 sin A ＞ sin B ，则 A ＞ B .( 　　 ) (3) 在 △ ABC 的六个元素中，已知任意三个元素可求其他元素． ( 　　 ) (4) 当 b 2 ＋ c 2 － a 2 ＞ 0 时，三角形 ABC 为锐角三角形；当 b 2 ＋ c 2 － a 2 ＝ 0 时，三角形为直角三角形；当 b 2 ＋ c 2 － a 2 ＜ 0 时，三角形为钝角三角形． ( 　　 ) (5) 在三角形中，已知两边和一角就能求三角形的面积． ( 　　 ) 【 答案 】 (1) × 　 (2) √ 　 (3) × 　 (4) × 　 (5) √ 【 答案 】 C 【 答案 】 B 【 答案 】 1 【 答案 】 (1)B 　 (2)45 ° ， 30 ° ， 105 ° 　 (3)1 【 方法规律 】 (1) 判断三角形解的个数的两种方法 ① 代数法：根据大边对大角的性质、三角形内角和公式、正弦函数的值域等判断． ② 几何图形法：根据条件画出图形，通过图形直观判断解的个数． (2) 已知三角形的两边和其中一边的对角解三角形．可用正弦定理，也可用余弦定理．用正弦定理时，需判断其解的个数，用余弦定理时，可根据一元二次方程根的情况判断解的个数． 【 答案 】 (1)A 　 (2)C 题型三　正弦、余弦定理的简单应用 命题点 1 　判断三角形的形状 【 例 3 】 (1) (2017· 辽宁省实验中学分校期中 ) 已知 △ ABC 中， sin A (cos B ＋ cos C ) ＝ sin B ＋ sin C ，则这个三角形是 ( 　　 ) A ．直角三角形 B ．等腰三角形 C ．等腰直角三角形 D ．以上都不对 (2) (2016· 贵州贵阳一中第四次月考 ) 如果把直角三角形的三边都增加同样的长度，则得到的这个新三角形的形状为 ( 　　 ) A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．由增加的长度决定 【 解析 】 (1) 由已知等式，得 sin A cos B ＋ sin A · cos C ＝ sin( A ＋ C ) ＋ sin( A ＋ B ) ＝ sin A · cos C ＋ cos A sin C ＋ sin A cos B ＋ cos A sin B ，所以 cos A (sin C ＋ sin B ) ＝ 0 ，则 cos A ＝ 0 ，于是由 0 ＜ A ＜ π ，得 A ＝，所以 △ ABC 为直角三角形．故选 A. (2) 设增加的同样的长度为 x ，原三边长为 a ， b ， c ，且 c 2 ＝ a 2 ＋ b 2 ， a ＋ b ＞ c ，新的三角形的三边长为 a ＋ x ， b ＋ x ， c ＋ x ，知 c ＋ x 为最大边，其对应角最大．而 ( a ＋ x ) 2 ＋ ( b ＋ x ) 2 － ( c ＋ x ) 2 ＝ x 2 ＋ 2( a ＋ b － c ) x ＞ 0 ，由余弦定理知新的三角形的最大角的余弦值为正，则最大角为锐角，那么它为锐角三角形．故选 A. 【 答案 】 (1)A 　 (2)A 【 方法规律 】 (1) 判断三角形形状的方法 ① 化边：通过因式分解、配方等得出边的相应关系，从而判断三角形的形状； ② 化角：通过三角恒等变形，得出内角的关系，从而判断三角形的形状，此时要注意应用 A ＋ B ＋ C ＝ π 这个结论． (2) 求解几何计算问题要注意 ① 根据已知的边角画出图形并在图中标示； ② 选择在某个三角形中运用正弦定理或余弦定理． 【 温馨提醒 】 (1) 本题将正弦定理、余弦定理和和差公式综合进行考查，具有一定的综合性，要求考生对公式要熟练记忆；通过审题理清解题方向； (2) 本题还考查考生的基本运算求解能力，要求计算准确无误，尽量简化计算过程，减少错误 . ► 失误与防范 1 ．在利用正弦定理解已知三角形的两边和其中一边的对角求另一边的对角，进而求出其他的边和角时，有时可能出现一解、两解，所以要进行分类讨论． 2 ．在解三角形或判断三角形形状时，要注意三角函数值的符号和角的范围，防止出现增解、漏解 .