- 2021-04-22 发布 |
- 37.5 KB |
- 12页

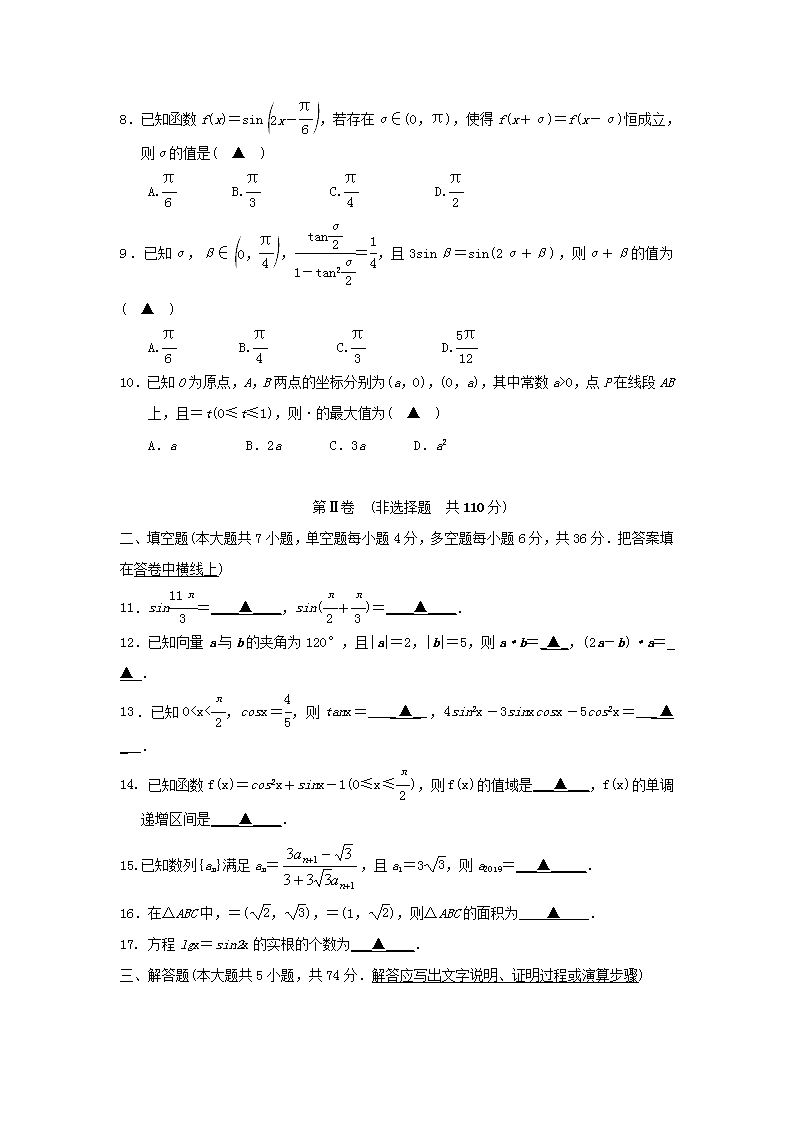

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年浙江省杭州市西湖高级中学高一4月月考数学试题
2018-2019学年浙江省杭州市西湖高级中学高一4月月考数学试题 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷40分,第Ⅱ卷110分,共150分,考试时间120分钟. 第Ⅰ卷 (选择题 共40分) 一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知角α的终边经过点P(4,-3),则2sinα+cosα的值为( ▲ ) A.- B. C. D.- 2.已知向量e1=(1,0),e2=(0,1),那么|e1+2e2|=( ▲ ) A.1 B. C.2 D. 3.函数y=cosx·tanx的值域是( ▲ ) A.(-1,0)∪(0,1) B.[-1,1] C.(-1,1) D.[-1,0)∪(0,1] 4.已知角C为△ABC的一个内角,向量m=(2cosC-1,-2),n=(cosC,cosC+1).若 m⊥n,则角C等于( ▲ ) A. B. C. D. 5.在△ABC中,A=15°,则sinA-cos(B+C)的值为( ▲ ) A. B. C. D.2 6.函数f(x)=tan的单调递增区间为( ▲ ) A.(k∈Z) B.(k∈Z) C.(k∈Z) D.(k∈Z) 7.函数y=在一个周期内的图像大致是(▲) 8.已知函数f(x)=sin,若存在α∈(0,π),使得f(x+α)=f(x-α)恒成立,则α的值是( ▲ ) A. B. C. D. 9.已知α,β∈,=,且3sinβ=sin(2α+β),则α+β的值为( ▲ ) A. B. C. D. 10.已知O为原点,A,B两点的坐标分别为(a,0),(0,a),其中常数a>0,点P在线段AB上,且=t(0≤t≤1),则·的最大值为( ▲ ) A.a B.2a C.3a D.a2 第Ⅱ卷 (非选择题 共110分) 二、填空题(本大题共7小题,单空题每小题4分,多空题每小题6分,共36分.把答案填在答卷中横线上) 11.sin=____▲____,sin(+)=____▲____. 12.已知向量a与b的夹角为120°,且|a|=2,|b|=5,则a·b=_▲_,(2a-b)·a= ▲ . 13.已知0查看更多