- 2021-04-22 发布 |
- 37.5 KB |
- 11页
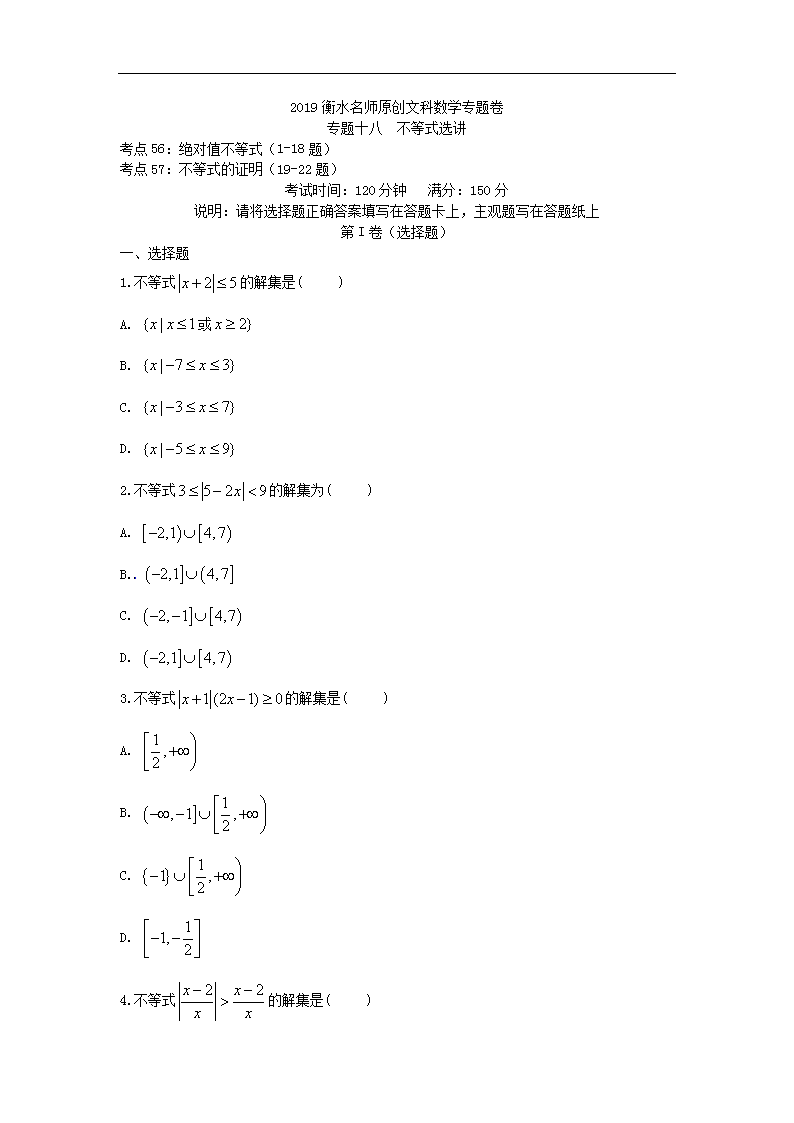


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019衡水名师原创文科数学专题卷专题十八《不等式选讲》
2019衡水名师原创文科数学专题卷 专题十八 不等式选讲 考点56:绝对值不等式(1-18题) 考点57:不等式的证明(19-22题) 考试时间:120分钟 满分:150分 说明:请将选择题正确答案填写在答题卡上,主观题写在答题纸上 第I卷(选择题) 一、选择题 1.不等式的解集是( ) A. 或 B. C. D. 2.不等式的解集为( ) A. B. C. D. 3.不等式的解集是( ) A. B. C. D. 4.不等式的解集是( ) A. B. C. D. 5.设,不等式的解集是, ( ) A. B. C. D. 6.不等式的解集是( ) A. 或 B. C. 或 D. 7.函数的最小值为( ) A. B. C. D. 8.关于的不等式的解集不是空集, 的取值范围是( ) A. B. C. D. 9.对于实数,若,规定,则不等式的解集是( ) A. B. C. D. 10.已知实数,满足,且,则等于( ) A. B. C. D. 11.对一切实数,不等式恒成立,则实数的取值范围是( ) A. B. C. D. 12.设集合若,则实数的取值集合是( ) A. B. 或 C. 或 D. 二、填空题 13.设函数若存在,使得成立,则的取值范围为__________ 14.不等式对任意实数恒成立,则实数的取值范围为______. 15对于任意实数和,不等式恒成立,则实数的取值范围是 . 16.已知函数,若,则实数的取值范围是__________. 三、解答题 17.选修4—5:不等式选讲 已知 1.若,解不等式 2. 在上有解,求实数的取值范围. 18.已知函数 1.当时,求不等式的解集; 2.设函数求的取值范围. 19.设函数 1.当时,解关于的不等式; 2.如果对任意的,不等式恒成立,求的取值范围. 20.根据所学知识,回答下列问题. 1.已知对于任意非零实数和,不等式恒成立,试求实数的取值范围; 2.已知不等式的解集为,若,,试比较与的大小.(并说明理由) 21.已知函数. 1.解不等式; 2.若正数满足,求的最小值. 22.已知,,为正实数,且. 1.解关于的不等式; 2.证明: . 参考答案 一、选择题 1.答案:B 解析: 2.答案:D 解析:本题考查含绝对值不等式的解法原不等式可化为, 由得或,解得或, 由得,解得, 用数轴表示上述不等式有或, 故正确答案为D. 3.答案:C 解析:本题考查绝对值的意义,不等式的解法,等价转化. 因为, 所以不等式可化为或, 解得或, 则不等式的解集是. 故选C 4.答案:A 解析:本题考查绝对值的含义,不等式的解法,等价转化思想. 因为时, ; 时, ,则, 所以不等式可化为, 即,解得,故选A. 5.答案:B 解析: 6.答案:B 解析: 7.答案:C 解析: 8.答案:B 解析:本题考查绝对值不等式的性质及转化思想,分析解决问题的能力. 因为对任意,都有恒成立, 所以要使不等式的解集表示空集,需使.故选B. 9.答案:C 解析:首先正确理解“对于实数,若,,规定",是本题的关键所在.即为取整函数.然后由后边的不等式解除的取值范围,然后把不等式的两边取整.即得到答案. 正确理解"对于实数,若,规定",是本题的关键所在. 先解得, 因为,时, ,所以, 即不等式的解集是. 所以答案为C. 10.答案:B 解析:若实数、满足, 则与异号, 又,故,,则. 11.答案:C 解析:解法一:令,则,∴对恒成立,当时,显然不等式恒成立. 当时, 在上的最小值为,由题意得, 解得,∴,综上,故选C. 解法二: 对一切实数,恒成立. 当时, 恒成立. 当时, 因为的最大值为,故. 考点:恒成立问题,及参数分离法. 12.答案:C 解析:根据绝对值的意义得,若,则或,解得或. 二、填空题 13.答案: 解析: 14.答案: 解析: 答案: [-1,3] 解析: 依题意可得恒成立,等价于小于或等于的最小值. 因为. 所以,∴. 16.答案: 解析:当时, , ∴,恒成立, 当时, , ∴或, ∴或, 综上所述, 的取值范围是. 三、解答题 17.答案:1. 时, ,故,或或, 解得: 或或, 所以原不等式解集为. 2.∵, ∴, 故有解, 所以, ∴不等式化为有解,即. 解析: 18.答案:1.当时, 等价于当时,解得; 当时,解得当时,解得;所以解集为; 2.当时, , 所以当时, 等价于.① 当时,①等价于,无解; 当时,①等价于,解得,所以的取值范围是 解析: 19.答案:1. 即 即等价于, ①当时,不等式等价于 ∴ ②当时,不等式等价于 ∴不等式无解 ③当时,不等式等价于 ∴ 由①②③知不等式解集是或 2.由条件知道只要即可 ∵ (当且仅当取等号) ∴ ∴ ∴或 解析: 20.答案:1. , 当且仅当时取等号, 只需: , 由于,只需, 所以: 的取值范围为: . 2. 解集为,解得: ,,, 知: , 即. 解析: 21.答案:1.不等式的解集为 2. 解析: 22.答案:1.∵且, ∴, ∴, ∴不等式的解集为. 2.∵ (当且仅当时取等号), (当且仅当时取等号), (当且仅当时取等号), ∴, ∴, ∵, ∴. 解析:查看更多