- 2021-04-22 发布 |
- 37.5 KB |
- 20页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
西藏自治区山南市第三高级中学2020届高三第三次模拟考试前自查自测调研考试数学(理)一试卷
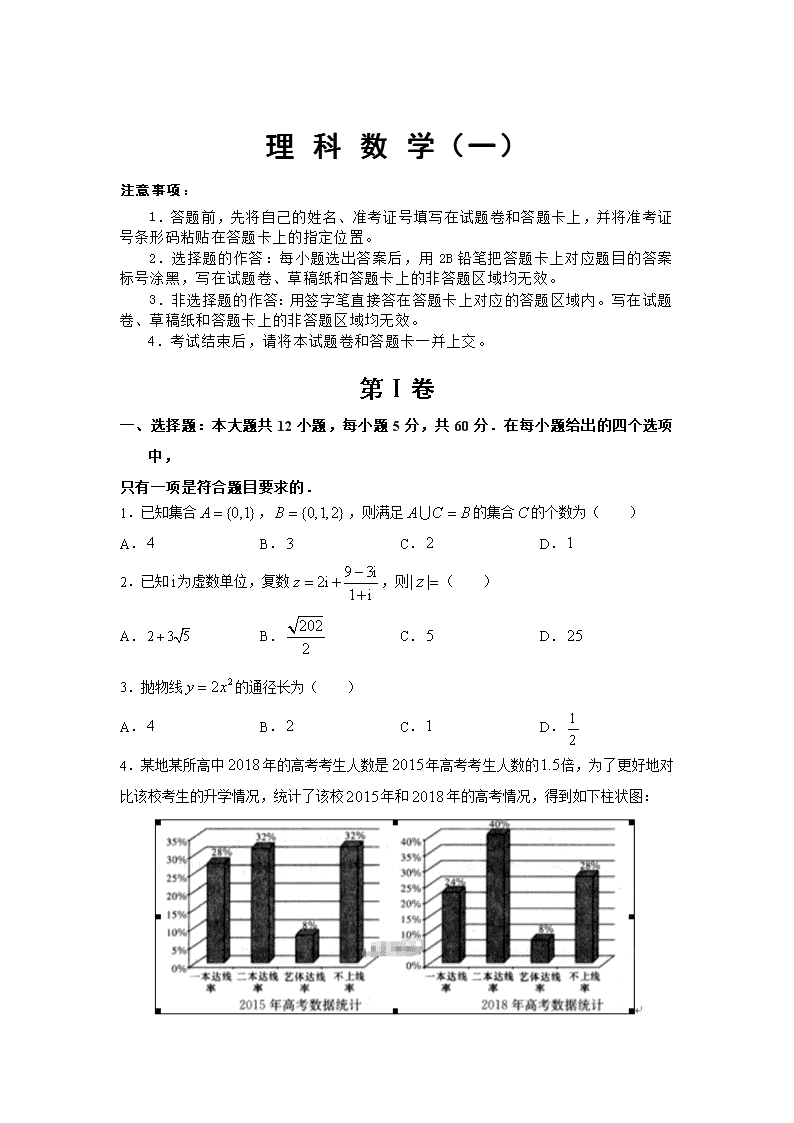
理 科 数 学(一) 注意事项: 1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。 2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。 3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。 4.考试结束后,请将本试题卷和答题卡一并上交。 第Ⅰ卷 一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中, 只有一项是符合题目要求的. 1.已知集合,,则满足的集合的个数为( ) A. B. C. D. 2.已知为虚数单位,复数,则( ) A. B. C. D. 3.抛物线的通径长为( ) A. B. C. D. 4.某地某所高中年的高考考生人数是年高考考生人数的倍,为了更好地对比该校考生的升学情况,统计了该校年和年的高考情况,得到如下柱状图: 则下列结论正确的是( ) A.与年相比,年一本达线人数减少 B.与年相比,年二本达线人数增加了倍 C.年与年艺体达线人数相同 D.与年相比,年不上线的人数有所增加 5.我国古代的《洛书》中记载着世界上最古老的一个幻方:如图,将填入的方格内,使三行,三列和两条对角线上的三个数字之和都等于.一般地,将连续的正整数填入个方格中,使得每行,每列和两条对角线上的数字之和都相等,这个正方形叫做阶幻方记阶幻方的对角线上的数字之和为,如图三阶幻方的,那么的值为( ) A. B. C. D. 6.根据如下样本数据 得到的回归方程为,则( ) A., B., C., D., 7.设是任意等比数列,它的前项和,前项和与前项和分别为,,,则下列等式中恒成立的是( ) A. B. C. D. 8.设,,,则,,的大小关系是( ) A. B. C. D. 9.已知函数的最小正周期是,将函数的 图象向左平移个单位长度后所得的函数图象过点,则下列结论中正确的是( ) A.的最大值为 B.在区间上单调递增 C.的图像关于直线对称 D.的图像关于点对称 10.过正方体的顶点作平面,使得正方体的各棱与平面所成的角都相等,则满足条件的平面的个数为( ) A. B. C. D. 11.椭圆与双曲线共焦点,,它们在第一象限的交点为,设,椭圆与双曲线的离心率分别为,,则( ) A. B. C. D. 12.已知正方形的边长为,为内一点,满足, 则( ) A. B. C. D. 第Ⅱ卷 二、填空题:本大题共4小题,每小题5分,共20分. 13.展开式中的系数为 . 14.设实数,满足不等式,当时取得最小值时,直线与以为圆心的圆相切,则圆的面积为 . 15.已知等差数列的公差,,则使得集合, 恰好有两个元素的的值为 . 16.在三棱锥中,,,,若与底面 所成的角为,则点到底面的距离是 ;三棱锥的外接球的表面积是 . 三、解答题:本大题共6个大题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(12分)已知、分别在射线、(不含端点)上运动,,在中,角、、所对的边分别是,,. (1)若,,依次成等差数列,且公差为,求的值; (2)若,,试用表示的周长,并求周长的最大值. 18.(12分)如图,在三棱锥中,底面是边长为的正三角形,,底面,点,分别为,的中点. (1)求证:平面平面; (2)在线段上是否存在点,使得直线与平面所成的角的正弦值为?若存在,确定点的位置;若不存在,请说明理由. 19.(12分)已知,,,. (1)求的轨迹; (2)过轨迹上任意一点作圆的切线,,设直线,,的斜率分别是,,,试问在三个斜率都存在且不为的条件下,时候是定值,请说明理由,并加以证明. 20.(12分)已知函数. (1)求函数的单调区间; (2)若对任意的,不等式恒成立,求实数的取值范围. 21.(12分)年月日,国务院总理李克强在做政府工作报告时说,打好精准脱贫攻坚战.江西省贫困县脱贫摘帽取得突破性进展:年,稳定实现扶贫对象“两不愁、三保障”,贫困县全部退出.围绕这个目标,江西正着力加快增收步伐,提高救助水平,改善生活条件,打好产业扶贫、保障扶贫、安居扶贫三场攻坚战.为响应国家政策,老张自力更生开了一间小型杂货店.据长期统计分析,老张的杂货店中某货物每天的需求量在与之间,日需求量(件)的频率分布如下表所示: 己知其成本为每件元,售价为每件元若供大于求,则每件需降价处理,处理价每件元. (1)设每天的进货量为,视日需求量的频率为概率,求在每天进货量为 的条件下,日销售量的期望值(用表示); (2)在(1)的条件下,写出和的关系式,并判断为何值时,日利润的均值最大. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.(10分)【选修4-4:坐标系与参数方程】 在直角坐标系中,直线的参数方程为(为参数),在以坐标原点为极点, 轴正半轴为极轴的极坐标系中,曲线. (1)求直线的普通方程和曲线的直角坐标方程; (2)求曲线上的点到直线的距离的最大值. 23.(10分)【选修4-5:不等式选讲】 设,,且. (1)若不等式恒成立,求实数的取值范围; (2)是否存在实数,,使得?并说明理由 理 科 数 学(一)答 案 第Ⅰ卷 一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中, 只有一项是符合题目要求的. 1.【答案】A 【解析】由可知集合中一定有元素, 所以符合要求的集合有,,,共种情况. 2.【答案】C 【解析】对复数进行化简:, 所以. 3.【答案】D 【解析】标准化,通径. 4.【答案】D 【解析】设年该校参加高考的人数为,则年该校参加高考的人数为. 对于选项A,年一本达线人数为,年一本达线人数为, 可见一本达线人数增加了,故选项A错误; 对于选项B,年二本达线人数为,年二本达线人数为, 显然年二本达线人数不是增加了倍,故选项B错误; 对于选项C,年和年,艺体达线率没变,但是人数是不相同的,故选项C错误; 对于选项D,年不上线人数为,年不上线人数为, 不达线人数有所增加. 5.【答案】A 【解析】根据题意可知,幻方对角线上的数成等差数列,, ,, …, ∴, ∴. 6.【答案】A 【解析】画出散点图知,,故选A. 7.【答案】D 【解析】由等比数列的性质得,,成等比数列,,化简得. 8.【答案】C 【解析】, ,. 9.【答案】B 【解析】由条件知,结合图像得B. 10.【答案】C 【解析】在正方体中,四面体的四面与条棱所成的角相等, ∴正方体的条棱所在的直线所成的角均相等的平面有个. 11.【答案】B 【解析】设椭圆的长轴长为,双曲线的实轴长为, 交点到两焦点的距离分别为,焦距为, 则, 又,,故,,. 12.【答案】D 【解析】设正方形的边长为, 在中,由正弦定理得, 在中,由余弦定理得, ∴为等腰三角形,. 第Ⅱ卷 二、填空题:本大题共4小题,每小题5分,共20分. 13.【答案】 【解析】展开式中含的项为, 即的系数为. 14.【答案】 【解析】当直线过点时,取得最小值, 故,从而圆的面积为. 15.【答案】 【解析】要使得集合恰好有两个元素,可以使,的终边关于轴对称,此时. 16.【答案】; 【解析】将三棱锥置于长方体中,其中平面, 由与底面所成的角为,可得,即为点到底面的距离, 由,得, 如图,就是长方体(三条棱长分别为,,)外接球的直径, 也是三棱锥外接球的直径,即, 所以球的表面积为. 三、解答题:本大题共6个大题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.【答案】(1);(2)周长,时,取得最大值为. 【解析】(1),,成等差数列,且公差为,∴,, 又,,∴, 恒等变形得,解得或, 又∵,∴. (2)在中,, ∴,,, ∴的周长 , 又∵,∴, 当,即时,取得最大值. 18.【答案】(1)证明见解析;(2)存在,为线段的中点. 【解析】(1)证明:∵,为的中点,∴, 又平面,平面,∴, ∵,∴平面, ∵平面,∴平面平面. (2)如图,由(1)知,,,点,分别为,的中点, ∴,∴,, 又,∴,,两两垂直, 分别以,,方向为,,轴建立坐标系, 则,,,, 设,, 所以,,, 设平面的法向量为,则, 令,则,,∴, 由已知或(舍去), 故,故线段上存在点, 使得直线与平面所成的角的正弦值为,此时为线段的中点. 19.【答案】(1);(2)为定值,详见解析. 【解析】(1)方法一:如图因为,所以四边形是平行四边形, 所以, 由,得, 所以的轨迹以,为焦点的椭圆易知,, 所以方程为. 方法二:设,由,得, 再,得, 移项,平方化简得. (从发现是椭圆方程也可以直接得,). (2)设,过的斜率为的直线为, 由直线与圆相切可得,即, 由已知可得,是方程(关于)的两个根, 所以由韦达定理:,两式相除, 又因为,所以, 代入上式可得,即为定值. 20.【答案】(1)见解析;(2). 【解析】(1),记, 令,得,函数在上单调递增;,得或,函数在或上单调递减. (2)记, 由,,得或, ∵,所以. ①当时,,且时,; 时,, 所以, ∴时,恒成立; ②当时,, 因为,所以,此时单调递增, 且,所以,成立; ③当时,,, 所以存在使得,因此不恒成立, 综上,的取值范围是. 21.【答案】(1)见解析;(2)件. 【解析】(1)当日需求量时,日销售量为; 日需求量时,日销售量为, 故日销售量的期望为: 当时,; 当时,. (2), 设每天进货量为,日利润为, 则,, 由, 又∵,, ∴最大,所以应进货件时,日利润均值最大. 22.【答案】(1),;(2). 【解析】(1)由,消去,得, 所以直线的普通方程为, 由, 得, 将,,代入上式, 得曲线的直角坐标方程为,即. (2)设曲线上的点为, 则点到直线的距离 , 当时,, 所以曲线上的点到直线的距离的最大值为. 23.【答案】(1);(2)不存在,详见解析. 【解析】(1)由,得,, 当且仅当时成立. 不等式,即为, 当时,不等式为,此时; 当时,不等式成立,此时; 当时,不等式为,此时, 综上,实数的取值范围是. (2)由于,, 则, 当且仅当,即,时,取得最小值, 所以不存在实数,,使得成立查看更多