- 2021-04-22 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年河南省郸城县第一高级中学高二11月月考数学试题(解析版)
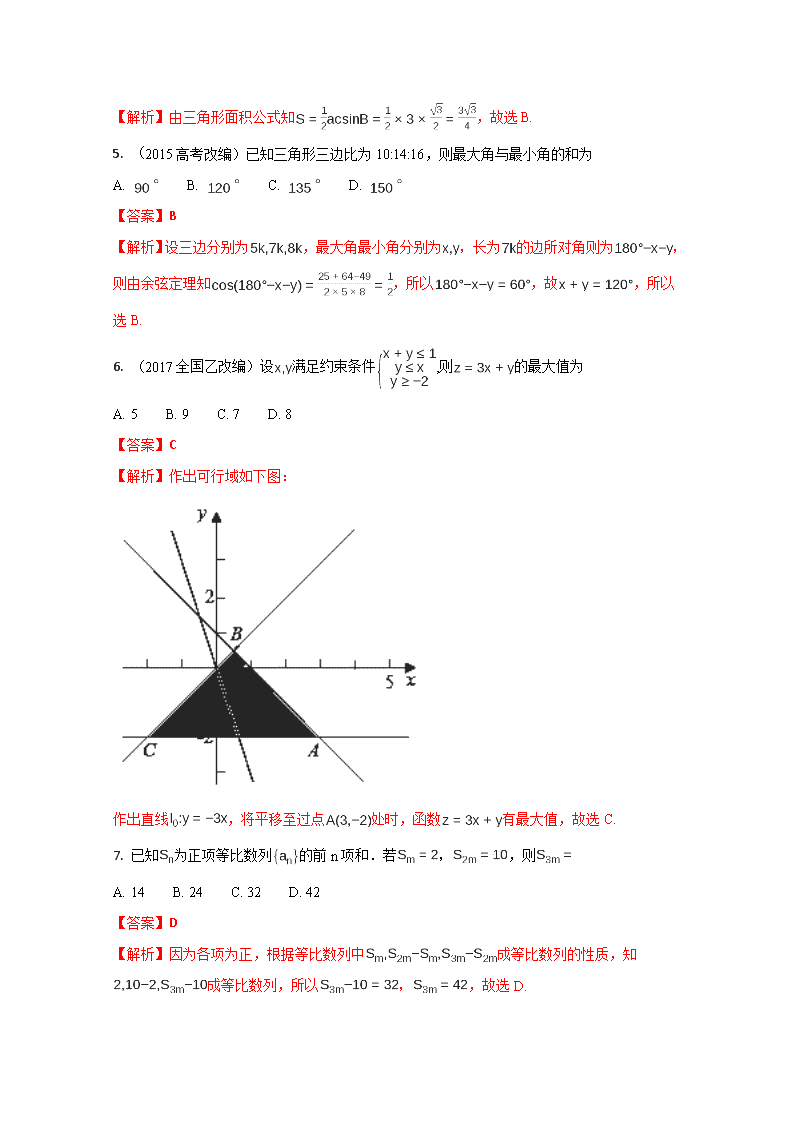
2017-2018学年河南省郸城县第一高级中学高二11月月考数学试题(解析版) 第Ⅰ卷 一、选择题:本大题共12小题,每小题5分,共60分. 每小题给出的四个选项中只有一项是符合要求的. 1. 已知数列 则是它的 A. 第30项 B. 第31项 C. 第32项 D. 第33项 【答案】C 【解析】根据所给数列的项,可以得到其通项,故,解得,故选C. 2. 已知,函数的最小值是 A. 4 B. 5 C. 6 D. 8 【答案】D 【解析】当时,,当且仅当,即时,等号成立,故选D. 3. (2016全国1改编)记为等差数列的前n项和.若,则 A. 72 B. 48 C. 64 D. 54 【答案】A 【解析】根据等差数列的性质可知,所以,故选A. .................. 4. 中,若,则的面积为 A. B. C. D. 【答案】B 【解析】由三角形面积公式知,故选B. 5. (2015高考改编)已知三角形三边比为10:14:16,则最大角与最小角的和为 A. B. C. D. 【答案】B 【解析】设三边分别为,最大角最小角分别为,长为的边所对角则为,则由余弦定理知,所以,故,所以选B. 6. (2017全国乙改编)设满足约束条件,则的最大值为 A. 5 B. 9 C. 7 D. 8 【答案】C 【解析】作出可行域如下图: 作出直线,将平移至过点处时,函数有最大值,故选C. 7. 已知为正项等比数列的前n项和.若,,则 A. 14 B. 24 C. 32 D. 42 【答案】D 【解析】因为各项为正,根据等比数列中成等比数列的性质,知成等比数列,所以,,故选D. 8. 数列的最大项为第项,则= A. 4或5 B. 5 C. 5或6 D. 6 【答案】C 【解析】∵数列的最大项为第项, ∴即, 由于是正整数,所以或,故选C. 9. 设数列满足,且,则 A. B. C. D. 【答案】C ,故选C. 10. (2015高考改编)已知为正项等比数列,为等差数列,且,则下列关系式必成立的是 A. B. C. D. 【答案】A 【解析】∵ ,而, 即,故选A. 11. (2013陕西改编)在如图所示的锐角三角形空地中,欲建一个面积不小于400m2的内接矩形花园(阴影部分),则其边长(单位:m )的取值范围是 A. B. C. D. 【答案】C 【解析】设矩形的另一边长为m,由相似三角形的性质可得:,解得,∴矩形的面积, ∵矩形花园的面积不小于400m2, ∴,化为,解得.满足.故其边长x(单位m)的取值范围是.故答案为. 12. (2013山东改编)设正实数满足, 则当取得最大值时,的最大值为 A. 1 B. 4 C. D. 【答案】B 【解析】∵ ,∴ ∴ ,当且仅当时取等号, ∴ 当取最大值时, ∴ ∴当时,有最大值,故选B. 点睛:本题是均值不等式的灵活运用问题,属于难题。解决此类问题,需要观察条件和结论,结合二者构造新的式子,对待求式子进行变形,方能形成使用均值不等式的条件,本题注意到,所以使用了重要不等式,从而解决问题。 第Ⅱ卷 二、填空题:本题共4小题,每小题5分,共20分. 13. 在等比数列中,若,,则__________. 【答案】或; 【解析】∵,∴ ,又 ∴或, ∴ 或 ∴ 或.故填或. 14. 在中,面积为,则________. 【答案】; 【解析】试题分析:由三角形面积公式得,解得.再由余弦定理得,解得.由正弦定理及合比性质得, 考点:三角形面积公式正弦定理、余弦定理的应用合比性质 15. (2016年江苏改编)已知实数满足,则的取值范围是_______. 【答案】; 【解析】作出可行域如图: 的几何意义为,可行域内一点与定点的距离的平方,因此过分别向三条直线做垂线段,,,,故最小值为,连接三个顶点,计算知最大值为5,故取值范围. 点睛:本题考查线性规划问题,涉及到非线性目标函数中问题,综合性要求较高,属于难题.解决此类问题时,首先做出可行域,然后结合目标函数的几何意义进行分类讨论,本题几何意义为点到点的距离的平方的最大值和最小值,一般最小值是通过点向边界做垂线段,而最大值一般为点与可行域顶点的距离,分别求出比较大小,即可得到最大值与最小值. 16. (2016安徽模拟改编)已知数列的前n项和为, ,若 对任意的恒成立,则实数的取值范围是_______. 【答案】 【解析】由得 ; 当时,, 为偶数时,则,∴ (n为正奇数); 为奇数时,,∴ (n为正偶数); 函数(n为正奇数)是减函数,有最大值.函数(n为正偶数)是增函数,最大值,综上,,故只需,填. 点睛:本题考查了与的关系,以及分类讨论的思想,以及数列中求最值、恒成立等问题,属于难题.解决数列的最值时,一般要根据数列的单调性进行处理,本题特别是对项数进行了奇偶分类,要分别研究奇数项和偶数项的最大值,从而利用恒成立求出参数的取值范围,由求也是本题的一个难点,一定要注意分析全面严谨. 三、解答题:本大题共6小题,共70分,解答应写出文字、证明过程或演算步骤. 17. 已知圆内接四边形ABCD的边 (Ⅰ)求角C的大小和BD的长; (Ⅱ)求四边形ABCD的面积及外接圆的半径. 【答案】(Ⅰ) ; (Ⅱ) 面积; 外接圆半径为 【解析】试题分析:(1)连结BD,由于A+C=180°,则,在中,和在中分别应用余弦定理即可求得BD和角C; (2)由于A+C=180°,则sinA=sinC,由四边形ABCD的面积为S△ABD+S△BCD,应用面积公式可得面积,再由正弦定理,得到边与角的比值,即为外接圆的半径. 试题解析: (1)如图,连结BD,由于,所以。 由题设及余弦定理得 在中,① 在中,② 由①②得=, 解得, 又, 故 则。 (2) 因为,所以。 ∴四边形ABCD的面积 。 由正弦定理可得四边形ABCD的外接圆半径。 点睛:解三角形在平面几何中的应用是常见题型,解题时首先要把问题转化在三角形中,并明确给出的条件是角还是边、所求的问题是角还是边,然后确定是用正弦定理还是用余弦定理,解题中一定要注意平面几何知识在解题中的应用。 18. (2016广东模拟改编)记为等差数列的前项和,已知, . (Ⅰ)求的通项公式; (Ⅱ)令, ,若对一切成立,求实数的最大值. 【答案】(Ⅰ) ; (Ⅱ) 实数的最大值为2 【解析】试题分析:(1)根据等差数列的通项公式,前n项和公式,列方程组求解即可;(2)采用裂项相消的方法求和,分析单调性即可求参数的范围. 试题解析:(1)∵等差数列中,,, ∴解得 ∴ , ∴(). (2)∵, ∴, ∵随着增大而增大, ∴是递增数列,又,∴, ∴,∴实数的最小值为5. 点睛:本题考查了等差数列中基本量的计算,体现了方程思想,以及数列求和的方法,属于中档题.数列求和的方法主要有错位相减法、裂项相消法,公式法、分组求和等方法,注意根据数列特点选择合适的求和方法,求和后分离参数求出m的取值范围. 19. 在中,角A,B,C的对边分别为a,b,c,已知 ,且a,b,c成等比数列. (Ⅰ)求 的值; (Ⅱ)若求 及的值. 【答案】(Ⅰ) ; (Ⅱ) 【解析】试题分析:(1)根据正弦定理与等比数列的定义,得到,然后利用三角恒等变换计算出 的值;(2)利用正弦、余弦定理求出三角形的面积及a+c的值。 试题解析:(Ⅰ)∵成等比数列,∴, 由正弦定理得。 ∴ 。 (Ⅱ) 由得, 又,所以。 ∴。 ∴。 由余弦定理得 , ∴, ∴, ∴。 20. (2015浙江改编)已知为数列前项和, . (Ⅰ)求和(); (Ⅱ)若,求的值. 【答案】(Ⅰ) , ();(Ⅱ) 【解析】试题分析:(Ⅰ)根据已知条件,令,代入化简即可;(Ⅱ)利用数列的周期性,写出结合即可求解. 试题解析:(Ⅰ)解:由已知:() , 所以,(), 又, 所以,. (Ⅱ)又由已知:, 得:, ,得:. 所以,, 解得:,,∴. 21. (2017江西模拟改编)已知数列的前项和为, , .等差数列中, ,且公差. (Ⅰ)求数列的通项公式; (Ⅱ)是否存在正整数,使得?.若存在,求出的最小值;若不存在,请说明理由. 【答案】(Ⅰ) ; ;(Ⅱ)的最小正整数为 【解析】试题分析:(Ⅰ)由可得, 两式相减得,,数列是以为首项,为公比的等比数列,从而可得数列的通项公式,利用等差数列的定义可得的通项公式;(Ⅱ)根据(Ⅰ)求出,利用错位相减法可得数列的前项和,解不等式即可得结果. 试题解析:(Ⅰ),当时,两式相减得,,又,数列是以为首项,为公比的等比数列,,又,. (Ⅱ),令 ① 则 ② ①-②得:,,即,,的最小正整数为. 【易错点晴】本题主要考查等比数列与等差数列的通项、“错位相减法”求数列的和,属于难题. “错位相减法”求数列的和是重点也是难点,利用“错位相减法”求数列的和应注意以下几点:①掌握运用“错位相减法”求数列的和的条件(一个等差数列与一个等比数列的积);②相减时注意最后一项 的符号;③求和时注意项数别出错;④最后结果一定不能忘记等式两边同时除以. 22. 如果函数在区间上单调递减,求mn的最大值. 【答案】最大值为18 【解析】试题分析:首先要分类讨论,当时,根据递减求出范围,当时,根据二次函数的对称轴分析即可求出关于的关系,结合均值不等式即可求出. 试题解析:当时,函数若在区间上单调递减,则,. 当时,抛物线的对称轴为.据题意, (ⅰ)若,抛物线开口向上,函数若在区间上单调递减,只需: 即. ,∴, 当且仅当即时.等号成立. (ⅱ)时,抛物线开口向下,据题意得,即.由且得,故应舍去. 要使得取得最大值,应有 . 所以, 综上所述,最大值为18. 点睛:本题考查了二次函数单调性,以及均值不等式,分类讨论等。属于难题.首先通过分类确定函数的类型,当函数为一次函数时,通过斜率确定增减性,当函数为二次函数时,利用对称轴与区间的关系确定增减性,求积的最值时,注意构造和是定值才能使用均值不等式,并要注意等号是否成立. 查看更多