- 2021-04-22 发布 |
- 37.5 KB |
- 18页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级下数学课件:18-2-1 矩形 (共18张PPT)_人教新课标
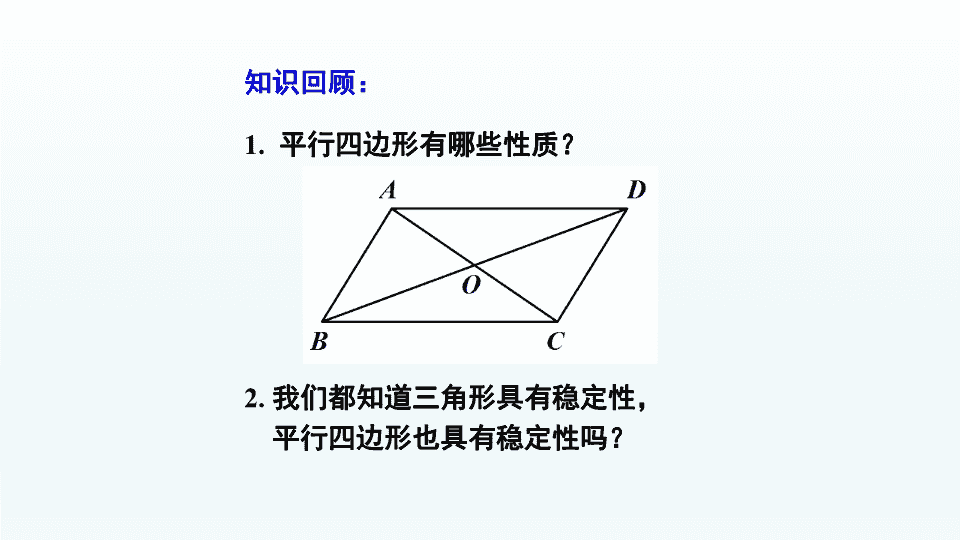
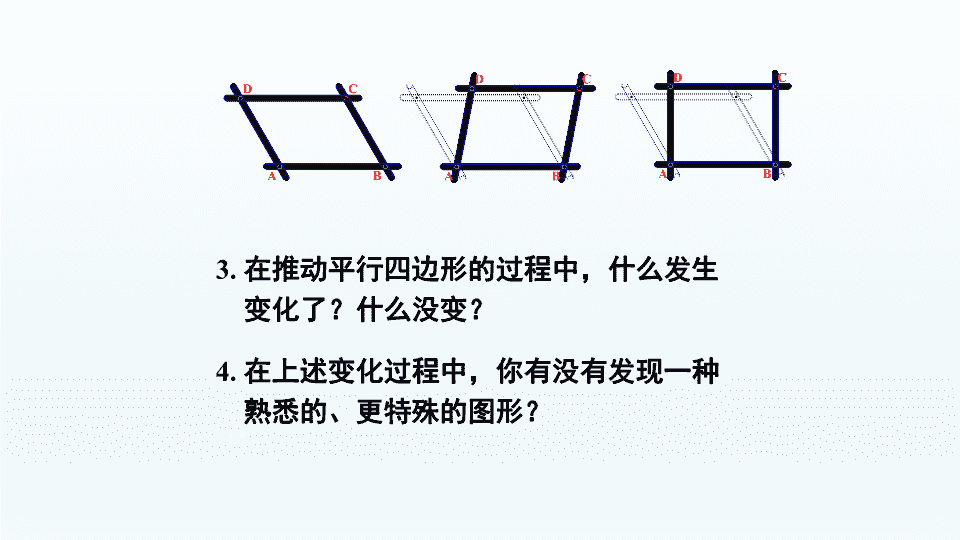
第十八章 平行四边形 知识回顾: 1. 平行四边形有哪些性质? 2. 我们都知道三角形具有稳定性, 平行四边形也具有稳定性吗? 3. 在推动平行四边形的过程中,什么发生 变化了?什么没变? 4. 在上述变化过程中,你有没有发现一种 熟悉的、更特殊的图形? Z```x``xk D C A B A B C D 定义:有一个角是直角的平行四边形叫做矩形. 四边形 平行四边形 矩形 D C A B A B C D 小学里学过的长方形、正方形都是矩形 想一想: 你能举出在人们的日常生活和生产实 践中,有哪些东西是矩形的? 探究新知 活动1、在一个平行四边形活动框架上,用两根橡皮 筋分别套在相对的两个顶点上(作出对角线),拉 动一对不相邻的顶点,改变平行四边形的形状. ① 随着∠α的变化,两条对角线的长度分别是怎样 变化的? ② 当∠α是直角时,平行四边形变成矩形,此时它 的其他内角是什么样的角?它的两条对角线的长度 有什么关系? 请同学们观察、猜测、动手测量验证总结矩形的性 质,并思考如何证明。 活动2、请同学们拿出准备好的两张纸片跟着老师折 叠、旋转探究矩形的对称性? 矩形具有的性质: 1. 矩形具有平行四边形的所有性质. 2. 矩形特有的性质: ① 矩形的四个角都是直角; ② 矩形的对角线相等. 3. 矩形的对称性:是中心对称图形,也是轴对称图形. 活动3:如图,在矩形ABCD中, AC、BD相 交于点O,你在矩形ABCD中还发现了哪些 基本图形? A B C D O A B C D O ◆ 两对全等的等腰三角形. A B C D O ◆ 四个全等的直角三角形. 你在矩形中还发现了哪些基本图形? ◆ 两对全等的等腰三角形. ````zx``xk ◆ 四个全等的直角三角形. A B C D O 例 如图,矩形ABCD的两条对角线 AC,BD相交于点O,∠AOB=60°, AB=4cm. 求矩形对角线的长. 1、自我检测 请你来判断:1.有一个角是直角的四边形是矩形。( ) 2.矩形的对角线互相平分。( ) 细心选一选:3.矩形具有而平行四边形不具有的性质是 ( ) A 两组对边分别平行 B 对角相等 C 对角线互相平分 D 对角线相等 4.下列性质中,矩形不一定具有的是( ) A、对角线相等 B、 四个角都相等 C、对角线垂直 D、是轴对称图形 2、拓展练习 已知:如图 ,矩形 ABCD,AB长8 cm , 对角线比AD边长4 cm.求AD的长及点 A到BD的距离AE的长. 课堂练习 课堂小结: 1.用几何图形展示四边形、平行四边形、矩形的 从属关系,让学生看了一目了然。 2.引导学生从角、对角线、对称性等方面总结归 纳矩形的性质 ,有助于学生对矩形性质的记忆。 平行四边形 矩形 边 角 对角线 对边平行且相等 对角相等 对角线互相平分 对角线相等且 互相平分 四个角都是直角 对边平行且相等 矩形的问题经常转化到等腰三角形或 直角三角形中解决. 布置作业: 教材P53练习第1、2、3题. 矩形之歌 脸蛋方方是矩形,例如课本和门窗。 对角线段皆相等,相互交叉且平分。 内有直角三角形,斜边中线半斜边。 若要牢记其定义,直角平行四边形。查看更多