2018年四川省遂宁市高考数学一诊试卷（文科）

2018年四川省遂宁市高考数学一诊试卷（文科）

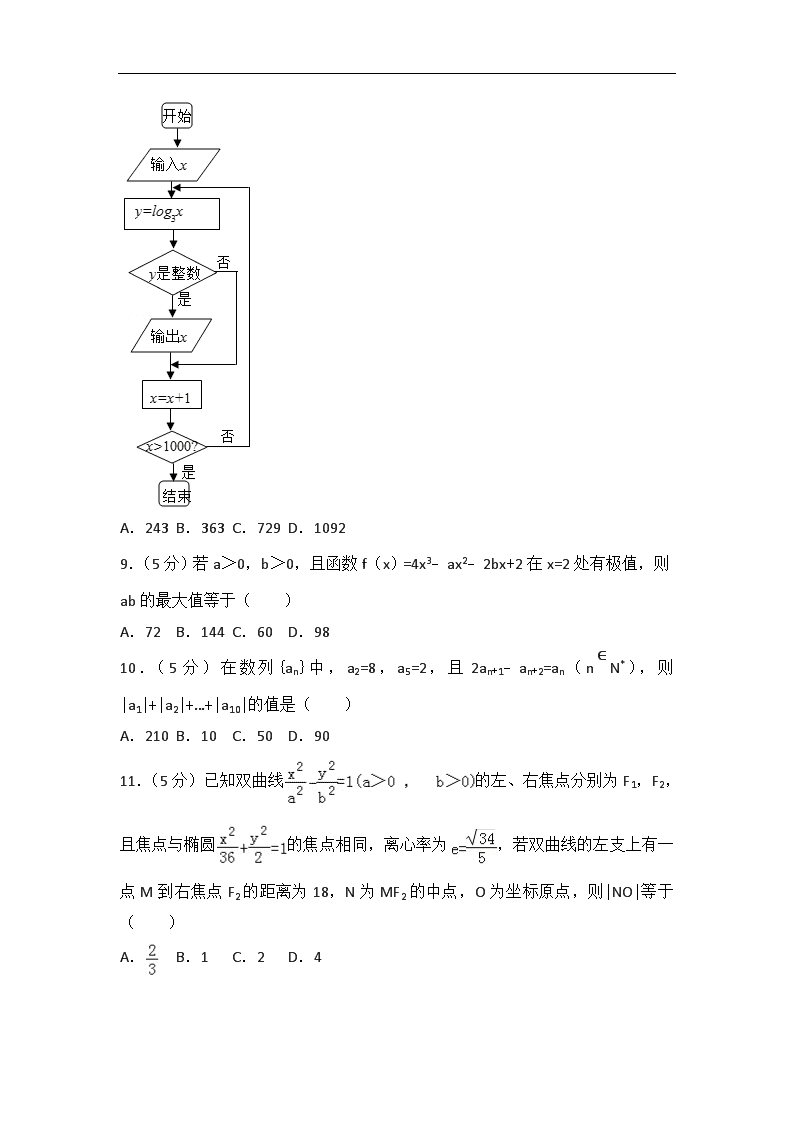
‎2018年四川省遂宁市高考数学一诊试卷（文科）‎ ‎　‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一个是符合题目要求的．‎ ‎1．（5分）已知集合A={x|﹣3＜x＜6}，B={x|2＜x＜7}，则A∩（∁RB）=（　　）‎ A．（2，6） B．（2，7） C．（﹣3，2] D．（﹣3，2）‎ ‎2．（5分）已知复数z=a+i（a∈R），若z+=4，则复数z的共轭复数=（　　）‎ A．2+i B．2﹣i C．﹣2+i D．﹣2﹣i ‎3．（5分）已知α满足cos2α=，则cos（+α）cos（﹣α）=（　　）‎ A． B． C．﹣ D．﹣‎ ‎4．（5分）已知命题p：“a＞b”是“2a＞2b”的充要条件；q：∃x∈R，ex＜lnx，则（　　）‎ A．￢p∨q为真命题 B．p∧￢q为假命题 C．p∧q为真命题 D．p∨q为真命题 ‎5．（5分）向量=（2，﹣1），=（﹣1，2），则（2+）•=（　　）‎ A．1 B．﹣1 C．﹣6 D．6‎ ‎6．（5分）设x，y满足约束条件，则目标函数z=2x+y的最小值是（　　）‎ A．﹣15 B．﹣9 C．1 D．9‎ ‎7．（5分）已知x1，x2（x1＜x2）是函数f（x）=﹣lnx的两个零点，若a∈（x1，1），b∈（1，x2），则（　　）‎ A．f（a）＜0，f（b）＜0 B．f（a）＜0，f（b）＞0 C．f（a）＞0，f（b）＞0 D．f（a）＞0，f（b）＜0‎ ‎8．（5分）执行如图所示的程序，若输入的x=3，则输出的所有x的值的和为（　　）‎ A．243 B．363 C．729 D．1092‎ ‎9．（5分）若a＞0，b＞0，且函数f（x）=4x3﹣ax2﹣2bx+2在x=2处有极值，则ab的最大值等于（　　）‎ A．72 B．144 C．60 D．98‎ ‎10．（5分）在数列{an}中，a2=8，a5=2，且2an+1﹣an+2=an（n∈N*），则|a1|+|a2|+…+|a10|的值是（　　）‎ A．210 B．10 C．50 D．90‎ ‎11．（5分）已知双曲线的左、右焦点分别为F1，F2，且焦点与椭圆的焦点相同，离心率为，若双曲线的左支上有一点M到右焦点F2的距离为18，N为MF2的中点，O为坐标原点，则|NO|等于（　　）‎ A． B．1 C．2 D．4‎ ‎12．（5分）已知函数f（x）=，且有f（x）≤a﹣2恒成立，则实数a的取值范围为（　　）‎ A．[0，2e2] B．[0，2e3] C．（0，2e2] D．（0，2e3]‎ ‎　‎ 二、填空题：本大题共4个小题，每小题5分，共20分．‎ ‎13．（5分）曲线f（x）=x3﹣x+3在点P（1，f（1））处的切线方程为　 　．‎ ‎14．（5分）已知{an}是等比数列，若=（a2，2），=（a3，3），且∥，则=　 　．‎ ‎15．（5分）甲、乙两人参加歌咏比赛的得分（均为两位数）如茎叶图所示，甲的平均数为b，乙的众数为a，且直线ax+by+8=0与以A（1，﹣1）为圆心的圆交于B，C两点，且∠BAC=120°，则圆C的标准方程为　 　．‎ ‎16．（5分）若两曲线y=x2﹣1与y=alnx﹣1存在公切线，则正实数a的取值范围是　 　．‎ ‎　‎ 三、解答题：本大题共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（12分）在各项均不相等的等差数列{an}中，已知a4=5，且a3，a5，a8成等比数列 ‎（1）求an；‎ ‎（2）设数列{an}的前n项和为Sn，记bn=，求数列{bn}的前n项和Tn．‎ ‎18．（12分）已知函数，在△ABC中，角A，B，C的对边分别为a，b，c ‎（1）当x∈[0，]时，求函数f（x）的取值范围；‎ ‎（2）若对任意的x∈R都有f（x）≤f（A），c=2b=4，点D是边BC的中点，求的值．‎ ‎19．（12分）2017年10月18日至10月24日，中国共产党第十九次全国代表大会（简称党的“十九大”）在北京召开．一段时间后，某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查，调查问卷共有20个问题，每个问题5分，调查结束后，发现这100名员工的成绩都在[75，100]内，按成绩分成5组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，绘制成如图所示的频率分布直方图，已知甲、乙、丙分别在第3，4，5组，现在用分层抽样的方法在第3，4，5组共选取6人对“十九大”精神作深入学习．‎ ‎（1）求这100人的平均得分（同一组数据用该区间的中点值作代表）；‎ ‎（2）求第3，4，5组分别选取的作深入学习的人数；‎ ‎（3）若甲、乙、丙都被选取对“十九大”精神作深入学习，之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度，求甲、乙、丙这3人至多有一人被选取的概率．‎ ‎20．（12分）已知点M（x，y）与定点F2（1，0）的距离和它到直线x=4的距离的比是常数 ‎（1）求点M的轨迹方程，并说明轨迹是什么图形；‎ ‎（2）若点F1的坐标为（﹣1，0），过F2‎ 的直线l与点M的轨迹交于不同的两点A，B，求△F1AB面积的最大值．‎ ‎21．（12分）已知函数f（x）=‎ ‎（1）求函数f（x）的单调区间和极值点；‎ ‎（2）当x≥1时，f（x）≤a（1﹣）恒成立，求实数a的取值范围．‎ ‎　‎ 请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]‎ ‎22．（10分）已知直线l的参数方程为（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=4cos（θ﹣）．‎ ‎（1）求圆C的直角坐标方程；‎ ‎（2）若P（x，y）是直线l与圆面的公共点，求x+y的取值范围．‎ ‎23．已知函数f（x）=|1﹣x﹣a|+|2a﹣x|‎ ‎（1）若f（1）＜3，求实数a的取值范围；‎ ‎（2）若a≥，x∈R，判断f（x）与1的大小关系并证明．‎ ‎　‎ ‎2018年四川省遂宁市高考数学一诊试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一个是符合题目要求的．‎ ‎1．（5分）已知集合A={x|﹣3＜x＜6}，B={x|2＜x＜7}，则A∩（∁RB）=（　　）‎ A．（2，6） B．（2，7） C．（﹣3，2] D．（﹣3，2）‎ ‎【解答】解：∵B={x|2＜x＜7}，‎ ‎∴∁RB）={x|x≤2或x≥7}，‎ ‎∴A∩（∁RB）=（﹣3，2]，‎ 故选：C．‎ ‎　‎ ‎2．（5分）已知复数z=a+i（a∈R），若z+=4，则复数z的共轭复数=（　　）‎ A．2+i B．2﹣i C．﹣2+i D．﹣2﹣i ‎【解答】解：∵z=a+i，‎ ‎∴z+=2a=4，得a=2．‎ ‎∴复数z的共轭复数=2﹣i．‎ 故选：B．‎ ‎　‎ ‎3．（5分）已知α满足cos2α=，则cos（+α）cos（﹣α）=（　　）‎ A． B． C．﹣ D．﹣‎ ‎【解答】解：∵α满足cos2α=，则cos（+α）cos（﹣α）=cos（+α）cos[﹣（+α）]‎ ‎=cos（+α）sin（+α）=sin（+2α）=cos2α=，‎ 故选：A．‎ ‎　‎ ‎4．（5分）已知命题p：“a＞b”是“2a＞2b”的充要条件；q：∃x∈R，ex＜lnx，则（　　）‎ A．￢p∨q为真命题 B．p∧￢q为假命题 C．p∧q为真命题 D．p∨q为真命题 ‎【解答】解：命题p：“a＞b”⇔“2a＞2b”，是真命题．‎ q：令f（x）=ex﹣lnx，f′（x）=．x∈（0，1]时，f（x）＞0；x＞1时，f（x）单调递增，∴f（x）＞f（1）=e＞0．‎ ‎∴不存在x∈R，ex＜lnx，是假命题．‎ ‎∴只有p∨q为真命题．‎ 故选：D．‎ ‎　‎ ‎5．（5分）向量=（2，﹣1），=（﹣1，2），则（2+）•=（　　）‎ A．1 B．﹣1 C．﹣6 D．6‎ ‎【解答】解：，；‎ ‎∴．‎ 故选：D．‎ ‎　‎ ‎6．（5分）设x，y满足约束条件，则目标函数z=2x+y的最小值是（　　）‎ A．﹣15 B．﹣9 C．1 D．9‎ ‎【解答】解：x，y满足约束条件的可行域如图：‎ 在坐标系中画出可行域△ABC，A（﹣6，﹣3），B（0，1），C（6，﹣3），‎ 由图可知，当x=﹣6，y=﹣3时，则目标函数z=2x+y的最小，最小值为﹣15．‎ 故选：A．‎ ‎　‎ ‎7．（5分）已知x1，x2（x1＜x2）是函数f（x）=﹣lnx的两个零点，若a∈（x1，1），b∈（1，x2），则（　　）‎ A．f（a）＜0，f（b）＜0 B．f（a）＜0，f（b）＞0 C．f（a）＞0，f（b）＞0 D．f（a）＞0，f（b）＜0‎ ‎【解答】解：令f（x）=0，则lnx=，‎ 分别作出y=lnx和y=的图象，‎ 可得0＜x1＜1，1＜x2，‎ 由a∈（x1，1），b∈（1，x2），‎ 可得lna＞，即f（a）=﹣lna＜0，‎ lnb＜，即f（b）=﹣lnb＞0，‎ 故选：B．‎ ‎　‎ ‎8．（5分）执行如图所示的程序，若输入的x=3，则输出的所有x的值的和为（　　）‎ A．243 B．363 C．729 D．1092‎ ‎【解答】解：模拟程序的运行可得：当x=3时，y是整数；‎ 当x=32时，y是整数；‎ 依此类推可知当x=3n（n∈N*）时，y是整数，‎ 则由x=3n≥1000，得n≥7，‎ 所以输出的所有x的值为3，9，27，81，243，729，其和为1092，‎ 故选：D．‎ ‎　‎ ‎9．（5分）若a＞0，b＞0，且函数f（x）=4x3﹣ax2﹣2bx+2在x=2处有极值，则ab的最大值等于（　　）‎ A．72 B．144 C．60 D．98‎ ‎【解答】解：由题意，求导函数f′（x）=12x2﹣2ax﹣2b，‎ ‎∵在x=2处有极值，‎ ‎2a+b=24，‎ ‎∵a＞0，b＞0‎ ‎∴2ab≤（）2=144，当且仅当2a=b时取等号 所以ab的最大值等于72，‎ 故选：A．‎ ‎　‎ ‎10．（5分）在数列{an}中，a2=8，a5=2，且2an+1﹣an+2=an（n∈N*），则|a1|+|a2|+…+|a10|的值是（　　）‎ A．210 B．10 C．50 D．90‎ ‎【解答】解：∵2an+1﹣an+2=an（n∈N*），即2an+1=an+2+an（n∈N*），‎ ‎∴数列{an}是等差数列，‎ 设公差为d，则a1+d=8，a1+4d=2，‎ 联立解得a1=10，d=﹣2，‎ ‎∴an=10﹣2（n﹣1）=12﹣2n．‎ 令an≥0，解得n≤6．‎ Sn==11n﹣n2．‎ ‎∴|a1|+|a2|+…+|a10|=a1+a2+…+a6﹣a7﹣…﹣a10‎ ‎=2S6﹣S10‎ ‎=2（11×6﹣62）﹣（11×10﹣102）‎ ‎=50．‎ 故选：C．‎ ‎　‎ ‎11．（5分）已知双曲线的左、右焦点分别为F1，F2，且焦点与椭圆的焦点相同，离心率为，若双曲线的左支上有一点M到右焦点F2的距离为18，N为MF2的中点，O为坐标原点，则|NO|等于（　　）‎ A． B．1 C．2 D．4‎ ‎【解答】解：椭圆的焦点 为（±，0），‎ 可得双曲线的c=，‎ 离心率为，可得a=5，‎ 由双曲线左支上有一点M到右焦点F2的距离为18，‎ N是MF2的中点，‎ 连接MF1，‎ ON是△MF1F2的中位线，‎ 可得ON∥MF1，‎ ‎|ON|=|MF1|，‎ 由双曲线的定义知，|MF2|﹣|MF1|=2×5，‎ ‎∴|MF1|=8．‎ ‎∴|ON|=4，‎ 故选：D．‎ ‎　‎ ‎12．（5分）已知函数f（x）=，且有f（x）≤a﹣2恒成立，则实数a的取值范围为（　　）‎ A．[0，2e2] B．[0，2e3] C．（0，2e2] D．（0，2e3]‎ ‎【解答】解：当x＞0时，f（x）=alnx﹣x2﹣2，‎ 若a＜0时，f（x）在（0，+∞）为减函数，此时函数无最大值，即不满足题意，‎ 当a=0时，f（x）≤a﹣2，即为﹣x2﹣2≤a﹣2，即x2≥0恒成立，满足题意，‎ 当a＞0时，f（x）=alnx﹣x2﹣2，f′（x）=﹣2x=，‎ 令f′（x）=0，解得x=，或x=﹣舍去，‎ 当f′（x）＞0，解得0＜x＜，此时函数f（x）单调递增，‎ 当f′（x）＜0，解得x＞，此时函数f（x）单调递减，‎ ‎∴f（x）max=f（）=aln﹣﹣2=ln﹣﹣2，‎ ‎∴ln﹣﹣2≤a﹣2，‎ 即0＜a≤2e3，‎ x＜0时，f（x）=x++a，此时函数f（x）在（﹣∞，﹣1）为减函数，在（0，1）为增函数，‎ ‎∴f（x）max=f（﹣1）=﹣2+a≤a﹣2恒成立，‎ 综上所述a的取值范围为[0，2e3]，‎ 故选：B ‎　‎ 二、填空题：本大题共4个小题，每小题5分，共20分．‎ ‎13．（5分）曲线f（x）=x3﹣x+3在点P（1，f（1））处的切线方程为　2x﹣y+1=0　．‎ ‎【解答】解：根据题意，对于f（x）=x3﹣x+3，其导数f′（x）=3x2﹣1，‎ 当x=1时，f′（1）=3﹣1=2，即切线的斜率k=2，‎ f（1）=1﹣1+3=3，即切点P的坐标为（1，3），‎ 则曲线在点P处的切线方程为y﹣3=2（x﹣1），‎ 变形可得2x﹣y+1=0；‎ 故答案为：2x﹣y+1=0．‎ ‎　‎ ‎14．（5分）已知{an}是等比数列，若=（a2，2），=（a3，3），且∥，则=　　．‎ ‎【解答】解：=（a2，2），=（a3，3），且∥，‎ ‎∴3a2﹣2a3=0，‎ ‎∴=；‎ 又{an}是等比数列，∴q=；‎ ‎∴===．‎ 故答案为：．‎ ‎　‎ ‎15．（5分）甲、乙两人参加歌咏比赛的得分（均为两位数）如茎叶图所示，甲的平均数为b，乙的众数为a，且直线ax+by+8=0与以A（1，﹣1）为圆心的圆交于B，C两点，且∠BAC=120°，则圆C的标准方程为　（x﹣1）2+（y+1）2=　．‎ ‎【解答】解：由题意知，甲的平均数b为：=20，‎ 乙的众数a是：40，‎ ‎∴直线ax+by+8=0，即10x+5y+2=0，‎ A（1，﹣1）到直线的距离为=，‎ ‎∵直线ax+by+8=0与以A（1，﹣1）为圆心的圆交于B，C两点，且∠BAC=120°，‎ ‎∴r=，‎ ‎∴圆C的方程为（x﹣1）2+（y+1）2=，‎ 故答案为：（x﹣1）2+（y+1）2=．‎ ‎　‎ ‎16．（5分）若两曲线y=x2﹣1与y=alnx﹣1存在公切线，则正实数a的取值范围是　（0，2e]　．‎ ‎【解答】解：两曲线y=x2﹣1与y=alnx﹣1存在公切线，‎ y=x2﹣1的导数y′=2x，y=alnx﹣1的导数为y′=，‎ 设y=x2﹣1相切的切点为（n，n2﹣1）与曲线y=alnx﹣1相切的切点为（m，alnm﹣1），‎ y﹣（n2﹣1）=2n（x﹣n），即y=2nx﹣n2﹣1，‎ y﹣（alnm﹣1）=（x﹣m），即：y=‎ ‎∴‎ ‎∴，‎ ‎∵a＞0，‎ ‎∴‎ 即有解即可，‎ 令g（x）=x2（1﹣lnx），‎ y′=2x（1﹣lnx）+=x（1﹣2lnx）=0，可得x=，‎ ‎∴g（x）在（0，）是增函数；（，+∞）是减函数，g（x）的最大值为：g（）=，‎ 又g（0）=0，‎ ‎∴0，∴0＜a≤2e．‎ 故答案为：（0，2e]．‎ ‎　‎ 三、解答题：本大题共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（12分）在各项均不相等的等差数列{an}中，已知a4=5，且a3，a5，a8成等比数列 ‎（1）求an；‎ ‎（2）设数列{an}的前n项和为Sn，记bn=，求数列{bn}的前n项和Tn．‎ ‎【解答】解：（1）∵{an}为等差数列，设公差为d，‎ 由题意得，‎ 解得d=1或d=0（舍），a1=2，‎ ‎∴an=2+（n﹣1）×1=n+1．‎ ‎（2）由（1）知Sn=，‎ ‎∴bn==﹣，‎ ‎∴=‎ 故Tn=．‎ ‎　‎ ‎18．（12分）已知函数，在△ABC中，角A，B，C的对边分别为a，b，c ‎（1）当x∈[0，]时，求函数f（x）的取值范围；‎ ‎（2）若对任意的x∈R都有f（x）≤f（A），c=2b=4，点D是边BC的中点，求的值．‎ ‎【解答】解：（1）当x∈[0，]时，2x﹣∈[﹣，]，‎ sin（2x﹣）∈[﹣，1]，‎ 所以函数的取值范围是[0，3]； ‎ ‎（2）由对任意的x∈R，都有f（x）≤f（A），得 ‎2A﹣=2kπ+，k∈Z，解得A=kπ+，k∈Z，‎ 又∵A∈（0，π）∴，‎ ‎∵‎ ‎=（c2+b2+2bccosA）=（c2+b2+bc）=×（16+4+8）=7，‎ 所以．‎ ‎　‎ ‎19．（12分）2017年10月18日至10月24日，中国共产党第十九次全国代表大会（简称党的“十九大”）在北京召开．一段时间后，某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查，调查问卷共有20个问题，每个问题5分，调查结束后，发现这100名员工的成绩都在[75，100]内，按成绩分成5组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，绘制成如图所示的频率分布直方图，已知甲、乙、丙分别在第3，4，5组，现在用分层抽样的方法在第3，4，5组共选取6人对“十九大”精神作深入学习．‎ ‎（1）求这100人的平均得分（同一组数据用该区间的中点值作代表）；‎ ‎（2）求第3，4，5组分别选取的作深入学习的人数；‎ ‎（3）若甲、乙、丙都被选取对“十九大”精神作深入学习，之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度，求甲、乙、丙这3人至多有一人被选取的概率．‎ ‎【解答】（本小题满分12分）‎ 解：（1）这100人的平均得分为：‎ ‎×‎ ‎=71.5．…（3分）‎ ‎（2）第3组的人数为0.06×5×100=30，‎ 第4组的人数为0.04×5×100=20，‎ 第5组的人数为0.02×5×100=10，故共有60人，‎ ‎∴用分层抽样在这三个组选取的人数分别为：3，2，1． …（7分）‎ ‎（3）记其他人为甲、乙、丙、丁、戊、己，‎ 则所有选取的结果为（甲、乙）、（甲、丙）、（甲、丁）、（甲、戊）、（甲、己）、‎ ‎（乙、丙）、（乙、丁）、（乙、戊）、（乙、己 ‎ ）、（丙、丁）、（丙、戊）、（丙、己）、‎ ‎（丁、戊）、（丁、己 ）、（戊、己）共15种情况，…（9分）‎ 其中甲、乙、丙这3人至多有一人被选取有12种情况，‎ 故甲、乙、丙这3人至多有一人被选取的概率为． …（12分）‎ ‎　‎ ‎20．（12分）已知点M（x，y）与定点F2（1，0）的距离和它到直线x=4的距离的比是常数 ‎（1）求点M的轨迹方程，并说明轨迹是什么图形；‎ ‎（2）若点F1的坐标为（﹣1，0），过F2的直线l与点M的轨迹交于不同的两点A，B，求△F1AB面积的最大值．‎ ‎【解答】解：（1）由题意可有=，‎ 化简可得点M的轨迹方程为+=1． ‎ 其轨迹是焦点在x轴上，长轴长为4，短轴长为2的椭圆．‎ ‎（2）设A（x1，y1），B（x2，y2），‎ ‎∴△F1AB面积S=|F1F2|•|y1﹣y2|，‎ 由题意知，直线l的方程为x=my+1，‎ 由可得（3m2+4）y2+6my﹣9=0，‎ 则y1+y2=，y1y2=，‎ 又因直线l与椭圆C交于不同的两点，故△＞0，‎ 即（6m）2+36（3m2+4）＞0，‎ 则S=|y1﹣y2|==‎ 令，‎ 令，‎ 上是单调递增函数，‎ 即当t≥1时，f（t）在[1，+∞）上单调递增，‎ 因此有，‎ ‎，‎ 故当t=1，即m=0，三角形的面积最大，最大值为3．‎ ‎　‎ ‎21．（12分）已知函数f（x）=‎ ‎（1）求函数f（x）的单调区间和极值点；‎ ‎（2）当x≥1时，f（x）≤a（1﹣）恒成立，求实数a的取值范围．‎ ‎【解答】解：（1）因为f（x）=，求导得f′（x）=，‎ 令f'（x）=0，解得x=e，…（2分）‎ 又函数的定义域为（0，+∞），当x∈（0，e）时，f'（x）＞0；当x∈（e，+∞）时，f'（x）＜0，‎ 所以函数f（x）在（0，e）单调递增；在（e，+∞）单调递减，‎ 有极大值点x=e；无极小值点． …（4分）‎ ‎（2）由f（x）≤a（1﹣）恒成立，得≤a（1﹣），（x≥1）恒成立，‎ 即xlnx≤a（x2﹣1）（x≥1）恒成立．令g（x）=xlnx﹣a（x2﹣1）（x≥1）‎ g′（x）=lnx+1﹣2ax，令F（　　）=lnx+1﹣2ax，则F′（x）=，…（5分）‎ ‎①若a≤0，F′（x）＞0，g′（x）在[1，+∞）递增，g′（x）≥g′（1）=1﹣2a＞0，‎ 故有g（x）≥g（1）=0不符合题意．…（7分）‎ ‎②若，∴，‎ 从而在上，g′（x）＞g′（1）=1﹣2a＞0，同（1），不合题意…（9分）‎ ‎③若a≥，F′（x）≤0在[1，+∞）恒成立，‎ ‎∴g′（x）在[1，+∞）递减，g′（x）≤g′（1）=1﹣2a≤0，‎ 从而g（x）在[1，+∞）递减，故g（x）≤g（1）=0 …（11分）‎ 综上所述，a的取值范围是[，+∞）．…（12分）‎ ‎　‎ 请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]‎ ‎22．（10分）已知直线l的参数方程为（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=4cos（θ﹣）．‎ ‎（1）求圆C的直角坐标方程；‎ ‎（2）若P（x，y）是直线l与圆面的公共点，求x+y的取值范围．‎ ‎【解答】（本小题满分10分）‎ 解：（1）∵圆C的极坐标方程为ρ=4cos（θ﹣），‎ ‎∴，‎ 又∵ρ2=x2+y2，x=ρcosθ，y=ρsinθ，…（5分）‎ ‎∴，‎ ‎∴圆C的普通方程为=0．‎ ‎（2）设z=，‎ 圆C的方程=0．即（x+1）2+（y﹣）2=4，‎ ‎∴圆C的圆心是C（﹣1，），半径r=2，‎ 将直线l的参数方程为（t为参数）代入z=，得z=﹣t，‎ 又∵直线l过C（﹣1，），圆C的半径是2，‎ ‎∴﹣2≤t≤2，∴﹣2≤﹣t≤2，即的取值范围是[﹣2，2]．…（10分）‎ ‎　‎ ‎23．已知函数f（x）=|1﹣x﹣a|+|2a﹣x|‎ ‎（1）若f（1）＜3，求实数a的取值范围；‎ ‎（2）若a≥，x∈R，判断f（x）与1的大小关系并证明．‎ ‎【解答】解：（1）因为f（1）＜3，所以|a|+|1﹣2a|＜3，‎ ‎①当a≤0时，得﹣a+（1﹣2a）＜3，解得：a＞﹣，所以﹣＜a≤0；‎ ‎②当0＜a＜时，得a+（1﹣2a）＜3，解得a＞﹣2，所以0＜a＜；‎ ‎③当a≥时，得a﹣（1﹣2a）＜3，解得：a＜，‎ 所以≤a＜；‎ 综上所述，实数a的取值范围是（﹣，）．…（5分）‎ ‎（2）f（x）≥1，因为a≥，‎ 所以f（x）=|1﹣x﹣a|+|2a﹣x|≥|（1﹣x﹣a）﹣（2a﹣x）|=|1﹣3a|=3a﹣1≥1…（10分）‎ ‎　‎