2018届二轮复习　功能关系在电学中的应用课件（共34张）（全国通用）

2018届二轮复习　功能关系在电学中的应用课件（共34张）（全国通用）

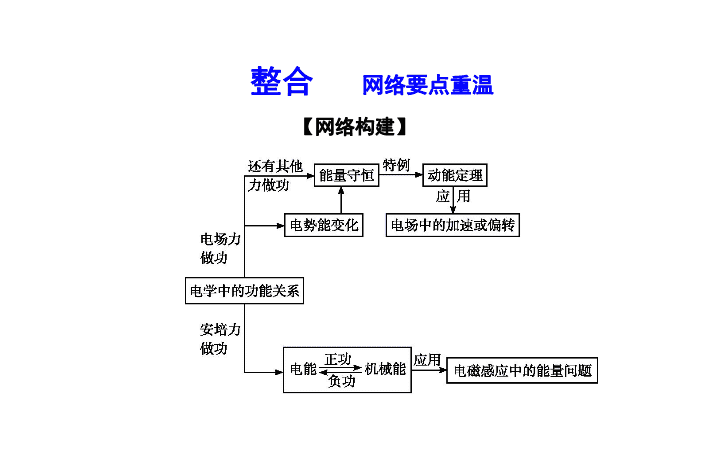
第 2 讲　功能关系在电学中的应用 整 合 突 破 实 战 整合 网络要点重温 【 网络构建 】 【 要点重温 】 1.电场中的功能关系 (1)电场力做功的求法 ①W=qElcos α. ②W= . ③W 电场力 +W 其他力 =ΔE k . (2)电场中的功能关系 ①若只有电场力做功, 与动能之和保持不变. ②若只有电场力和重力做功,电势能、 、动能之和保持不变. 2. - x图线的斜率表示沿x方向的 . qU 电势能 重力势能 电场强度 3. 法拉第电磁感应定律 (1)E=n . (2)E= . 4. 电磁感应中的功能对应关系 (1) 电磁感应电路为纯电阻电路时产生的焦耳热等于 做的功 . (2) 电磁感应发生的过程 , 遵从能量守恒 , 焦耳热的增加量等于其他形式能量的 . Blv 克服安培力 减少量 热点考向一　动力学观点和能量观点解决电磁场问题 【 核心提炼 】 1. 动能定理在力学和电场中应用时的“ 3 同 1 异” 突破 热点考向聚焦 2. 带电粒子在复合场中的运动问题是典型的力电综合问题 , 一般要从受力、运动、功能的角度来分析 ; 此类问题所涉及的力有重力、电场力、磁场力、弹力、摩擦力等 , 涉及的运动形式有匀速直线运动、变速直线运动、曲线运动等 . 【 典例 1】 (2017 · 百校联盟模拟 ) 如图所示 , 在方向水平向左、范围足够大的匀强电场中 , 固定一由内表面绝缘光滑且内径很小的圆管弯制而成的圆弧 BD, 圆弧的圆心为 O, 竖直半径 OD=R,B 点和地面上 A 点的连线与地面成 θ=37° 角 , AB=R. 一质量为 m 、电荷量为 q 的小球 ( 可视为质点 ) 从地面上 A 点以某一初速度沿 AB 方向做直线运动 , 恰好无碰撞地从管口 B 进入管道 BD 中 , 到达管中某处 C( 图中未标出 ) 时恰好与管道间无作用力 . 已知 sin 37°=0.6,cos 37°=0.8, 重力加速度大小为 g. 求 : (1) 匀强电场的场强大小 E 和小球到达 C 处时的速度大小 v; 答案 : 见解析 (2)小球的初速度大小v 0 以及到达D处时的速度大小v D ; 答案 : 见解析 (3)若小球从管口D飞出时电场反向,则小球从管口D飞出后的最大水平射程x m . 答案 : 见解析 【 预测练习 1】 在竖直平面内放置一个由绝缘材料制作的管状圆环 , 管的内壁光滑 , 环的半径 R 远大于管的内径 , 如图所示 . 现以环的圆心为原点建立 xOy 平面坐标系 , 在第三象限内加一沿 x 轴正方向的匀强电场 , 整个空间有垂直环面向里的匀强磁场 . 一质量为 m 、带电荷量为 +q 的小球 ( 可视为质点 ) 在管内从 b 点由静止释放 , 小球直径略小于管的内径 . 重力加速度为 g. (1) 要使小球能沿绝缘管做圆周运动恰能到达最高点 a, 电场强度为多少 ? (2) 在 (1) 问的情况下 , 要使小球继续运动 , 第二次通过最高点 a 时 , 小球对绝缘管恰好无压力 , 匀强磁场的磁感应强度多大 ? (3) 如果场强大小、磁感应强度大小如 (1),(2) 问所求 , 将小球从 b 点由静止释放 , 求小球第 N 次经过最低点 c 时对管道的作用力 . 热点考向二　动力学观点和能量观点解决电磁感应问题 【 核心提炼 】 1.功能关系在力学和电磁感应中应用时的 “ 3同3异 ” 2.电磁感应中焦耳热的求法 【 典例 2】 (2017 · 江西新余模拟 ) 如图所示 , 两条光滑的金属导轨相距 L=1 m, 其中 MN 段平行于 PQ 段 , 位于同一水平面内 ,NN 0 段与 QQ 0 段平行 , 位于与水平面成倾角 37° 的斜面上 , 且 MNN 0 与 PQQ 0 均在竖直平面内 . 在水平导轨区域和倾斜导轨区域内分别有垂直于水平面和斜面的匀强磁场 B 1 和 B 2 , 且 B 1 =B 2 =0.5 T.ab 和 cd 是质量均为 m=0.1 kg 、电阻均为 R=4 Ω 的两根金属棒 ,ab 置于水平导轨上 ,cd 置于倾斜导轨上 , 均与导轨垂直且接触良好 . 从 t=0 时刻起 ,ab 棒在外力作用下由静止开始沿水平方向向右运动 (ab 棒始终在水平导轨上运动 , 且垂直于水平导轨 ),cd 受到 F=0.6-0.25t(N) 沿斜面向上的力的作用 , 始终处于静止状态 . 不计导轨的电阻 .(sin 37°=0.6,g 取 10 m/s 2 ) (1) 求流过 cd 棒的电流 I cd 随时间 t 变化的函数关系 ; (2) 求 ab 棒在水平导轨上运动的速度 v ab 随时间 t 变化的函数关系 ; 解析 : (1) 由题意知 cd 棒受力平衡 , 则 F+F cd =mgsin 37° F cd =B 2 I cd L, 得 I cd =0.5t(A). (2)ab 棒中电流 I ab =I cd =0.5t(A) 则回路中电源电动势 E=I cd R 总 ab 棒切割磁感线 , 产生的感应电动势为 E=B 1 Lv ab 解得 ab 棒的速度 v ab =8t(m/s) 所以 ,ab 棒做初速度为零的匀加速直线运动 . 答案 : (1)I cd =0.5t(A) (2)v ab =8t(m/s) (3) 求从 t=0 时刻起 ,1.0 s 内通过 ab 棒的电荷量 q; 答案 : (3)0.25 C (4) 若 t=0 时刻起 ,1.0 s 内作用在 ab 棒上的外力做功为 W=16 J, 求这段时间内 cd 棒产生的焦耳热 Q cd . 答案 : (4)6.4 J 【 预测练习 2】 (2017 · 江南十校二模 ) 如图 ,EFPMN 为光滑金属导轨 , 电阻不计 , 处于竖直平面内 , 其中 FP 倾斜 , 倾角为 θ,EF⊥FP,PMN 是半径为 R 的圆弧 , 圆弧与倾斜部分平滑连接于 P 点 ,N,M 分别为圆弧的最高点和最低点 , 还有一根与 EFPMN 完全相同的导轨 E′F′P′M′N′, 两导轨平行放置 , 间距为 L, 沿垂直于导轨所在平面的方向看去 , 两导轨完全重合 . 过 P 点的竖直线右侧有垂直于 FP 向上的匀强磁场 , 磁感应强度大小为 B, 两根相同的金属棒 ab,cd( 图中只画出了 a 端和 c 端 ), 质量为 m 、电阻为 r, 分别从导轨 FP 和 EF 上某位置由静止释放 , 在以后的过程中 ,ab,cd 始终与导轨保持垂直且接触良好 .( 轨道 FP 和 EF 足够长 , 题中所给的各个物理量均为已知 , 重力加速度为 g) (1) 若 ab 棒到达 P 点之前已经匀速运动 , 求 ab 棒匀速下滑时的速度 v, 以及此时 cd 棒的电功率 P; 答案 : (2) 不能运动到圆弧最高点 实战 高考真题演练 D 2. [ 应用动力学观点和能量观点解决电磁场问题 ] (2017 · 北京卷 ,22) 如图所示 , 长 l=1 m 的轻质细绳上端固定 , 下端连接一个可视为质点的带电小球 , 小球静止在水平向右的匀强电场中 , 绳与竖直方向的夹角 θ=37°. 已知小球所带电荷量 q=1.0×10 -6 C, 匀强电场的场强 E=3.0×10 3 N/C, 取重力加速度 g=10 m/s 2 , sin 37°=0.6,cos 37°=0.8. 求 : (1) 小球所受电场力 F 的大小 . (2) 小球的质量 m. (3) 将电场撤去 , 小球回到最低点时速度 v 的大小 . 解析 : (1)F=qE=3.0×10 -3 N. 答案 : (1)3.0×10 -3 N 　 (2)4.0×10 -4 kg 　 (3)2.0 m/s 3. [ 应用动力学观点和能量观点解决电磁感应问题 ] (2017 · 江苏卷 ,13) 如图所示 , 两条相距 d 的平行金属导轨位于同一水平面内 , 其右端接一阻值为 R 的电阻 . 质量为 m 的金属杆静置在导轨上 , 其左侧的矩形匀强磁场区域 MNPQ 的磁感应强度大小为 B 、方向竖直向下 . 当该磁场区域以速度 v 0 匀速地向右扫过金属杆后 , 金属杆的速度变为 v. 导轨和金属杆的电阻不计 , 导轨光滑且足够长 , 杆在运动过程中始终与导轨垂直且两端与导轨保持良好接触 . 求 : (1)MN 刚扫过金属杆时 , 杆中感应电流的大小 I; (2)MN 刚扫过金属杆时 , 杆的加速度大小 a; (3)PQ 刚要离开金属杆时 , 感应电流的功率 P. 4. [ 应用动力学观点和能量观点解决电磁感应问题 ] (2016 · 浙江卷 ,24) 小明设计的电磁健身器的简化装置如图所示 , 两根平行金属导轨相距 l=0.50 m, 倾角 θ= 53°, 导轨上端串接一个 R=0.05 Ω 的电阻 . 在导轨间长 d=0.56 m 的区域内 , 存 在方向垂直导轨平面向下的匀强磁场 , 磁感应强度 B=2.0 T. 质量 m=4.0 kg 的金属棒 CD 水平置于导轨上 , 用绝缘绳索通过定滑轮与拉杆 GH 相连 .CD 棒的初始位 置与磁场区域的下边界相距 s=0.24 m. 一位健身者用恒力 F=80 N 拉动 GH 杆 , CD 棒由静止开始运动 , 上升过程中 CD 棒始终保持与导轨垂直 . 当 CD 棒到达磁场上边界时健身者松手 , 触发恢复装置使 CD 棒回到初始位置 ( 重力加速度 g=10 m/s 2 ,sin 53°= 0.8, 不计其他电阻、摩擦力以及拉杆和绳索的质量 ). 求 (1)CD 棒进入磁场时速度 v 的大小 ; (2)CD 棒进入磁场时所受的安培力 F A 的大小 ; 答案 : (1)2.4 m/s 　 (2)48 N (3) 在拉升 CD 棒的过程中 , 健身者所做的功 W 和电阻产生的焦耳热 Q. 答案 : (3)64 J 　 26.88 J 点击进入 提升 专题限时检测