山东省师大附中2020届高三上学期10月阶段性检测 数学试题

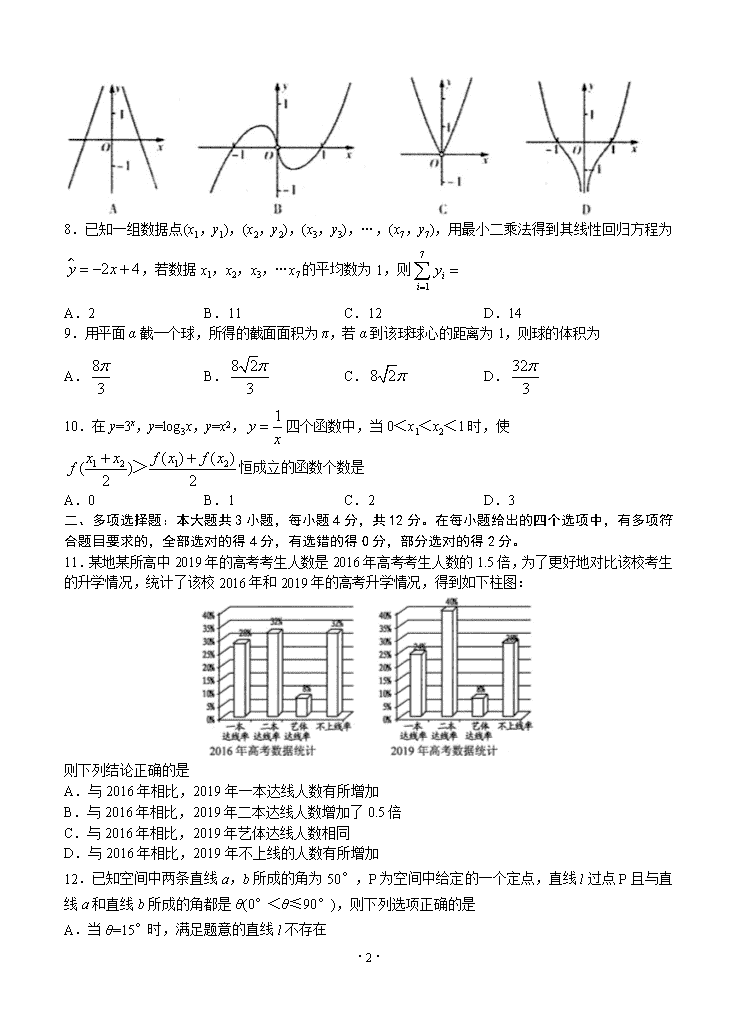
山东省师大附中2020届高三上学期10月阶段性检测 数学试题

山东省师大附中2020届高三上学期10月阶段性检测 数学试题 ‎2019．10‎ 本试卷共4页，共150分，考试时间120分钟 一、单项选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ l．已知集合，，若，则A∪B=‎ A． B． C． D．‎ ‎2．若实数x＞y，则 A．log0.5x＞log0.5y B． C．x2＞xy D．2x＞2y ‎3．设随机变量X~N(μ，7)，若P(X＜2)=P(X＞4)，则 A．μ=3，DX=7 B．μ=6，DX=‎ C．μ=3，DX= D．μ=6，DX=7‎ ‎4．设x∈R，则“｜x+1｜＜2”是“lgx＜0”的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎5．设x＞y＞0，x+y=1，若，，，，则实数a，b，c的大小关系是 A．a＜b＜c B．b＜a＜c C．b＜c＜a D．c＜b＜a ‎6．设α、β为两个不同的平面，l、m为两条不同的直线，且，，则下列命题中真命题是 A．若l⊥β，则α⊥β B．若l⊥m，则α⊥β C．若α⊥β，则l⊥m D．若α∥β，l∥m ‎7．函数的图象大致为 ‎·9·‎ ‎8．已知一组数据点(x1，y1)，(x2，y2)，(x3，y3)，…，(x7，y7)，用最小二乘法得到其线性回归方程为，若数据x1，x2，x3，…x7的平均数为1，则 A．2 B．11 C．12 D．14‎ ‎9．用平面α截一个球，所得的截面面积为π，若α到该球球心的距离为1，则球的体积为 A． B． C． D．‎ ‎10．在y=3x，y=log3x，y=x2，四个函数中，当0＜x1＜x2＜1时，使 恒成立的函数个数是 A．0 B．1 C．2 D．3‎ 二、多项选择题：本大题共3小题，每小题4分，共12分。在每小题给出的四个选项中，有多项符合题目要求的，全部选对的得4分，有选错的得0分，部分选对的得2分。‎ ‎11．某地某所高中2019年的高考考生人数是2016年高考考生人数的1.5倍，为了更好地对比该校考生的升学情况，统计了该校2016年和2019年的高考升学情况，得到如下柱图：‎ 则下列结论正确的是 A．与2016年相比，2019年一本达线人数有所增加 B．与2016年相比，2019年二本达线人数增加了0.5倍 C．与2016年相比，2019年艺体达线人数相同 D．与2016年相比，2019年不上线的人数有所增加 ‎12．已知空间中两条直线a，b所成的角为50°，P为空间中给定的一个定点，直线l过点P且与直线a和直线b所成的角都是θ(0°＜θ≤90°)，则下列选项正确的是 A．当θ=15°时，满足题意的直线l不存在 ‎·9·‎ B．当θ=25°时，满足题意的直线l有且仅有l条 C．当θ=40°时，满足题意的直线l有且仅有2条 D．当θ=60°时，满足题意的直线l有且仅有3条 ‎13．德国著名数学家狄利克雷在数学领域成就显著，是解析数论的创始人之一，以其名命名的函数，称为狄利克雷函数，则关于f(x)，下列说法正确的是 A．；‎ B．函数f(x)是偶函数：‎ C．任意一个非零有理数T，f(x+T) =f(x)对任意x∈R恒成立；‎ D．存在三个点A(x1，f(x1)，B(x2，f(x2)，C(x3，f(x3)，使得△ABC为等边三角形．‎ 三、填空题：本大题共4小题，每小题4分，共16分。把答案填在对应题号的横线上 ‎14．命题p：“，x2－πx≥0”的否定是___________________。‎ ‎15．已知f(x)为偶函数，当x≤0时，，则曲线y=f(x)在点（1,0）处的切线方程是______________________.‎ ‎16．甲、乙、丙、丁、戊5名同学参加“庆国庆70周年，爱国主义知识大赛”活动，决出第1名到第5名的名次。甲乙两名同学去询问成绩，回答者对甲说“虽然你的成绩比乙好，但是你俩都没得到第一名”；对乙说“你当然不会是最差的”从以上回答分析，丙是第一名的概率是_________________________。‎ ‎17．在棱长为6的正方体ABCD－A1B1C1D1中，M是BC的中点，点P是面DCC1D1所在的平面内的动点，且满足∠APD=∠MPC，则______________，三棱锥P－BCD的体积最大值是________________________________。‎ 四、解答题：本大题共6小题，共82分，解答应写出文字说明、证明过程或演算步骤 ‎18．(12分)已知定义域为R的函数，f(x)=ax－(k－1)a-x(a＞0且a≠1)是奇函数．‎ ‎(1)求实数k的值：‎ ‎(2)若f(1)＜0，判断函数单调性，并求不等式f(x2+tx)+f(4－x)＜0恒成立时t的取值范围；‎ ‎19．(14分)己知集合， ‎ ‎(1)求集合A、B；‎ ‎(2)当m＞0时，若x∈A是x∈B成立的充分不必要条作，求实数m的取值范围．‎ ‎·9·‎ ‎20．(14分)在直角梯形ABCD中，AB=BC=2，CD=4，BC⊥DC，AE⊥DC，M，N两点分别在线段AD，BE上运动，且DM=EN(如图1)．将三角形ADE沿AE折起，使点D到达D1的位置(如图2)，且平面D1AE⊥平面ABCE ‎(1)判断直线MN与平面D1CE的位置关系并证明；‎ ‎(2)证明：MN的长度最短时，M，N分别为AD1和BE的中点；‎ ‎(3)当MN的长度最短时，求平面D1MN与平面EMN所成角(锐角)的余弦值 ‎2l．(14分)某市城郊有一块大约500m×500m的接近正方形的荒地，地方政府准备在此建一个综合性休闲广场，首先要建设如图所示的一个矩形体育活动场地，其中总面积为3000‎ 平方米，其中阴影部分为通道，通道宽度为2米，中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同)，塑胶运动场地占地面积为S平方米．‎ ‎(1)分别用x表示y及S的函数关系式，并给出定义域；‎ ‎(2)请你设计规划该体育活动场地，使得该塑胶运动场地占地面积S最大，并求出最大值 ‎22．(14分)设函数f(x)=x2－(a－2)x－alnx ‎(1)求函数f(x)的单调区间；‎ ‎(2)若函数f(x)有两个零点，求正整数a的最小值 ‎23．(14分)某科技公司新开发一电子产品，该电子产品的一个系统G有3个电子元件组成，各个电子元件能否正常工作的概率均为，且每个电子元件能否正常工作相互独立，‎ 若系统G中有超过一半的电子元件正常工作，则G可以正常工作，否则就需要维修，且 维修所需要的费用为500元 ‎(1)求系统G不需要维修的概率；‎ ‎(2)该电子产品共由3个完全相同的系统G组成，设Y为电子产品需要维修的系统所需的费用，求Y的分布列与数学期望；‎ ‎(3)为提高系统G正常工作概率，在系统G内增加两个功能完全一样的其他品牌的电子元件，每个新元件正常工作的概率均为p，且新增元件后有超过一半的电子元件正常工作，则G可以正常工作，问：p满足什么条件时，可以提高整个系统G的正常工作概率?‎ ‎·9·‎ ‎2019-2020学年高三阶段性监测 数学参考答案 ‎ ‎2019.10‎ 一、单项选择题:本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎ 　1-5 CDABC 6-10 ADDBB 二、多项选择题:本大题共3小题，每小题4分，共12分.在每小题给出的四个选项中，有多项符合题目要求的.全部选对的得4分，有选错的得0分，部分选对的得2分.‎ ‎11.AD 12.ABC 13.ABCD 三、填空题：本大题共4小题，每小题4分，共16分.‎ ‎14. 15. 16. 17. 2； ‎ 四、解答题：本大题共6小题，共82分，解答应写出文字说明、证明过程或演算步骤.‎ ‎18．解：(1)∵是定义域为R的奇函数，‎ ‎∴ …… 2分 ‎∴. …… 4分 ‎（2）‎ ‎， ……6分 而在R上单调递减，在R上单调递增，‎ 故判断在R上单调递减， ……8分 不等式化为，，‎ ‎ 恒成立，‎ ‎，解得. ……12分 ‎19.解：（1）由，得. 故集合……2分 由，得，. ‎ ‎·9·‎ 当时，由得 故集合 ………4分 当时，由得：‎ 故集合 ………6分 当时，由得故集合 ………8分 ‎(2) 是成立的充分不必要条件，‎ 是的真子集， ………………………10分 则有，解得， …………………………12分 又当时，，不合题意，……………………13分 实数的取值范围为. ………………………14分 20. 解:（1）与平面平行. ………1分 证明如下：分别在平面和平面内作交于点，‎ 交于点，‎ 连接..设 在中，,‎ 则，‎ 同理可求，，‎ 即四边形是平行四边形. ..............3分 ‎.........4分 （2） 证明：平面平面，，.................5分 在中，‎ ‎·9·‎ ‎..........................7分 当时，.此时分别是和的中点...................8分 （2） 以为坐标原点，分别以所在直线为轴，建立如图所示的空 间直角坐标系，由题意知，，，‎ ‎.‎ ‎...................10分 设是平面的一个法向量，‎ 由可得.取，可得................11分 设是平面的一个法向量，‎ 由可得.取，可得.......................12分 ‎，‎ ‎∴平面与平面所成角（锐角）的余弦值. ......................14分 ‎21.解：（1）由已知其定义域是(6,500).……………2分 ‎,其定义域是(6,500).……………6分 ‎（2）‎ 当且仅当，即时，上述不等式等号成立，‎ 此时，‎ ‎·9·‎ 答：设计 时，运动场地面积最大，最大值为2430平方米.‎ ‎.………………………………………14分 ‎ ‎22.解:（1）....2分 当时，，函数在区间内单调递增，‎ 所以，函数的单调增区间为，无单调减区间；..............4分 当时，由，得；由，得.‎ 所以，函数的单调增区间为，单调减区间为. ..............6分 ‎（2）由（1）知：如果函数有两个零点，则，且，‎ 即，即：，...........................................8分 令 可知在区间内为增函数，且 ‎ .....................................................12分 所以存在 当时，；当时，.‎ 所以，满足条件的最小正整数 .....................................................14分 ‎23.解：（1）系统G不需要维修的概率为. …………2分 ‎（2）设为维修的系统G的个数，则，且，‎ 所以.………………4分 所以的分布列为 ‎0‎ ‎500‎ ‎1000‎ ‎1500‎ ‎·9·‎ 所以的期望为元………………………………6分 ‎（3）当系统有5个电子元件时，‎ 若前3个电子元件中有1个正常工作，同时新增的两个必须都正常工作，‎ 则概率为； ………………………8分 若前3个电子元件中有两个正常工作，同时新增的两个至少有1个正常工作，‎ 则概率为；……10分 若前3个电子元件中3个都正常工作，则不管新增两个元件能否正常工作，‎ 系统均能正常工作，则概率为. ………………………12分 所以新增两个元件后系统能正常工作的概率为 ‎，‎ 于是由知，当时，即时，‎ 可以提高整个系统的正常工作概率. ……………………………………14分 ‎·9·‎