2017年度中考数学（第27课时 解直角三角形及其应用）一轮复习学案

2017年度中考数学（第27课时 解直角三角形及其应用）一轮复习学案

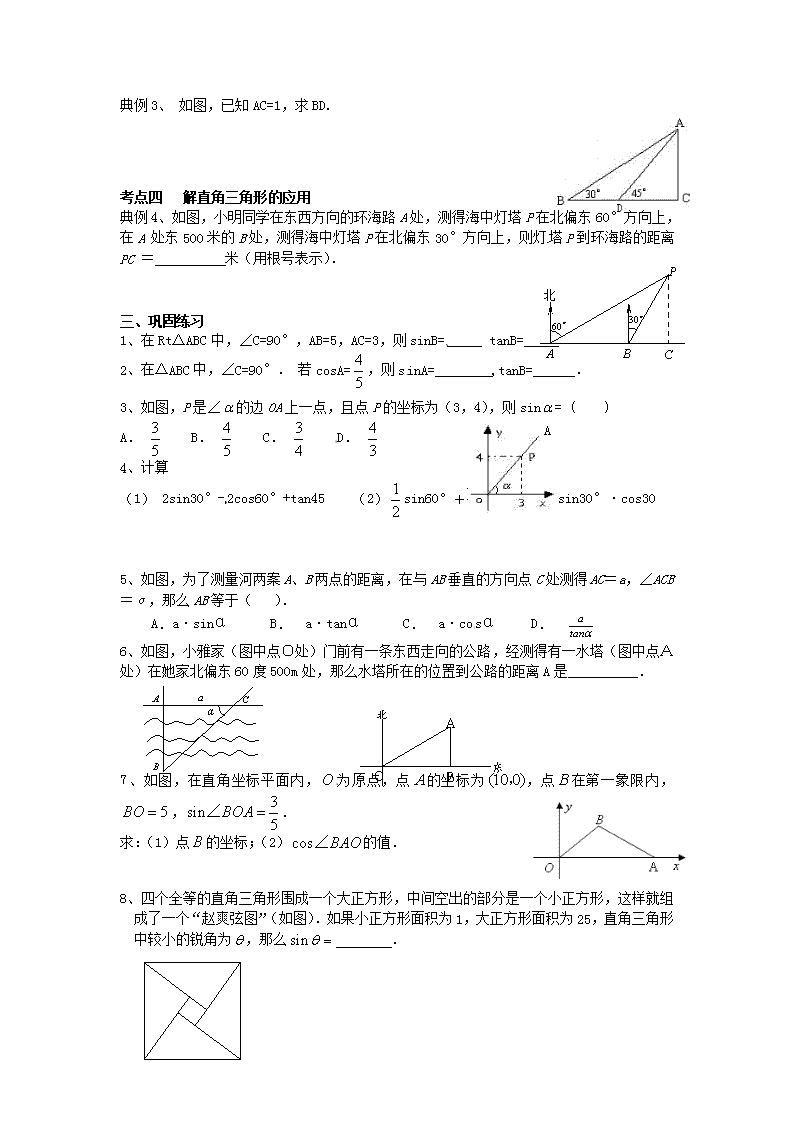
第27课时 解直角三角形及其应用 ‎【导学目标】‎ ‎1、理解锐角三角函数的概念，并准确记忆30°，45°，60°角的三角函数值。‎ ‎2、运用三角函数解决与直角三角形有关的简单实际问题。‎ ‎【导学过程】‎ 一、知识梳理 ‎1、锐角三角函数的定义：‎ 在Rt△ABC中，若∠A、∠B、∠C的对边分别为a、b、c，且∠C=90°，‎ ‎∠A的正弦sinA=； ‎ ‎∠A的余弦cosA=________；‎ ‎∠A的正切tanA=________.‎ ‎2、特殊的三角函数值 常见的特殊直角三角形：‎ ‎(1)含30°角的直角三角形：‎ ‎30°角所对的直角边是斜边的一半.三边之比_________________.‎ ‎(2)含45°角的直角三角形：‎ 等腰直角三角形，两直角边相等.三边之比___________________.‎ ‎3、坡度（坡比）、坡角 通常把坡面的________和________的比叫坡度（或坡比）,即坡面与水平面夹角的_________（填写哪个三角函数）‎ 二、典例分析 考点一 锐角三角函数的概念 考点三 解直角三角形 典例3、 如图，已知AC=1，求BD.‎ 考点四 解直角三角形的应用 P A B C ‎30°‎ ‎60°‎ 北 典例4、如图，小明同学在东西方向的环海路A处，测得海中灯塔P在北偏东60°方向上，在A 处东‎500米的B处，测得海中灯塔P在北偏东30°方向上，则灯塔P到环海路的距离PC ＝ 米（用根号表示）． ‎ 三、巩固练习 ‎1、在Rt△ABC中，∠C=90°，AB=5，AC=3，则sinB=_____ tanB=_____‎ ‎2、在△ABC中，∠C=90°． 若cosA=，则sinA=________,tanB=______．‎ A ‎3、如图，P是∠的边OA上一点，且点P的坐标为（3，4），则sin= ( )‎ A． B． C． D． ‎ ‎4、计算 ‎（1） 2sin30°-2cos60°+tan45 （2）sin60°＋ cos45°＋sin30°·cos30‎ ‎5、如图，为了测量河两案A、B两点的距离，在与AB垂直的方向点C处测得AC＝a，∠ACB＝α，那么AB等于（ ）．‎ A．a·sinα B． a·tanα C． a·cosα D． ‎ ‎6、如图，小雅家（图中点Ｏ处）门前有一条东西走向的公路，经测得有一水塔（图中点Ａ处）在她家北偏东60度‎500m处，那么水塔所在的位置到公路的距离A是__________．‎ A O B 东 北 A B C a α ‎7、如图，在直角坐标平面内，为原点，点的坐标为，点在第一象限内，，．‎ 求：（1）点的坐标；（2）的值．‎ ‎8、四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”（如图）．如果小正方形面积为1，大正方形面积为25，直角三角形中较小的锐角为，那么 ．‎ ‎9、如图，小明用一块有一个锐角为的直角三角板测量树高，已知小明离树的距离为‎4米，DE为‎1.68米，那么这棵树大约有多高？（精确到‎0.1米）‎ ‎10、直角三角形纸片的两直角边长分别为6，8，现将如图那样折叠，使点与点重合，折痕为，求的值。‎ ‎6‎ ‎8‎ C E A B D