- 2024-05-24 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
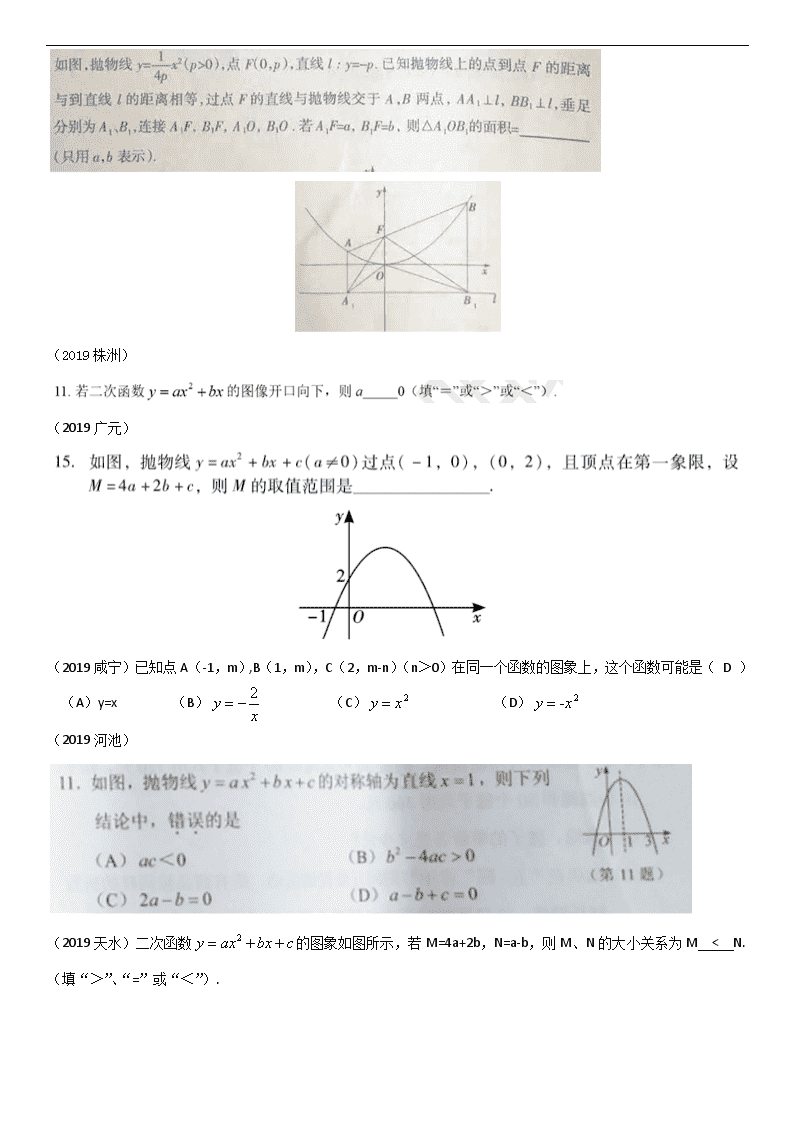
2019年全国中考真题分类汇编:二次函数的图象与性质
(分类)第12讲 二次函数 第1课时 二次函数的图象与性质 知识点1 二次函数的概念 知识点2 二次函数的图象与性质 知识点3 二次函数图象的平移 知识点4 确定二次函数的解析式 知识点5 二次函数与方程、不等式 知识点1 二次函数的概念 知识点2 二次函数的图象与性质 (2019荆州) (2019哈尔滨) (2019河南) (2019长春) (2019大庆) (2019株洲) (2019广元) (2019咸宁)已知点A(-1,m),B(1,m),C(2,m-n)(n>0)在同一个函数的图象上,这个函数可能是( D ) (A)y=x (B) (C) (D) (2019河池) (2019天水)二次函数的图象如图所示,若M=4a+2b,N=a-b,则M、N的大小关系为M < N.(填“>”、“=”或“<”). (2019兰州) (2019陇南) (2019无锡)某个函数具有性质:当>0时,随的增大而增大,这个函数的表达式可以是y=x2(答案不唯一).(只要写出一个符合题意的答案即可). (2019衢州)二次函数图象的顶点坐标是( A ) (2019重庆B卷)抛物线y=-3x2+6x+2的对称轴是( C ) A、直线x=2 B、直线x=-2 C、直线x=1 D、直线x=-1. (2019遂宁) (2019泰安) (2019温州)已知二次函数,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是(D) A.有最大值﹣1,有最小值﹣2 B.有最大值0,有最小值﹣1 C.有最大值7,有最小值﹣1 D.有最大值7,有最小值﹣2 (2019德州)在下列函数图象上任取不同两点P1(x1,y1)、P2(x2,y2),一定能使成立的是( D ) (2019泸州)已知二次函数(其中是自变量)的图象与轴没有公共点,且当时,随的增大而减小,则实数的取值范围是( D ) A. B. C. D. (2019福建)若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(, y2)、E(2,y3),则y1、y2、y3的大小关系是( D ) A. y1< y2< y3 B. y1 < y3< y2 C. y3< y2< y1 D. y2< y3< y1 (2019云南)已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点. (1)求k的值; (2)若点P在物线y=x2+(k2+k-6)x+3上,且P到y轴的距离是2,求点P的坐标. (2019宁波)如图,已知二次函数的图象经过点P(-2,3). (1)求a的值和图象的顶点坐标; (2)点Q(m,n)在该二次函数图象上. ①当m=2时,求n的值; ②若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围. (2019长春) (2019北京) (2019仙桃)在平面直角坐标系中,已知抛物线C:y=ax2+2x-1(a≠0)和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上. (1)若抛物线C与直线l有交点,求a的取值范围; (2)当a=-1,二次函数y=ax2+2x-1的自变量x满足m≤x≤m+2时,函数y的最大值为-4, 求m的值; 数学试卷 第8页(共8页) (3)若抛物线C与线段AB有两个不同的交点,请直接写出a的取值范围. (2019温州)如图,在平面直角坐标系中,二次函数的图象交x轴于点A,B(点A在点B的左侧). (1)求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围; (2)把点B向上平移m个单位得点B1.若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1向左平移(n+6)个单位,将与该二次函数图象上的点B3重合.已知m>0,n>0,求m,n的值. (2019台州) (2019安徽)22.一次函数y=kx+4与二次函数y=ax2+c的图像的一个交点坐标为(1,2),另一个交点是该二次函数图像的顶点 (1)求k,a,c的值; (2)过点A(0,m)(0<m<4)且垂直于y轴的直线与二次函数y=ax2+c的图像相交于B,C两点,点O为坐标原点,记W=OA2+BC2,求W关于m的函数解析式,并求W的最小值. 解:(1)由题意得,k+4=-2,解得k=-2,又二次函数顶点为(0,4),∴c=4 把(1,2)带入二次函数表达式得a+c=2,解得a=-2 (2) 由(1)得二次函数解析式为y=-2x2+4,令y=m,得2x2+m-4=0 ∴,设B,C两点的坐标分别为(x1,m)(x2,m),则, ∴W=OA2+BC2= ∴当m=1时,W取得最小值7. (2019金华) (2019威海) (2019长沙) (2019江西) (2019杭州)设二次函数是实数). (1) 甲求得当时,;当时,;乙求得当时,,若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由. (2) 写出二次函数图象的对称轴,并求该函数的最小值(用含的代数式表示). (3) 已知二次函数的图象经过(0,m)和(1,n)两点(m,n是实数),当时,求证:. (2019广州)已知抛物线G:有最低点。 (1) 求二次函数的最小值(用含m的式子表示); (2) 将抛物线G向右平移m个单位得到抛物线G1。经过探究发现,随着m的变化,抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围; (3) 记(2)所求的函数为H,抛物线G与函数H的图像交于点P,结合图像,求点P的纵坐标的取值范围. (4) (1)-3-m (5) (2)y= -x -2(x>1) (1) 知识点3 二次函数图象的平移 (2019济宁)答案:D (2019绍兴)在平面直角坐标系中,抛物线经过变换后得到抛物线,则这个变换可以是 ( B ) A.向左平移2个单位 B.向右平移2个单位 C.向左平移8个单位 D.向右平移8个单位 (2019玉林) (2019哈尔滨) (2019凉山州)将抛物线向左平移______个单位后经过点A(2,2). (2019宜宾) 知识点4 确定二次函数的解析式 (2019遂宁) (2019泰州) (2019龙东) 知识点5 二次函数与方程、不等式 (2019武汉)抛物线y=ax2+bx+c经过点A(-3,0)、B(4,0)两点,则关于x的一元二次方程a(x-1)2+c=b-bx的解是____x1=-2,x2=5______. (2019潍坊) (2019凉山州)当时,直线与抛物线有交点,则的取值范围是____________. (2019杭州)在平面直角坐标系,已知,设函数的图象与x轴有M个交点,函数的图象与x轴有N个交点,则( C ) A.M=N-1或M=N+1 B.M=N-1或M=N+2 C.M=N或M=N+1 D.M=N或M=N-1 (2019资阳) (2019荆门)答案:C (2019济宁)答案: (2019安徽)14.在平面直角坐标系中,垂直于x轴的直线l分别于函数y=x-a+1和y+x2-2ax的图像相交于P,Q两点.若平移直线l,可以使P,Q都在x轴的下方,则实数a的取值范围是 a>1或a<-1 . (2019凉山州) (2019湖州)已知抛物线与x轴有两个不同的交点. (1) 求c的取值范围; (2) 若抛物线经过点A(2,m)和点B(3,n),试比较m与n的大小,并说明理由.查看更多