2019年南昌一模理科数学(解析版)

2019年南昌一模理科数学(解析版)

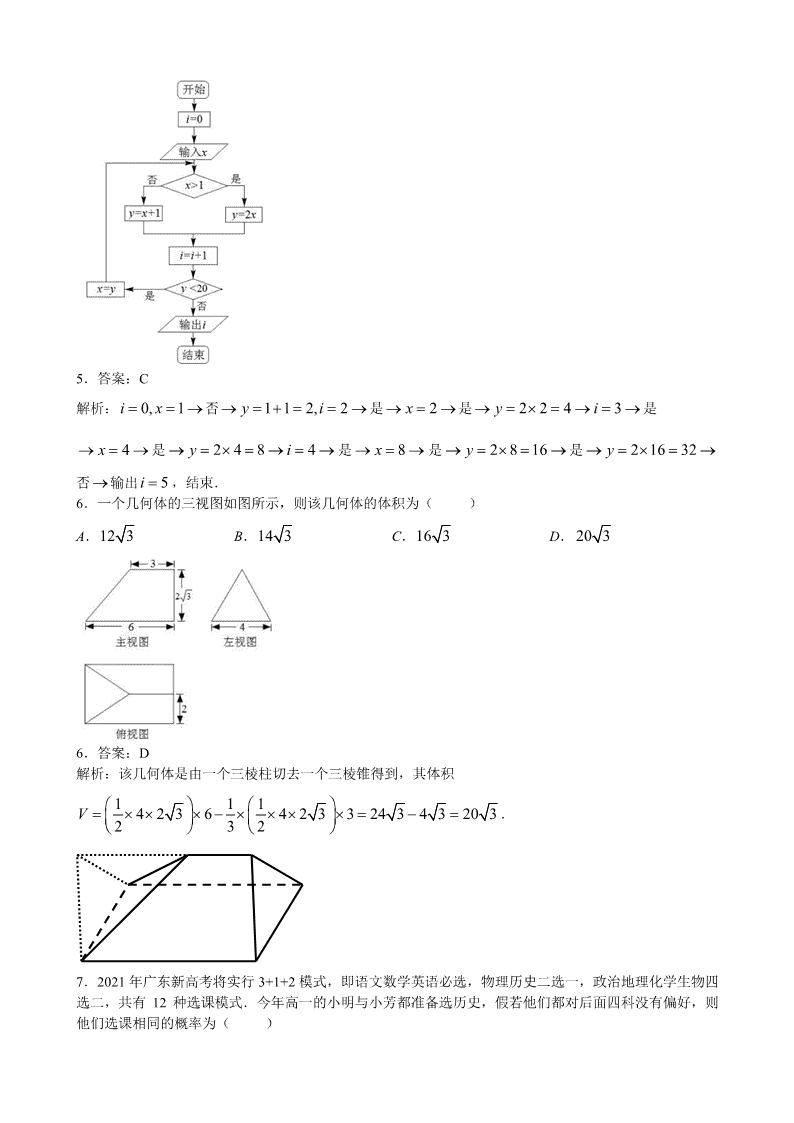
NCS20190607 项目第一次模拟测试卷 理科数学 一、选择题：本题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有一项是符合题目 要求的． 1．设集合 2 2{ | 4 0}, { | log 1}M x x N x x     ，则 R M N  （ ） A． B．(0, 2) C．( 2,2) D．[ 2, 2) 1．答案：B 解析： 2 2{ | 4 0} { | 2 2}, { | log 1} { | 0 2}M x x x x N x x x x        R ≤ ≤ ≤ ， 所以  (0,2)M N R  ． 2．已知复数 i ( )2i Raz a  的实部等于虚部，则 a （ ） A． 1 2 B． 1 2 C． 1 D．1 2．答案：C 解析： 2 i ( i) i 1 i 1 i2i 2i 2 2 2 a a a az          ．根据题意可得 1 2 2 a  ，所以 1a   ． 3．已知抛物线方程为 2 2x y  ，则其准线方程为（ ） A． 1y   B． 1y  C． 1 2y  D． 1 2y   3．答案：C 解析：抛物线开口向下， 11, 2 2 pp   ，所以其准线方程为 1 2y  ． 4．已知{ }na 为等差数列，若 2 3 4 32 1, 2 7a a a a    ，则 5a  （ ） A．1 B．2 C．3 D．6 4．答案：B 解析： 4 2 2 6, 3a a d d     ，所以 2 3 22 1 2( 3) 1a a a     ，解得 2 7a   ， 所以 5 2 3 7 9 2a a d      ． 5．如图所示算法框图，当输入的 x 为 1 时，输出的结果为（ ） A．3 B．4 C．5 D．6 5．答案：C 解析： 0, 1i x  否 1 1 2, 2y i      是 2x  是 2 2 4 3y i       是 4x   是 2 4 8 4y i       是 8x   是 2 8 16y     是 2 16 32y     否 输出 5i  ，结束． 6．一个几何体的三视图如图所示，则该几何体的体积为（ ） A．12 3 B．14 3 C．16 3 D． 20 3 6．答案：D 解析：该几何体是由一个三棱柱切去一个三棱锥得到，其体积 1 1 14 2 3 6 4 2 3 3 24 3 4 3 20 32 3 2V                      ． 7．2021 年广东新高考将实行 3+1+2 模式，即语文数学英语必选，物理历史二选一，政治地理化学生物四 选二，共有 12 种选课模式．今年高一的小明与小芳都准备选历史，假若他们都对后面四科没有偏好，则 他们选课相同的概率为（ ） A． 1 36 B． 1 16 C． 1 8 D． 1 6 7．答案：D 解析：所求概率 2 4 2 2 4 4 1 1 6 CP C C   ． 8．已知 0, , Rr x y  ， 2 2 212 ≤ ≤yp x q x y r ：“ ”, ：“ ” ，若 p 是 q 的必要不充分条件，则实 数 r 的取值范围是（ ） A． 2 50, 5      B．(0,1] C． 2 5 ,5     D．[2, ) 8．答案：A 解析：如图，命题 p 所代表的集合为菱形 ABCD 及其内部，其中 ( 1,0), (0,2), (1,0), (0, 2)A B C D  ， 命题 q 所代表的集合为以O 为圆心，r 为半径的圆及其内部，因为 p 是 q 的必要不充分条件，所以 O 在 菱形 ABCD 内部，因为点O 到直线 AB 的距离为1 2 2 5 55   ，所以实数 r 的取值范围是 2 50, 5      ． x y OA B C D 9．已知 ( )f x 在 R 上连续可导， ( )f x 为其导函数，且 ( ) (1) ( )x x x xf x e e f x e e      ，则 (2) ( 2) (0) (1)f f f f       （ ） A． 2 24 4e e B． 2 24 4e e C．0 D． 24e 9．答案：C 解析： ( ) (1)[( ) ( )] (1 (1))( ) (1)( )x x x x x x x x x xf x e e f e e x e e f e e x f e e                   ， 可知 ( )f x 为奇函数，所以 (2) ( 2) 0, (0) 0, (2) ( 2) (0) (1) 0f f f f f f f               ． 10．已知平面向量 , , (2cos , 2sin ), (cos ,sin )   a b a b     ，若对任意的正实数  ， a b  的最小 值为 3 ，则此时 a b   （ ） A．1 B．2 C． 2 D． 3 10．答案：D 解析：设 (2cos ,2sin ), (cos ,sin )OA a OB b          ，则点 A 在以O 为圆心，半径为 2 的圆上， 点 B 在单位圆上， AOB     ，设 ( 0)OC b     ，则点C 在射线OB 上， 此时 a b OA OC CA        ，显然，当 AC OB 时，CA  最小，最小值为 3 ，可知 3sin 2AOB  ， 60AOB   ，此时 ,B C 两点重合， 3a b OA OB BA         ． B(C) O A 11．已知 ( 3,0), ( 3,0)A B ，P 为圆 2 2 1x y  上的动点，AP PQ   ，过点 P 作与 AP 垂直的直线l 交 直线QB 于点 M ，则 M 的横坐标范围是（ ） A． 1≥x B． 1x  C． 2≥x D． 2 2 ≥x 11．答案：A 解析： PM 是线段 AQ 的垂直平分线，所以 AM MQ ， 所以 2 2AM BM MQ BM BQ OP      ，或 2 2BM AM BQ OP    ， 所以点 M 在以 ,A B 为焦点的双曲线上， 2 2 22 2, 1, 3, 2a a c b c a      ， 所以双曲线方程为 2 2 12 yx   ，所以 1≥x ． M Q BA O P M Q BA O P 12．杨辉三角，是二项式系数在三角形中的一种几何排列．在欧洲，这个表叫做帕斯卡三角形，帕斯卡（1623 —1662）是在 1654 年发现这一规律的．我国南宋数学家杨辉在 1261 年所著的《详解九章算法》一书中出 现了如图所示的表，这是我国数学史上的一次伟大成就．如图所示，在“杨辉三角”中，去除所有为 1 的 项，依次构成数列 2,3,3,4,6, 4,5,10,10,5, ，则此数列前 135 项的和为（ ） A． 182 53 B． 182 52 C． 172 53 D． 172 52 12．答案：A 解析：如图，第 n 行的所有数字之和为 12 2n  ，前 n 行共有 ( 1) 2 n n  个数字，当 16n  时， ( 1) 1362 n n   ， 所以此数列前 135 项的和为 2 3 17 2 3 17 18 18(2 2) (2 2) (2 2) 17 (2 2 2 ) 32 17 2 4 32 17 2 53                    2 3 3 4 6 4 5 10 10 5 ……………… 二、填空题：本题共 4 小题，每小题 5 分，共 20 分．把答案填在题中的横线上． 13．设函数 2 2 , ( 0)( ) ( 3), ( 0) xx xf x f x x      ≤ ，则 (5)f 的值为 ． 13．答案： 1 2 解析： 2 1 1 1(5) (2) ( 1) ( 1) 2 1 2 2f f f          ． 14．侧面为等腰直角三角形的正三棱锥的侧棱与底面所成角的正弦值为 ． 14．答案： 3 3 解析：如图，在棱长为 1 的正方体 1 1 1 1ABCD A B C D 中， 三棱锥 1A A BD 即为侧面为等腰直角三角形的正三棱锥， 连接 1AC ，交平面 1A BD 于点 P ，交平面 1 1B CD 于点Q ， 则 1AC  平面 1A BD ，且 ,P Q 为 1AC 的三等分点， A C B D B1 C1 D1 A1 P Q 3 3AP  ， 3sin 3 APADP AD   ． 15．已知锐角 A 满足方程3cos 8tan 0A A  ，则 cos 2A  ． 15．答案： 7 9 解析：由3cos 8tan 0A A  ，可得 23cos 8sin 0A A  ，即 23sin 8sin 3 0A A    ， 23sin 8sin 3 0A A   ， (3sin 1)(sin 3) 0A A   ，又因为 A 为锐角，所以 1sin 3A  ， 则 2 7cos 2 1 2sin 9A A   ． 16．定义在封闭的平面区域 D 内任意两点的距离的最大值称为平面区域 D 的“直径” ．已知锐角三角形 的三个顶点 , ,A B C 在半径为 1 的圆上，且 3BAC   ，分别以 ABC△ 各边为直径向外作三个半圆，这 三个半圆和 ABC△ 构成平面区域 D ，则平面区域 D 的“直径”的最大值是 ． 16．答案： 3 3 2 解析：设角 , ,A B C 的对边为 , ,a b c ，平面区域 D 的“直径”为 d ，由正弦定理得 2 2sin a RA   ， 2sin 3a A   ，如图，设 ,E F 为 ,AB AC 的中点，直线 EF 与两个半圆分别交于 ,M N 两点，则 1 ( )2d MN ME EF FN c a b       ，在 ABC△ 中，由余弦定理得 2 2 2 2 2 2 2 2 2 3( ) ( )2 cos ( ) 3 ( ) 4 4 b c b ca b c bc A b c bc b c bc b c             ≥ ， 所以 2 2( ) 4 12b c a ≤ ，所以 3 32 3, 3 3, 2 2 a b cb c a b c d     ≤ ≤ ≤ ， 当且仅当b c 时等号成立． NM E F O CB A NM E F O CB A 三、解答题：共 70 分．解答应写出文字说明、证明过程或演算步骤．第 17~21 题为必考题，每个试题考 生都必须作答．第 22、23 题为选考题，考生根据要求作答． （一）必考题：共 60 分． 17．（本小题满分 12 分）函数 ( ) 2sin( ) 0 ,2 2f x x             的部分图象如下图所示， (0, 3), (2,0)A C ，并且 //AB x 轴． （1）求 和 的值； （2）求cos ACB 的值． 17．【解析】（Ⅰ）由已知 3sin2)0(  f ， 又| | 2  ，所以 3  ，所以 )3sin(2)(   xxf ………3 分 由 (2) 0f  ，即 2sin(2 ) 03    ，所以 2 3 k   ， k Z ， 解得 2 6 k    ， k Z ，而0 2   ，所以 3   . ………6 分 （Ⅱ）由（Ⅰ）知， )33sin(2)(   xxf ， 令 ( ) 3f x  ， 得 23 3 3x k     或 223 3 3x k     ， Zk  ， 所以 6x k 或 6 1x k  ，由图可知， (1, 3)B . ………8 分 所以 )3,1(),3,2(  CBCA ，所以 7, 2CA CB    ， ………10 分 所以 5 5 7cos 142 7 CA CBACB CA CB          . ……………………………………………12 分 18．（本小题满分 12 分） 如图，四棱台 1 1 1 1ABCD A B C D 中，底面 ABCD 是菱形， 1CC  底面 ABCD ，且 60BAD   ， 1 1 12 4,CD CC C D E   是棱 1BB 的中点． （1）求证： 1AA BD ； （2）求二面角 1 1E AC C  的余弦值． A B CD D1 C1A1 B1 E 18．【解析】（Ⅰ）证明：因为 1CC 底面 ABCD ，所以 BDCC 1 . 因为底面 ABCD 是菱形，所以 ACBD  . 又 CCCAC 1 ，所以 BD 平面 1ACC .………3 分 又由四棱台 1111 DCBAABCD  知， 11 ,,, CCAA 四点共面. 所以 1AABD  . ………5 分 （Ⅱ）如图，设 AC 交 BD 于点O ，依题意， OCCA //11 且 OCCA 11 ， 所以 11 //CCOA ，且 11 CCOA  . 所以 OA1 底面 ABCD . 以O 为原点， 1, ,OA OB OA 所在直线分别为 x 轴、 y 轴、 z 轴建立空间直角坐标系. 则 1 1(2 3,0,0), (0,0,4), ( 2 3,0,4), (0,2,0)A A C B ， 由 1 1 1 2A B AB    得， 1( 3,1,4)B  ．因为 E 是棱 1BB 的中点，所以 3 3, , 22 2E      ．………8 分 所以 1 1 1 3 3, , 2 , ( 2 3,0,0)2 2EA AC          . 设 1 ( , , )n x y z  为平面 1 1EAC 的法向量，则 1 1 1 1 1 2 3 0 3 3 2 02 2 n AC x n EA x y z               ， 取 3z  ，则 1 (0,4,3)n   . 又因为 2 (0,1,0)n   为平面 1 1AC C 的法向量， 所以 1 2 1 2 1 2 4cos , 5 n nn n n n         ， 又由图可知，二面角 1 1E AC C  为锐二面角， 所以二面角 1 1E AC C  的余弦值为 4 5 . ……………………………………………12 分 19．（本小题满分 12 分） 市面上有某品牌 A 型和 B 型两种节能灯，假定 A 型节能灯使用寿命都超过 5000 小时．经销商对 B 型节能 灯使用寿命进行了调查统计，得到如下频率分布直方图： 某商家因原店面重新装修，需租赁一家新店面进行周转，合约期一年．新店面需安装该品牌节能灯 5 支（同 种型号）即可正常营业．经了解，A 型 20 瓦和 B 型 55 瓦两种节能灯照明效果相当，都适合安装．已知 A 型和 B 型节能灯每支的价格分别为 120 元、25 元，当地商业电价为 0.75 元/千瓦时．假定该店面正常营业 一年的照明时间为 3600 小时，若正常营业期间灯坏了立即购买同型灯更换．（用频率估计概率） （1）若该商家新店面全部安装了 B 型节能灯，求一年内恰好更换了 2 支灯的概率； （2）若只考虑灯的成本和消耗电费，你认为商家应该选择哪种型号的节能灯，请说明理由． 19．【解析】（Ⅰ）由频率分布直方图可知， B 型节能灯使用寿命超过3600 小时的频率为 2.0 ， 用频率估计概率，得 B 型节能灯使用寿命超过3600 小时的概率为 5 1 . 所以一年内一支 B 型节能灯在使用期间需更换的概率为 5 4 ，. ………3 分 所以一年内 5 支恰好更换了 2 支灯的概率为 2 2 3 5 4 1 32( ) ( )5 5 625C   .. ………5 分 （Ⅱ）共需要安装5 支同种灯管， 若选择 A 型节能灯，一年共需花费 35 120 3600 5 20 0.75 10 870       元；………7 分 若选择 B 型节能灯，由于 B 型节能灯一年内需更换灯的支数服从二项分布 4(5, )5B ， 故一年需更换灯的支数的期望为 45 45  支， ………9 分 故一年共需花费 34(5 5) 25 3600 5 55 0.75 10 967.55         元. ………11 分 因为967.5 870 ，所以该商家应选择 A 型节能灯. ………………………………………12 分 20．（本小题满分 12 分）如图，椭圆 2 2 2 2: 1( 0)x yE a ba b    与圆 2 2: 1O x y  相切，并且椭圆 E 上 动点与圆O 上动点间距离的最大值为 2 6 2  ． （1）求椭圆 E 的方程； （2）过点 (1,0)N 作两条互相垂直的直线 1 2,l l ， 1l 与 E 交于 ,A B 两点， 2l 与圆O 的另一交点为 M ，求 ABM△ 面积的最大值，并求取得最大值时直线 1l 的方程． x M y A B O N 20．【解析】（Ⅰ）椭圆 E 与圆O ： 2 2 1x y  相切，知 2 1b  ； ……………………………2 分 又椭圆 E 上动点与圆O 上动点间距离最大值为 2 6 2  ，即椭圆中心O 到椭圆最远距离为 6 2 ， 得椭圆长半轴长 6 2a  ，即 2 3 2a  ； 所以轨迹 E 的方程为 2 22 13 x y  . ……………………………………………………………5 分 （Ⅱ）①当 1l 与 x 轴重合时， 2l 与圆相切，不合题意. ②当 xl 1 轴时， )0,1(M ， 1:1 xl ， 3AB  ，此时 1 2 3 2 322 3 3ABMS    △ .…6 分 ③当 1l 的斜率存在且不为0 时，设 1:1  myxl ， 0m ，则 11:2  ymxl ， 设 ),(),,( 2211 yxByxA ，由 2 2 1, 2 13 x my x y     得， 2 2(2 3) 4 1 0m y my    ， 所以 1 2 1 22 2 4 1,2 3 2 3 my y y ym m      ， ……………8 分 所以 2 2 2 2 1 2 2 3 1 2 11 2 3 m mAB m y y m       . 由      1 ,11 22 yx ymx 得， 02)11( 2 2  ymym ，解得 1 2 2  m myM ， …………9 分 所以 2 2 1 21 1MMN ym m     ， 所以 2 2 2 2 1 1 2 3 1 2 1 2 2 2 2 3 1ABM m mS AB MN m m       △ 2 2 2 2 2 3 2 1 2 3 22 3 2 1 2 1 m m m m      ， ……………10 分 因为 22 1 1m   ， 所以 2 2 22 1 2 2 2 1 m m    ≥ ， 当且仅当 2 2m   时取等号. 所以 6 2ABMS△ ≤ （ 2 3 6 3 2 ） 综上， ABM△ 面积的最大值为 6 2 ，此时直线 1l 的方程为 2 12x y   . ……………12 分 21．（本小题满分 12 分）已知函数 ( ) ( ln )xf x e x x a    （ e 为自然对数的底数，a 为常数，且 1a ≤ ） （1）判断函数 ( )f x 在区间(1, )e 内是否存在极值点，并说明理由； （2）若当 ln 2a  时， ( ) ( )f x k k Z  恒成立，求整数 k 的最小值． 21．【解析】（Ⅰ） )11(lne)(  axxxxf x ， ……………2 分 令 )e,1(,11ln)(  xaxxxxg ，则 )(e)( xgxf x ， 01)( 2 2  x xxxg 恒成立，所以 )(xg 在 )e,1( 上单调递减， ……………4 分 所以 ( ) (1) 1 0g x g a   ≤ ，所以 ( ) 0f x  在 )e,1( 内无解. 所以函数 )(xf 在区间 )e,1( 内无极值点. ……………5 分 （Ⅱ）当 2lna 时， )2lnln(e)(  xxxf x ，定义域为 ),0(  ， )12ln1(lne)(  xxxxf x ，令 12ln1ln)(  xxxxh ， ……………6 分 由（Ⅰ）知， )(xh 在 ),0(  上单调递减，又 02 1)2 1( h ， 012ln)1( h ， 所以存在 )1,2 1(1 x ，使得 0)( 1 xh ，且当 ),0( 1xx 时， 0)( xh ，即 0)(  xf ， 当 ),( 1  xx 时， 0)( xh ，即 0)(  xf . ……………8 分 所以 )(xf 在 ),0( 1x 上单调递增，在 ),( 1 x 上单调递减， 所以 )2lnln(e)()( 111max 1  xxxfxf x . ……………9 分 由 0)( 1 xh 得 012ln1ln 1 11  xxx ，即 1 11 112lnln xxx  ， 所以 )11(e)( 1 1 1 xxf x  ， )1,2 1(1 x ……………10 分 令 )1,2 1(),11(e)(  xxxr x ，则 0)111(e)( 2  xxxr x 恒成立，所以 )(xr 在 )1,2 1( 上 单调递增，所以 1e ( ) ( ) (1) 02r r x r     ，所以 0)( max xf ，………11 分 又因为 12 e)2ln2ln2 1(e)2 1( 2 1 f ， 所以 0)(1 max  xf ， 所以若 )()( Zkkxf  恒成立，则 k 的最小值为0 . …12 分 （二）选考题：共 10 分．请考生在第 22、23 题中任选一题作答．如果多做，则按所作的第一题计分． 22．【选修 4—4：坐标系与参数方程】（本小题满分 10 分） 在平面直角坐标系 xOy 中，直线l 的参数方程为 2 1 3 x t y t     （t 为参数），曲线C 的参数方程为 4 2cos 3 2sin x y        （ 为参数），以坐标原点为极点， x 轴非负半轴为极轴建立极坐标系． （1）求C 的极坐标方程； （2）设点 (2,1)M ，直线l 与曲线C 相交于点 ,A B ，求 MA MB 的值． 22．【解析】（Ⅰ）由参数方程        sin23 cos24 y x ，得普通方程 2 2( 4) ( 3) 4x y    ， 所以极坐标方程 2 8 cos 6 sin 21 0        . ……………5 分 （Ⅱ）设点 ,A B 对应的参数分别为 1t 、 2t ，将      ty tx 31 ,2 代入 2 2( 4) ( 3) 4x y    得 01)13(2  tt ， 所以 121 tt ， ……………8 分 直线      ty txl 31 ,2: （t 为参数）可化为        )2(2 31 ),2(2 12 ty tx ， 所以 1 2 1 22 2 4 4MA MB t t t t     . ……………10 分 23．【选修 4—5：不等式选讲】（本小题满分 10 分） 已知函数 2( ) 2 3f x x m x m     ． （1）求证： ( ) 2≥f x ； （2）若不等式 (2) 16f ≤ 恒成立，求实数 m 的取值范围． 23．【解析】（Ⅰ）因为 2 2( ) 2 3 ( ) ( 2 3)f x x m x m x m x m≥         ， 所以 2 2( ) 2 3 ( 1) 2 2f x m m m    ≥ ≥ . ……………5 分 （Ⅱ）由已知， |12|2)2( 2  mmf ， ①当 1 2 ≥m  时， (2) 16f ≤ 等价于 2 2 3 16m m  ≤ ，即 2( 1) 14m  ≤ ， 解得 14 1 14 1m  ≤ ≤ ，所以 1 14 12 m ≤ ≤ ； ……………7 分 ②当 2 1m 时， (2) 16f ≤ 等价于 2 2 1 16m m  ≤ ， 解得 3 5m ≤ ≤ ，所以 13 2m  ≤ . ……………9 分 综上，实数 m 的取值范围是 ]114,3[  . ……………10 分