- 2024-05-12 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018咸阳市第二次模拟文数试题
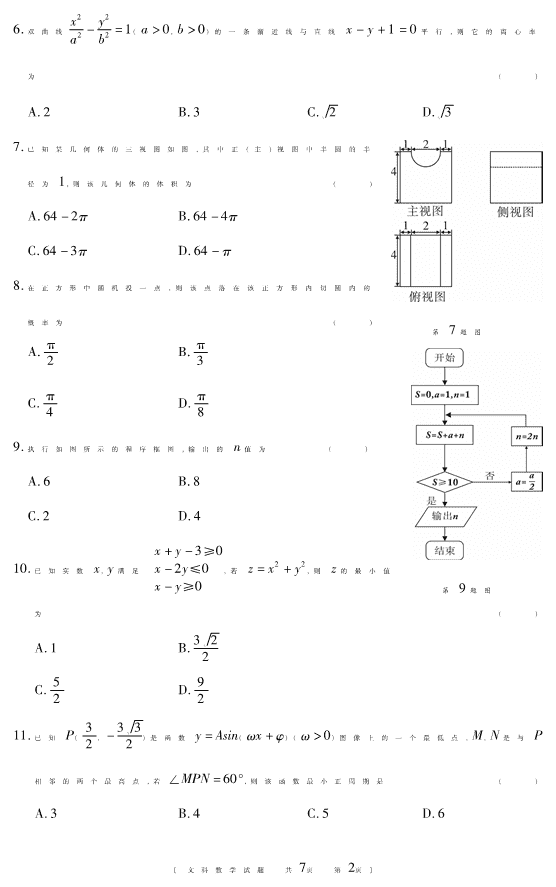
书书书 绝密★启用前 姓名 准考 证号 试卷类型:A 2018年咸阳市高考模拟考试试题(二) 文科数学 注意事项: 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分 150分.考试时间 120分钟. 2.答题前,考生务必将自己的姓名、准考证号填写在本试题及答题卡相应的位置. 3.全部答案在答题卡上完成,答在本试题上无效. 4.考试结束后,将本试题和答题卡一并交回. 第Ⅰ卷 一、选择题 :本大题共 12小题,每小题 5分,共 60分,在每小题给出的四个选项中,只有 一项符合题目要求. 1.集合 M={x|x≥ -2},N={x|1<x<2},则 M∩N= ( ) A.{x|-2≤x<2} B.{x|x≥ -2} C.{x|x<2} D.{x|1<x<2} 2.设复数 z=1+i 1-i(i为虚数单位),z的共轭复数为 z- ,则|z- |= ( ) A.1 B.0 C.2 D.1 2 3.函数 f(x)=2x-1 x零点的个数为 ( ) A.0 B.1 C.2 D.3 4.设向量 a→ 和 b→ 满足:|a→ +b→ 槡|=2 3,|a→ -b→ |=2,则 a→·b→ = ( ) 槡 槡A.2 B.3 C.2 D.3 5.圆(x-1)2+(y-1)2=2关于直线 y=kx+3对称,则 k的值是 ( ) A.2 B.-2 C.1 D.-1 〕页1第 页7共 题试学数科文〔 6.双曲线x2 a2 -y2 b2 =1(a>0,b>0)的一条渐近线与直线 x-y+1=0平行,则它的离心率 为 ( ) 槡 槡A.2 B.3 C.2 D.3 第 7题图 7.已知某几何体的三视图如图,其中正(主)视图中半圆的半 径为 1,则该几何体的体积为 ( ) A.64-2π B.64-4π C.64-3π D.64-π 8.在正方形中随机投一点,则该点落在该正方形内切圆内的 概率为 ( ) 第 9题图 A.π 2 B.π 3 C.π 4 D.π 8 9.执行如图所示的程序框图,输出的 n值为 ( ) A.6 B.8 C.2 D.4 10.已知实数 x,y满足 x+y-3≥0 x-2y≤0 x-y≥{ 0 ,若 z=x2 +y2,则 z的最小值 为 ( ) A.1 B. 槡3 2 2 C.5 2 D.9 2 11.已知 P(3 2,- 槡3 3 2 )是函数 y=Asin(ωx+φ)(ω>0)图像上的一个最低点,M,N是与 P 相邻的两个最高点,若∠MPN=60°,则该函数最小正周期是 ( ) A.3 B.4 C.5 D.6 〕页2第 页7共 题试学数科文〔 12.已知定义在 R上的函数 f(x)的导函数为 f′(x),且 f(x)+f′(x)>1,设 a=f(2)-1, b=e[f(3)-1],则 a,b的大小关系为 ( ) A.a<b B.a>b C.a=b D.无法确定 第Ⅱ卷 本卷包括必考题和选考题两个部分.第 13题 ~第 21题为必考题,每个试题考生都必 须作答.第 22题、第 23题为选考题,考生根据要求作答. 二、填空题 :本大题共 4小题,每小题 5分,共 20分,把答案填写在答题卡的相应位置. 13.平面直角坐标系中,角 α的顶点在原点,始边与 x轴非负半轴重合,终边过点 P(-5,-12),则 cosα= . 14.下表是某工厂 1~4月份用水量(单位:百吨): 月份 x 1 2 3 4 用水量 y 5.5 4 3.5 3 由散点图可知,用水量 y与月份 x之间有较好的线性相关关系,其线性回归方程 y=-0.4x+b,则 b= . 15.已知函数 f(x)= log2(3-x),x<2 2x-2,x≥{ 2 ,则 f(log212)+f(1)= . 16.一个正三棱锥的所有棱长均为槡2,则它的外接球的表面积为 . 三、解答题 :本大题共 6小题,共 70分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分 12分) 已知数列{an}的前 n项和为 Sn,且 Sn=2an-1(n∈N ). (Ⅰ)求 a1,a2,a3; (Ⅱ)求数列{an}的通项公式. 〕页3第 页7共 题试学数科文〔 18.(本小题满分 12分) 如图,在四棱锥 P-ABCD中,四边形 ABCD为正方形,PA⊥平面 ABCD,PA=AB,M是 PC上一点. (Ⅰ)若 BM⊥PC,求证:PC⊥平面 MBD; (Ⅱ)若 M为 PC的中点,且 AB=2,求三棱锥 M-BCD的 体积. 19.(本小题满分 12分) 针对国家提出的延迟退休方案,某机构进行了网上调查,所有参与调查的人中,持“支 持”、“保留”和“不支持”态度的人数如下表所示: 支持 保留 不支持 50岁以下 8000 4000 2000 50岁以上(含 50岁) 1000 2000 3000 (Ⅰ)在所有参与调查的人中,用分层抽样的方法抽取 n个人,已知从持“不支持”态度 的人中抽取了 30人,求 n的值; (Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取 5人看成一个总体,从这 5人 中任意选取 2人,求至少有一人年龄在 50岁以下的概率; (Ⅲ)在接受调查的人中,有 10人给这项活动打出的分数如下:9.4,8.6,9.2,9.6, 8.7,9.3,9.0,8.2,8.3,9.7,把这 10个人打出的分数看作一个总体,从中任取一个数, 求该数与总体平均数之差的绝对值超过 0.6概率. 〕页4第 页7共 题试学数科文〔 20.(本小题满分 12分) 已知 A(-2,0),B(2,0),点 C是动点,且直线 AC和直线 BC的斜率之积为 -3 4. (Ⅰ)求动点 C的轨迹方程; (Ⅱ)设直线 l与(Ⅰ)中轨迹相切于点 P,与直线 x=4相交于点 Q,且 F(1,0) 求证:∠PFQ=90°. 21.(本小题满分 12分) 已知函数 f(x)=x2 a-2lnx(a∈R,a≠0). (Ⅰ)讨论 f(x)的单调性; (Ⅱ)若函数 f(x)有最小值,记为 g(a),关于 a的方程 g(a)+a-2 9a-1=m有三个不 同的实数根,求实数 m的取值范围. 〕页5第 页7共 题试学数科文〔 请考生在第 22、23题中任选一题做答,如果多做,则按所做的第一题计分,做答时请 写清题号. 22.(本小题满分 10分)选修 4-4:坐标系与参数方程 在平面直角坐标系 xOy中,曲线 C的方程是:(x-5)2 +y2 =10,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系. (Ⅰ)求曲线 C的极坐标方程; (Ⅱ)设过原点的直线 l与曲线 C交于 A,B两点,且|AB|=2,求直线 l的斜率. 〕页6第 页7共 题试学数科文〔 23.(本小题满分 10分)选修 4-5:不等式选讲 已知函数 f(x)=|x|-|x-3|(x∈R) (Ⅰ)求 f(x)的最大值 m; (Ⅱ)设 a,b,c∈R+,且 2a+3b+4c=m,求证:1 2a+1 3b+1 4c≥3. 〕页7第 页7共 题试学数科文〔查看更多