2020届二轮复习命题的概念与真假判断学案(全国通用)
命题的概念与真假判断
· 命题的概念
一般地,用语言、符号或式子表达的可以判断真假的陈述句叫做命题(proposition).判断一个语句是不是命题,就要看它是否符合“是陈述句”和“可以判断真假”这两个条件.一个命题一般可以用一个小写英文字母来表示,如 p,q,r,⋯.
· 真命题与假命题
判断为真的命题称为真命题(true proposition);判断为假的命题称为假命题(false proposition).
精选例题
命题的概念与真假判断
1. 已知 p: 方程 x2-mx+1=0 有两个不相等的正实数根;q: 方程 4x2+4m-2x+m2=0 无实数根.若“ p 或 q ”为真,“ p 且 q ”为假.则下列结论:
① p,q 都为真;
② p,q 都为假;
③ p,q 一真一假;
④ p,q 至少有一个为真;
⑤ p,q 至多有一个为假.
其中正确结论的序号是 .实数 m 的取值范围是 .
【答案】 ③;m<-2 或 m>1
2. 给出下列四个命题:①梯形的对角线一定相等;② 对任意实数 x,均有 x+2>x;③不存在实数 x,使 x2+x+1<0;④有些三角形不是等腰三角形.其中所有正确命题的序号为 .
【答案】 ②③④
3. 判断下列语句是否为命题,并把结果填在句末的横线上:
(1)空间内垂直于同一条直线的两条直线一定平行. (2)等边三角形难道不是等腰三角形吗? (3)x∈2,+∞. (4)若 x>1,则 x>2.
【答案】 (1)是;(2)不是;(3)不是;(4)是
4. 有下列四个命题:
①“若 x+y=0,则 x,y 互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若 q⩽1,则 x2+2x+q=0 有实根”的逆否命题;
④“不等边三角形的三个内角相等”的逆命题.
其中真命题的序号为 .
【答案】 ①③
5. 判断下列语句是否为命题,并把结果填在句末的横线上:
(1)难道 2 不是正数? (2)当 0
0.
【答案】 (1)不是;(2)是
6. 下列四种说法:
①函数 y=x2-x+4x-1 x>1 的最小值为 5;
②等差数列 an 中,a1,a3,a4 成等比数列,则公比为 12;
③已知 a>0,b>0,a+b=1,则 23+3b 的最小值为 5+26;
④方程 x2+ax+2b=0 的两个实数根为 x1,x2,且 01 时,x-1>0,
所以 y=x2-x+4x-1=x-1+4x-1+1⩾2x-1⋅4x-1+1=5,故①正确;
等差数列 an 中,a1,a3,a4 成等比数列,
则 a32=a1⋅a4,即 a1+2d2=a1⋅a1+3d,
解得:a1=-4d,或 d=0,
则公比为 12 或 1,
故②错误;
a>0,b>0,a+b=1,则 2a+3b=2a+3ba+b=2ba+3ab+5⩾5+26;
故③正确;
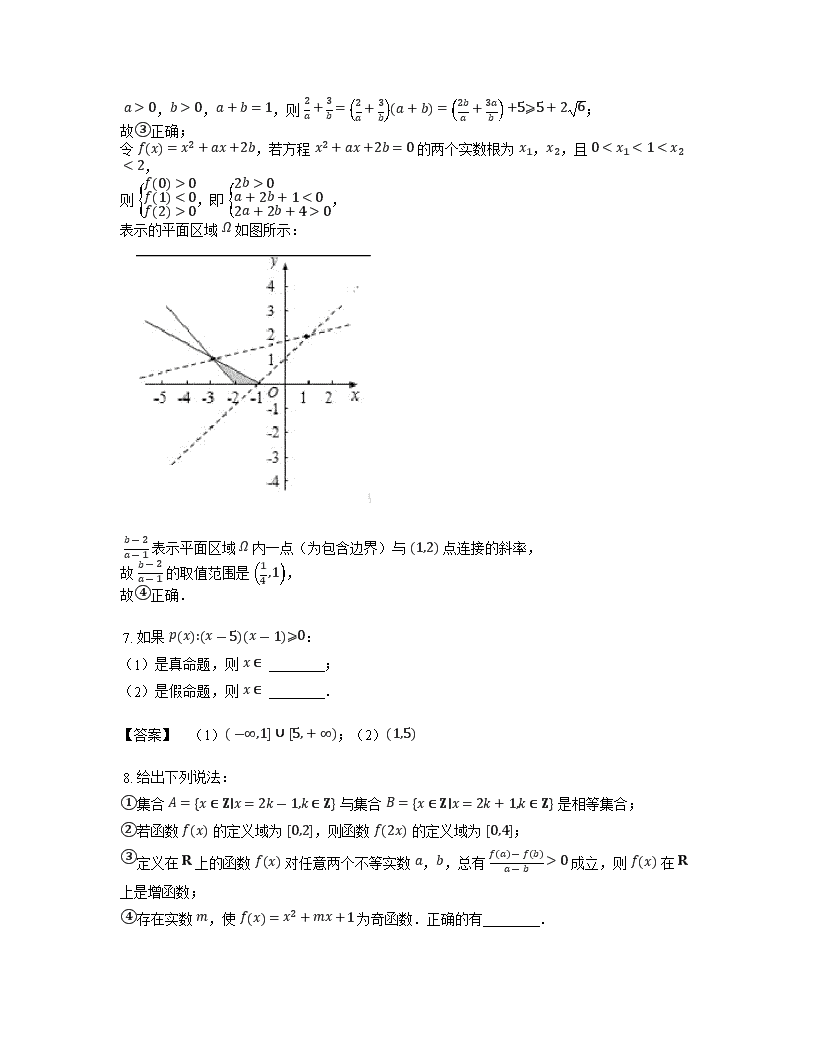
令 fx=x2+ax+2b,若方程 x2+ax+2b=0 的两个实数根为 x1,x2,且 00f1<0f2>0,即 2b>0a+2b+1<02a+2b+4>0,
表示的平面区域 Ω 如图所示:
b-2a-1 表示平面区域 Ω 内一点(为包含边界)与 1,2 点连接的斜率,
故 b-2a-1 的取值范围是 14,1,
故④正确.
7. 如果 px:x-5x-1⩾0:
(1)是真命题,则 x∈ ;
(2)是假命题,则 x∈ .
【答案】 (1)-∞,1∪5,+∞;(2)1,5
8. 给出下列说法:
①集合 A=x∈Zx=2k-1,k∈Z 与集合 B=x∈Zx=2k+1,k∈Z 是相等集合;
②若函数 fx 的定义域为 0,2,则函数 f2x 的定义域为 0,4;
③定义在 R 上的函数 fx 对任意两个不等实数 a,b,总有 fa-fba-b>0 成立,则 fx 在 R 上是增函数;
④存在实数 m,使 fx=x2+mx+1 为奇函数.正确的有 .
【答案】 ①③
9. 判断下列命题的真假,并把结果填在句末的横线上:
(1)0⩾0. (2)0 是空集. (3)∃x∈R,x>2. (4)∀x∈R,x>2.
【答案】 (1)真;(2)假;(3)真;(4)假
10. 下列命题:① ∀x∈R,x2+1>0;② ∀x∈N,x2⩾1;③ ∃x∈Z,x3<1;④ ∃x∈Q,x2=3;⑤ ∀x∈R,x2-3x+2=0;⑥ ∃x∈R,x2+1=0.其中所有真命题的序号是 .
【答案】 ①③
11. 判断下列存在性命题的真假:(1)∃x∈R,x⩽0 ;(2)至少有一个整数,它既不是合数,也不是素数 ;(3)∃x∈x∣x是无理数,x2 是无理数 .
【答案】 (1)真;(2)真;(3)真
12. ① ∀x∈R,2x2-x+1>0;②" x>1 且 y>2 "是" x+y>3 "的充要条件;③ 函数 y=x2+2+1x2+2 的最小值为 2
其中假命题的为 (将你认为是假命题的序号都填上)
【答案】 ②,③
【分析】 提示:
①,2x2-x+1 中 Δ=-7<0,所以 y=2x2-x+1 的图象都在 x 轴上方,所以 ∀x∈R,2x2-x+1>0;
②,当 x+y>3 时,有可能 x⩽1,所以②错;
③,因为 x2+2⩾2,所以利用均值定理时等号取不到.③错.
13. 有下列命题:
① y=cosx-π4cosx+π4 的图象关于直线 x=π2 对称;
② y=x+3x-1 的图象关于点 -1,1 对称;
③关于 x 的方程 ax2-2ax-1=0 有且仅有一个实根,则 a=-1;
④满足条件 AC=3,∠B=60∘,AB=1 的三角形 △ABC 有两个.
其中真命题的序号是 .
【答案】 ①③
【分析】 因为 cosx+π4=sinπ2-x+π4=-sinx-π4,所以 y=cosx-π4cosx+π4=12cos2x,所以函数的图象关于直线 x=π2 对称;函数 y=x+3x-1=1+4x-1,所以函数关于点 1,1 对称;方程 ax2-2ax-1=0 有且仅有一个实根时,满足 4a2+4a=0,当 a=0 不成立,所以 a=-1;由正弦定理得 3sin60∘=1sinC,解得 sinC=12,所以 C=30∘ 或 C=150∘(舍).
14. 下列说法中正确的有 .
①平均数不受少数几个极端值的影响,中位数受样本中的每一个数据影响;
②抛掷两次硬币,出现"两枚都是正面朝上"、"两枚都是反面朝上"、"恰好一枚硬币正面朝上"的概率一样大;
③用样本的频率分布估计总体分布的过程中,样本容量越大,估计越准确;
④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型.
【答案】 ③
15. 下列命题中,正确的是 .
① 在空间中,若四点不共面,则每三个点一定不共线;
② 若 Am,10,Bm+2,10,点 P 满足 ∣PA∣-∣PB∣=1,则点 P 的轨迹是双曲线;
③ 若点 Pm,n 到直线 l:x+1=0 的距离为 m-12+n2,则点 P 的轨迹为抛物线;
④ 正方体 ABCD-A1B1C1D1 的棱长为 1,O 是底面 A1B1C1D1 的中心,则 O 到平面 ABC1D1 的距离为 24.
【答案】 ①③④
16. 对于函数:① fx=lg∣x-2∣+1;② fx=x-22;③ fx=cosx+2.判断如下三个命题的真假:
命题甲:fx+2 是偶函数;
命题乙:fx 在 -∞,2 上是减函数,在 2,+∞ 上是增函数;
命题丙:fx+2-fx 在 -∞,+∞ 是增函数.
则能使命题甲、乙、丙均为真的函数序号是 .
【答案】 ②
17. 以下四个关于圆锥曲线的命题中
① 设 A 、 B 为两个定点, k 为非零常数, ∣PA∣-∣PB∣=k ,则动点 P 的轨迹为双曲线;
② 过定圆 C 上一定点 A 作圆的动弦 AB , O 为坐标原点,若 OP=12OA+OB, 则动点 P 的轨迹为椭圆;
③方程 2x2-5x+2=0 的两根可分别作为椭圆和双曲线的离心率;
④ 双曲线 x225-y29=1 与椭圆 x235+y2=1 有相同的焦点.
其中真命题的序号为 .(写出所有真命题的序号)
【答案】 ③④
【分析】 对于 ① :根据双曲线的定义 ,必须 ∣k∣<∣AB∣ 时,动点 P 的轨迹才是双曲线 ,则 ① 错 ;
对于 ② :因为 OP=12OA+OB, 所以 P 为弦 AB 的中点,从而 ∠APC=900 ,于是动点 P 的轨迹为以线段 AC 为直径的圆 ,故 ② 错 .
18. 命题“存在 x∈-1,1,2x+a=0 ”是真命题,则 a 的取值范围为 .
【答案】 -2,2
设 fx=2x+a,由题意得函数 fx 在 -1,1 内有零点,
所以 a+2a-2<0,
所以 -2x2; (2)x∈R,x+1⩽x+2.
【答案】 (1)假;(2)真
20. 下面是关于四棱柱的四个命题:
①若有两个侧面垂直于底面,则该四棱柱是直四棱柱;
②若四个过相对侧棱的截面都垂直于底面,则该四棱柱是直四棱柱;
③若四个侧面两两全等,则该四棱柱是直四棱柱;
④若四棱柱的四条对角线两两相等,则该四棱柱是直四棱柱.
其中,真命题的编号为 .
【答案】 ②④
【分析】 ①错,必须是两个相邻的侧面;
②正确;因两个过相对侧棱的截面都垂直于底面,可得到侧棱垂直于底面;
③错,反例,可以是斜四棱柱;
④正确,对角线两两相等,则此两对角线所在的平行四边形为矩形.
21. 如果 p:关于 x 的不等式 x2+2ax+4>0 对一切 x∈R 都成立,q:关于 x 的方程 4x2+4a-2x+1=0 无实数根,且 p 与 q 中有且只有一个是真命题,求实数 a 的取值范围.
【解】 当 p 为真时,由 Δ=2a2-4×4<0,
可得 -20,
所以 p 为真时,530,
所以 q 为真时,1-5,
所以 p:m>-5.
因为方程 2x+m=0 有实数根且 2x>0,
所以 m<0,
所以 q:m<0.
因为命题 p,q 中有且只有一个为真命题,
所以存在两种情况:
① 当 p 为真命题,q 为假命题时,
有 m>-5,m⩾0,
所以 m⩾0.
② 当 p 为假命题,q 为真命题时,
有 m⩽-5,m<0,
所以 m⩽-5.
所以 m 的取值范围是 -∞,-5∪0,+∞.
26. 已知命题 p:函数 fx=log2ax2-x+a16 的定义域为 R;q:不等式 2x+1<1+ax 对一切正实数 x 均成立.若 p 和 q 都是假命题,求实数 a 的取值范围.
【解】 当 p 为真时,有 ax2-x+a16>0,x∈R 成立,
所以 a>0,且 Δ=1-a24<0,
解得 a>2.
所以 p 为假时,a⩽2.
当 q 为真时,a>2x+1-1x 对一切正实数 x 均成立,
即 a>22x+1+1.
又因为 fx=22x+1+1 在 0,+∞ 上是减函数,
所以 fx1,则方程 x2-2x+m=0 无实数根;
⑦ 已知 a、b、c∈R,若 a≠c 或 b≠d,则 a+b≠c+d;
⑧已知 a、b、c∈R,若 a+b≠c+d,则 a≠c 或 b≠d.
【解】 ① 假命题,还可能是异面直线;
②假命题,这两个平面可以平行也可以相交,不一定垂直;
③假命题,常数函数是周期函数,但没有最小正周期;
④假命题,反例:2-1⋅2+1=2-1=1.
⑤ 假命题,反例:A=1,2,B=1,满足 A⊈B,且 A∩B=B;
⑥真命题,m>1 时,Δ=-22-4m<0,则方程 x2-2x+m=0 无实数根;
⑦假命题,如 a=1,b=3,c=d=2 即为反例;
⑧真命题,“已知 a、b、c∈R,若 a+b≠c+d,则 a≠c 或 b≠d ”的逆否命题为:若 a=c 且 b=d,则 a+b=c+d,为真命题,故原命题也为真命题.
28. 试判断命题“一次函数 fx=kx+bk≠0,若 m0,fn>0,则对任意 x⩽m,n 都有 fx>0 ”是真命题还是假命题,并说明理由.
【解】 真命题.因为一次函数是单调函数,m0,fn>0,所以 ∀x∈m,n,fx>0.
29. 设命题 p:a>1;命题 q: 不等式 -3x⩽a 对一切正实数均成立.
(1)若命题 q 为真命题,求实数 a 的取值范围;
【解】 当命题 q 为真命题时,由 x>0 得 3x>1,
所以 -3x<-1,
因为不等式 -3x⩽a 对一切正实数均成立,
所以 -1⩽a.
所以实数 a 取值范围是 -1,+∞
(2)命题“ p∨q ”为真命题,且“ p∧q ”为假命题,求实数 a 的取值范围.
【解】 由命题“ p∨q ”为真,且“ p∧q ”为假,得命题 p,q 一真一假.
① 当 p 真 q 假时,a>1,a,-1, 无解.
② 当 p 假 q 真时,a⩽1,a⩾-1,
所以 -1⩽a⩽1.
所以实数 a 的取值范围是 -1,1
30. 分别写出下列命题的逆命题、否命题、逆否命题,并判断其真假:
(1)若 q<1,则方程 x2+2x+q=0 有实根;
【解】 逆命题:若方程 x2+2x+q=0 有实根,则 q<1,为假命题,
否命题:若 q⩾1,则方程 x2+2x+q=0 无实根,假命题,
逆否命题:若方程 x2+2x+q=0 无实根,则 q⩾1,真命题;
(2)若 ab=0,则 a=0 或 b=0.
【解】 逆命题:若 a=0 或 b=0,则 ab=0,真命题,
否命题:若 ab≠0,则 a≠0 且 b≠0,真命题,
逆否命题:若 a≠0 且 b≠0,则 ab≠0,真命题.
31. 判断下列语句是否是命题:
(1)张三是四川人;
【解】 是命题;
(2) 10n 是个很大的数;
【解】 不是命题;
(3) x2+2x=0 ;
【解】 不是命题;
(4) x2+6>0 ;
【解】 不是命题;
(5) 1+1>2 ;
【解】 是命题.
32. 已知 a>0,设命题 p:函数 y=ax 在 R 上单调递减;命题 q:不等式 x+x-2a>1 的解集为 R.若 p 和 q 有且只有一个正确,求 a 的取值范围.
【解】 由函数 y=ax 在 R 上单调递减知 01 的解集为 R,即 y=x+x-2a 在 R 上恒大于 1.
又因为 x+x-2a=2x-2a,x⩾2a,2a,x<2a,
所以函数 y=x+x-2a 在 R 上的最小值为 2a.
故要使解集为 R,只需 2a>1,所以 a>12,即 q:a>12.
若 p 真 q 假,则 00,2m+8>0,2m+84.
则 q 为假命题时,m⩽-4或-2⩽m⩽4;p 为假命题时,m≥3.
所以 p∨q 是假命题,实数 m 的取值范围 3,4.
【解】 3,4.
36. 设有两个命题:
①"关于 x 的不等式 x2+a-1x+a2>0 的解集是 R ";
② "函数 fx=2a2+a+1x 是 R 上的减函数".
若命题①和②中至少有一个是真命题,求实数 a 的取值范围.
【解】 解设命题①为假,则 a-12-4a2⩾0⇔-1⩽a⩽13.
再设命题②为假,则 2a2+a+1⩽0 或 2a2+a+1⩾1⇔a⩽-12 或 a⩾0.
若①,②同时为假,则 -1⩽a⩽-12 或 0⩽a⩽13.
从而①,②中至少有一个为真时,a 的取值范围是 -∞,-1 或 -12,0 或 13,+∞.
37. 已知命题 p:ax2+2x+1>0,若对 ∀x∈R,p 是真命题,求实数 a 的取值范围.
【解】 由题意可得,∀x∈R,ax2+2x+1>0 恒成立.
(i)当 a=0 时,ax2+2x+1=2x+1>0,显然不恒成立,不合题意.
(ii)当 a≠0 时,要使 ax2+2x+1>0 恒成立,则
a>0,4-4a<0,
解得 a>1.
综上可知,所求实数 a 的取值范围是 1,+∞.
38. 已知点 Px0,y0 在曲线 fx,y=0 上,也在曲线 gx,y=0 上,求证:点 P 在曲线 fx,y+λgx,y=0 上(λ∈R).
【解】 ∵Px0,y0 在曲线 fx,y=0 上,
∴fx0,y0=0.
同理 gx0,y0=0,
∴fx0,y0+λgx0,y0=0+λ⋅0=0λ∈R,
即 Px0,y0 也在曲线 fx,y+λgx,y=0λ∈R 上.
39. 已知命题:"若 α=2kπ+βk∈Z,则 sinα=sinβ ",写出它的逆命题、否命题和逆否命题,并判断它们的真假.
【解】 逆命题:"若 sinα=sinβ,则 α=2kπ+βk∈Z ",假命题;
否命题:"若 α≠2kπ+βk∈Z,则 sinα≠sinβ ",假命题;
逆否命题:"若 sinα≠sinβ,则 α≠2kπ+βk∈Z ",真命题.
40. 判断下列命题的真假:
(1)中国所有的江河都流入太平洋;
【解】 真;
(2)有的四边形既是矩形,又是菱形;
【解】 真;
(3)实系数方程都有实数解;
【解】 假;
(4)有的数比它的倒数小.
【解】 真.
课后练习
1. 给出下列四个命题:
①命题“ ∀x∈R,x2⩾0 ”的否定是“ ∃x∈R,x2⩽0 ”;
②函数 y=fx 的定义域为 -∞,-1∪1,+∞,其图象上任一点 Px,y 满足 x2-y2=1,则函数 y=fx 可能是奇函数;
③若 a,b∈0,1,则不等式 a2+b2<14 成立的概率是 π4;
④函数 y=log2x2-ax+2 在 2,+∞ 上恒为正,则实数 a 的取值范围是 -∞,52.
其中真命题的序号是 .(请填上所有真命题的序号)
2. 有下列命题:
① 双曲线 x225-y29=1 与椭圆 x235+y2=1 有相同焦点;
② “ -12bc,则 a>b ”的逆命题;
④“若 a+5∈Q,则 a∈Q ”的逆命题.
正确的命题是 (请填入正确命题的序号).
4. 在 △ABC 中,三内角 A,B,C 的对边分别为 a,b,c.
命题 p: 若 a>acosB+bcosA,则 A>C.
命题 q: 若 A>B,则 sinA>sinB.
给出下列四个结论:
①命题 q 的逆命题、否命题、逆否命题都是真命题;
②命题“ p∧q ”是假命题;
③命题“ p∨¬p ”是假命题;
④命题“ ¬p∨¬q ”是假命题.
其中所有正确结论的序号是 .
5. 给出下列命题:
① y=1 是幂函数;
② 函数 fx=2x-log2x 的零点有 1 个;
③ x-1x-2⩾0 的解集为 2,+∞;
④ " x<1 "是" x<2 "的充分不必要条件;
⑤ 函数 y=x3 在点 O0,0 处切线是 x 轴.
其中真命题的序号是 (写出所有正确命题的编号)
6. 有下列四个命题:
①在 △ABC 中,a 、 b 分别是角 A 、 B 所对的边,若 ab,则 -1a>-1b;
③在正项等比数列 an 中,若 a4a5=9,则 log3a1+log3a2+⋯+log3a8=8;
④ 若关于 x 的不等式 mx2+mx+1>0 恒成立,则 m 的取值范围是 0,4.
其中所有正确命题的序号为 .
7. 给出如下四个命题,其中不正确的命题的个数是 .
①若" p 且 q "为假命题,则 p,q 均为假命题;
②命题"若 x⩾2 且 y⩾3,则 x+y⩾5 "的否命题为"若 x⩾2 且 y⩾3,则 x+y<5 ";
③四个实数 a,b,c,d 依次成等比数列的必要不充分条件是 ad=bc;
④在 △ABC 中," A>45∘ "是" sinA>22 "的充分不必要条件.
8. ① OC 是 ⊙O 的半径;② AB⊥OC;③直线 AB 切 ⊙O 于点 C.请以其中两个语句为条件,一个语句为结论,写出一个真命题 .
9. 下面给出的四个命题中:
①以抛物线 y2=4x 的焦点为圆心,且过坐标原点的圆的方程为 x-12+y2=1;
②若 m=-2,则直线 m+2x+my+1=0 与直线 m-2x+m+2y-3=0 相互垂直;
③命题“ ∃x∈R,使得 x2+3x+4=0 ”的否定是“ ∀x∈R,都有 x2+3x+4≠0 ”;
④将函数 y=sin2x 的图象向右平移 π3 个单位,得到函数 y=sin2x-π6 的图象.
其中是真命题的有 (将你认为正确的序号都填上).
10. 有下列命题:
①若 p∧q 为假命题,则 p 、 q 均为假命题;
② " x=1 "是" x2-3x+2=0 "的充分不必要条件;
③命题"若 x2-3x+2=0,则 x=1 "的逆否命题为:"若 x≠1,则 x2-3x+2≠0 ";
④对于命题 p:∃x∈R,使得 x2+x+1<0,则 ¬p:∀x∈R,均有 x2+x+1⩾0.
其中所有正确结论的序号是 .
11. 下列说法中:
①命题:"存在 x∈R, 使得 x2+1>3x "的否定是"对任意 x∈R, 都有 x2+1⩽3x ".
②若直线 a 、 b 在平面 α 内的射影互相垂直,则 a⊥b.
③已知一组数据为 20 、 30 、 40 、 50 、 60 、 70,则这组数据的众数、中位数、平均数的大小关系是:众数 > 中位数 > 平均数.
④已知回归方程 y=4.4x+838.19,则可估计 x 与 y 的增长速度之比约为 522.
⑤若 A-2,3,B3,-2,C12,m 三点共线,则 m 的值为 2.
所有正确说法的序号是 .
12. 已知下列命题:
① AB+BC+CA=0;
②函数 y=fx-1 的图象向左平移 1 个单位后得到的函数图象解析式为 y=fx;
③函数 y=f1+x 的图象与函数 y=f1-x 的图象关于 y 轴对称;
④满足条件 AC=3,∠B=60∘,AB=1 的 △ABC 有两个.
其中正确命题的序号是 .
13. 命题①:关于 x 的不等式 a-2x2+2a-2x-4<0 对 x∈R 恒成立;命题②:fx=-1-3a-a2x 是减函数.若命题①、②至少有一个为真命题,则实数 a 的取值范围是 .
14. 给出下列命题:
①“若 k>0,则关于 x 的方程 x2+2x-k=0 有实根”的逆命题为 ;
②“若 a>b,则 2a>2b-1 ”的否命题为 ;
③“若 A∪B=B,则 A⊆B ”的逆否命题为 ;
④命题 p:“ x,y∈R,若 x2+y2=0,则 x,y 全为 0 ”的非命题为 .
你写出的命题是真命题的序号是 .
15. 给出下列命题:
①函数 y=tanx 的图象关于点 kπ,0 k∈Z 对称;
②若向量 a,b,c 满足 a⋅b=a⋅c 且 a≠0,则 b=c;
③把函数 y=3sin2x+π3 的图象向右平移 π6 得到 y=3sin2x 的图象;
④若数列 an 既是等差数列又是等比数列,则 an=an+1n∈N*.
其中不正确命题的序号为 .
16. 给出如下命题:
①命题“在 △ABC 中,若 A=B,则 sinA=sinB ”的逆命题为真命题;
②若动点 P 到两定点 F1-4,0,F24,0 的距离之和为 8,则动点 P 的轨迹为线段 F1F2;
③若 p∧q 为假命题,则 p,q 都是假命题;
④ 设 x∈R,则“ x2-3x>0 ”是“ x>4 ”的必要不充分条件.
⑤若实数 1,m,9 成等比数列,则圆锥曲线 x2m+y2=1 的离心率为 63;
其中所有正确命题的序号是 .
17. 举一个反例,说明命题“若 a,b 是无理数,则 a+b 是无理数”是假命题: .
18. 对于任意实数 a,b,c,下列命题:
①若 a>b,c≠0,则 ac>bc;②若 a>b,则 ac2>bc2;
③若 ac2>bc2,则 a>b;④若 a>b,则 1a<1b
中,真命题为 .
19. 给出下列四个命题:
①函数 y=tanx 的图象关于点 kπ+π2 ,0,k∈Z 对称;
②函数 fx=sin∣x∣ 是最小正周期为 π 的周期函数;
③设 θ 为第二象限的角,则 tanθ2>cosθ2,且 sinθ2>cosθ2;
④函数 y=cos2x+sinx 的最小值为 -1,
其中正确的命题是 .
20. 设有两个命题:①关于 x 的不等式 mx2+1>0 的解集是 R;②函数 fx=logmx 是减函数.如果这两个命题有且只有一个真命题,则实数 m 的取值范围是 .
21. 判断下列命题的真假:
(1)1⩽2;
(2)2⩽2;
(3)2⩽1.
22. 设命题 p: 函数 fx=lgax2-x+116a 的定义域为 R;命题 q: 不等式 2x+1<1+ax 对一切正实数 x 均成立.如果命题 p 或 q 为真命题,命题 p 且 q 为假命题,求实数 a 的取值范围.
23. 判断下列语句哪些是命题?如果是命题,是真命题还是假命题?
(1)末位数字是 0 的整数能被 5 整除;
(2)平行四边形的对角线相等且互相平分;
(3)两直线平行则斜率相等;
(4)在 △ABC 中,若 sinA=sinB,则 A=B;
(5)余弦函数是周期函数吗?
24. 写出命题"一组对边平行且相等的四边形是平行四边形"的逆命题,否命题,逆否命题,并且判断其真假.
25. 写出命题"若 a=b,则 a2=b2 "的逆命题、否命题和逆否命题,并判断它们的真假,说明理由.
26. 写出下列命题的逆命题,否命题,逆否命题,并判断它们的真假.
(1)"负数的平方是正数";
(2)"若 a 和 b 都是偶数,则 a+b 是偶数";
(3)"当 c>0 时,若 a>b,则 ac>bc ";
(4)"若 x+y=5,则 x=3 且 y=2 ".
27. 判断下列命题的真假:
(1)已知 a , b , c , d∈R ,若 a≠c ,或 b≠d ,则 a+b≠c+d ;
(2) ∀x∈N , x3>x2 ;
(3)若 m>1 ,则方程 x2-2x+m=0 无实数根;
(4)存在一个三角形没有外接圆.
28. 把下列命题改写成‘‘若 p 则 q ”的形式,并写出它们的逆命题、否命题与逆否命题,同时指出它们的真假:
(1)对顶角相等;
(2)四条边相等的四边形是正方形.
29. 已知命题 p: “若 ac⩾0,则二次方程 ax2+bx+c=0 没有实根”:
(1)写出命题 p 的否命题;
(2)判断命题 p 的否命题的真假,并证明你的结论.
30. 写出下列命题的逆命题、否命题与逆否命题,并分别判断它们的真假:
(1)若 x2=1,则 x=1;
(2)矩形的对角线相等.
31. 设命题 p:方程x21-2m+y2m+2=1 表示双曲线;命题 q:∃x0∈R,x02+2mx0+2-m=0.
(1)若命题 p 为真命题,求实数 m 的取值范围;
(2)若命题 q 为真命题,求实数 m 的取值范围;
(3)求使“ p∨q ”为假命题的实数 m 的取值范围.
32. 判断下列命题的真假:
(1)4⩾3;
(2)4⩾4;
(3)4⩾5.
33. 判断下列命题的真假.
(1)作用力与反作用力是一对大小相等、方向相反的向量;
(2)数轴是向量;
(3)温度是向量.
34. 判断下列说法是否正确:
(1)一个命题的否命题为真,它的逆命题也一定为真;
(2)一个命题的逆否命题为真,它的逆命题不一定为真.
35. 写出下列命题的逆命题、否命题与逆否命题,并分别判断它们的真假:
(1)若 a=b,则 a=b;
(2)若 x<0,则 x2>0.
36. 已知 p:函数 fx=lgax2-x+116a 的定义域为 R;q:不等式 a>1x+1 对一切正实数 x 均成立.如果" p 或 q "为真命题," p 且 q "为假命题,求实数 a 的取值范围.
命题的概念与真假判断-出门考
姓名 成绩
1. 给定下列命题:
① 若 k>0,则方程 x2+2x-k=0 有实数根;
② 若 a>b,则 a+c>b+c;
③ 对角线相等的四边形是矩形;
④ 若 xy=0,则 x,y 中至少有一个为 0.
其中真命题的序号是 .
2. 有下面四个判断:①命题"设 a,b∈R,若 a+b≠6,则 a≠3 或 b≠3 "是一个假命题;②若 " p 或 q "为真命题,则 p,q 均为真命题;③在 △ABC 中," A>30∘ "是" sinA>12 "的充分不必要条件;④设向量 a=sin2θ,cosθ,b=cosθ,1,则" a∥b "是" tanθ=12 "成立的必要不充分条件.其中所有错误的判断有 .(填序号)
3. 下列说法中:
①若正数 a,b 满足 1a+4b=2,则 ab 的最小值为 4;
②在平面上,到定点 2,-1 的距离与到直线 3x-4y-10=0 距离相等的点的轨迹是抛物线;
③双曲线 x216-y225=1 的渐近线的夹角正切是 -409;
④以球心为原点建立的空间直角坐标系中,若 A2,2,-1 、 B-1,2,2 为球面上两点,则过 A 、 B 的大球劣弧长(即 A 、 B 的球面距离)为 3π2.
其中正确命题的序号是 .
4. 给出下列命题:
①对数函数 y=log2a-5x 在 0,+∞ 是增函数,则实数 a 的取值范围是 3,+∞;
②若不等式 x-3+x+1>a 的解集为 R,则实数 a 的取值范围是 4,+∞;
③若方程 2ax2-x-1=0 在 0,1 内恰有一解,则实数 a 的取值范围是 1,+∞;
④在 △ABC 中,若 AB=1,BC=2,则角 C 的取值范围是 0,π6,其中真命题的编号是 (写出所有真命题的编号).
5. 给出下列命题:
① y=1 是幂函数;
② 函数 fx=2x-x2 的零点有 2 个;
③ x+1x+25 展开式的项数是 6 项;
④ 函数 y=sinxx∈-π,π 图象与 x 轴围成的图形的面积是 S=-ππsinxdx;
⑤若 ξ∼N1,σ2,且 P0⩽ξ⩽1=0.3,则 Pξ⩾2=0.2.
其中真命题的序号是 .(写出所有正确命题的编号)
6. 对 ∀x∈R,kx2-kx-1<0 是真命题,则 k 的取值范围是 .
7. 给出下列四个命题:
①函数 fx=3sin2x-π3 的图象关于点 -π6,0 对称;
②若 a⩾b>-1,则 a1+a⩾b1+b;
③存在实数 x,使 x3+x2+1=0;
④设 Px1,y1 为圆 O1:x2+y2=9 上任意一点,圆 O2:x-a2+y-b2=1,当 x1-a2+y1-b2=1 时,两圆相切.
其中正确命题的序号是 .(把你认为正确的都填上)
8. 以下命题:
①若 x≠1 或 y≠2,则 x+y≠3;
②若空间向量 OA,OB 与空间中任一向量都不能组成空间的一组基底,则 OA 与 OB 共线;
③若函数 y=fx 在 x=x0 处导数等于 0,则该函数在该点处取得极值;
④若 A,B 为两个定点,K 为正常数,若 ∣PA∣+∣PB∣=K,则动点 P 的轨迹是椭圆;
⑤已知抛物线 y2=2px,以过焦点的一条弦 AB 为直径作圆,则此圆与准线相切;
其中真命题为 .(写出所有真命题的序号)
9. 判断下列命题的真假:
(1)面积相等的三角形是全等三角形;
(2)若两平面平行,则其中一个平面内的直线平行于另一个平面;
(3)3 是无理数;
(4)5⩾7;
(5)若 xy=0,则 x=0 且 y=0;
(6)正方体均为正四棱柱.
10. 给出下列命题:
①当 sin2θ<0 时,θ 是第二、三象限角;
②直线 2x-3y-8=0 与圆 x-12+y+22=10 一定相交;
③函数 fx=x+1xx⩾2 的最小值是 2.
其中真命题的序号是 .
11. 给出下列四个命题:
①设 fx 是定义在 R 上的可导函数,fʹx 为函数 fx 的导函数,则 “ fʹx0=0 ” 是“ x0 为 fx 极值点”的必要不充分条件;
②双曲线 x2m2+12-y24-m2=1 的焦距与 m 有关;
③命题"中国人不都是北京人"的否定是"中国人都是北京人";
④命题" 若 ca-db>0,且 bc-ad<0,则 ab>0 ".
其中正确结论的序号是 .
12. 已知集合 A=x∣x2-3x+2⩽0,集合 B 为函数 y=x2-2x+a 的值域.命题 p:A∩B≠∅.若命题 p 为假命题,则实数 a 的取值范围是 .
13. 下列说法:
①已知 e 是单位向量,a+e=a-2e,则 a 在 e 方向上的投影为 12;
②关于 x 的不等式 ax>1 成立;
(2)已知椭圆 x25+y2m=1 的离心率 e=105,则 m 的值为 3;
(3)对于函数 fx=2x2+mx+n,若 fa>0,fb>0,则函数在 a , b 内至多有一个零点;
(4)函数 y=fx-2 与 y=f2-x 的图象关于直线 x=2 对称;
其中正确命题的序号是 .
17. 已知 a>0,函数 fx=ax2+bx+c,若 x0 满足关于 x 的方程 2ax+b=0,则下列四个命题:
① ∃x∈R,fx⩽fx0;
② ∃x∈R,fx⩾fx0;
③ ∀x∈R,fx⩽fx0;
④ ∀x∈R,fx⩾fx0.
其中假命题的序号是 .
18. 有下列命题:
①若 a>b,则 ac2>bc2;
②直线 x-y-1=0 的倾斜角为 45∘,纵截距为 -1;
③直线 l1:y=k1x+b1 与直线 l2:y=k2x+b2 平行的充要条件是 k1=k2 且 b1≠b2;
④当 x>0 且 x≠1 时,lgx+1lgx⩾2;
⑤到坐标轴距离相等的点的轨迹方程为 x-y=0.
其中真命题的是 .
19. 把下面不完整的命题补充完整,并使之成为真命题.若函数 fx=2+log3x 的图象与 gx 的图象关于 对称,则函数 gx= .
20. 给定两个命题,P:对任意实数 x 都有 ax2+ax+1>0 恒成立;Q:关于 x 的方程 x2-x+a=0 有实数根.如果 P 与 Q 中有且仅有一个为真命题,则实数 a 的取值范围为 .