- 2024-05-04 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
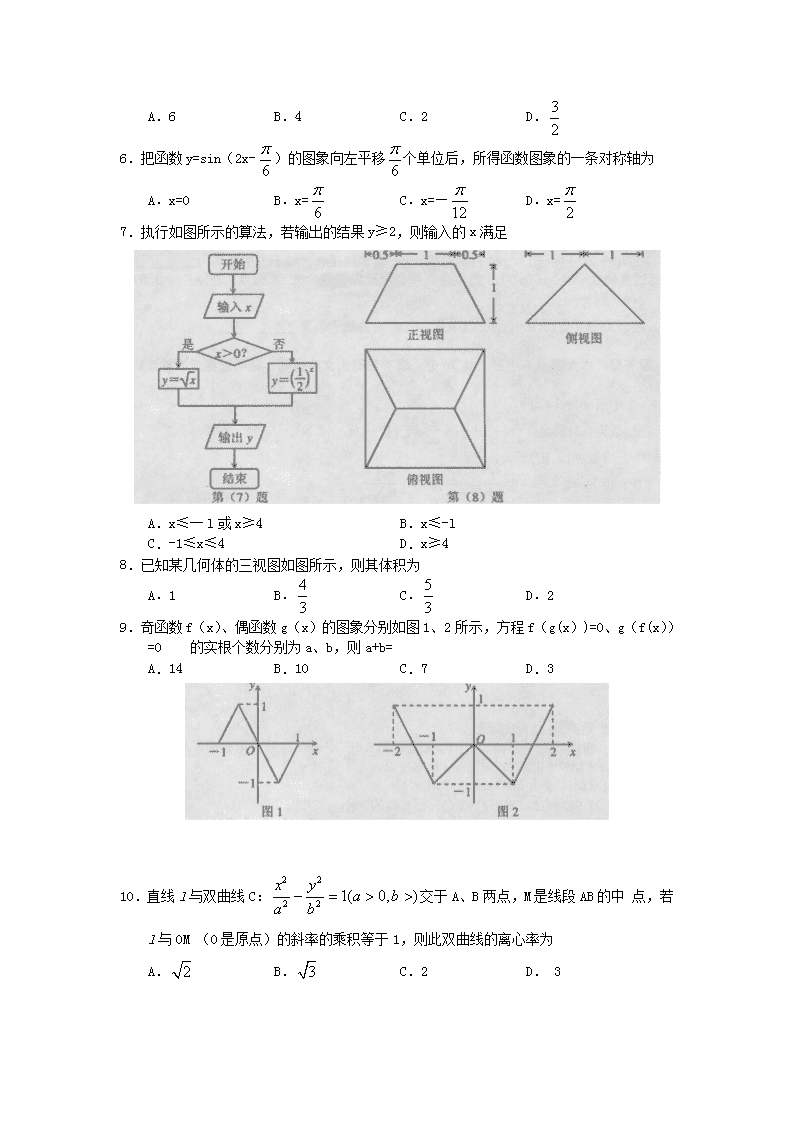
河北省唐山市2012届高三数学下学期第二次模拟考试试题 理 新人教A版
河北省唐山市2011—2012学年度高三年级第二次模拟考试 数学(理)试题 说明: 一、本试卷共4页,包括三道大题,24道小题,共150分,其中1.~(21)小题为必做题,(22)~(24)小题为选做题. 二、答题前请仔细阅读答题卡上的“注意事项”,按照“注意事项”的规定答题. 三、做选择题时,每小题选出答案后,用2B铅笔把答题卡上对应题目的标号涂黑.如需改动,用橡皮将原选涂答案擦干净后,再选涂其他答案, 四、考试结束后,将本试卷与原答题卡一并交回, 参考公式: 样本数据的标准差; 为样本平均数; 柱体体积公式:、h为高; 锥体体积公式:为高; 球的表面积、体积公式:其中R为球的半径。 一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项符合题目要求. 1.已知=2+i,则复数z的共轭复数为 A.-3-i B.-3+i C.3+i D.3-i 2.的展开式中的常数项为 A.-15 B.15 C.-20 D.20 3.己知命题p:“a>b”是“2a>2b”的充要条件;q:∈R,lx+l l≤x,则 A.pq为真命题 B.pq为假命题 C.pq为真命题 D. pq为真命题 4.已知是第三象限的角,且tan=2,则sin(+)= A. B. C. D. 5.设变量x、y满足则目标函数z=2x+y的最小值为 A.6 B.4 C.2 D. 6.把函数y=sin(2x-)的图象向左平移个单位后,所得函数图象的一条对称轴为 A.x=0 B.x= C.x=— D.x= 7.执行如图所示的算法,若输出的结果y≥2,则输入的x满足 A.x≤一l或x≥4 B.x≤-l C.-1≤x≤4 D.x≥4 8.已知某几何体的三视图如图所示,则其体积为 A.1 B. C. D.2 9.奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0 的实根个数分别为a、b,则a+b= A.14 B.10 C.7 D.3 10.直线l与双曲线C:交于A、B两点,M是线段AB的中 点,若l与OM (O是原点)的斜率的乘积等于1,则此双曲线的离心率为 A. B. C.2 D. 3 11.曲线y=与其在点(0,一1)处的切线及直线x=1所围成的封闭图形的面积为 A.1-ln2 B.2-2n2 C. ln2 D.2ln2-1 12.把一个皮球放入如图所示的由8根长均为20 cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都有接触点,则皮球的半径为 A.l0cm B.10 cm C.10cm D.30cm 二、填空题:本大题共4小题,每小题5分,共20分 13.函数y=的定义域为 。 14.向圆(x一2)2+(y—)=4内随机掷一点,则该点落在x轴下方的概率为 。 15.过抛物线y2=2px(p>0)的焦点F作直线交抛物线于A、B两点,若|AF| =2|BF|=6,则p= 。 16.在△ABC中,(则角A的最大值为 。 三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤 17.(本小题满分12分) 已知数列满足:. (I)求数列的通项公式; (II)设,求 18.(本小题满分12分) 某篮球队甲、乙两名队员在本赛零已结束的8场比赛中得分统计的茎叶图如下: (I)比较这两名队员在比赛中得分的均值和方差的大小; (II)以上述数据统计甲、乙两名队员得分超过15分的频率作为概率,假设甲、乙两名队员在同一场比赛中得分多少互不影响,预测在本赛季剩余的2场比赛中甲、乙两名队员得分均超过15分次数X的分布列和均值. 19.(本小题满分12分) 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB= 2AD =2CD =2.E是PB的中点. (I)求证:平面EAC⊥平面PBC; (II)若二面角P-A C-E的余弦值为,求直线PA与平面EAC所成角的正弦值. 20.(本小题满分12分) 在直角坐标系xOy中,长为的线段的两端点C、D分别在x轴、y轴上滑动,.记点P的轨迹为曲线E. (I)求曲线E的方程; ( II)经过点(0,1)作直线l与曲线E相交于A、B两点,当点M在曲线E上时,求的值. 21.(本小题满分12分) 已知. (I)求函数f(x)的最小值; ( II)(i)设 (ii)若,且证明: 请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑. 22.(本小题满分10分)选修4-1:几何证明选讲 如图,在△ABC中,BC边上的点D满足BD=2DC,以BD为直径作圆O恰与CA相切于点A,过点B作BE⊥CA于点E,BE交圆D于点F. (I)求∠ABC的度数: ( II)求证:BD=4EF. 23.(本小题满分10分)选修4-4:坐标系与参数方程 极坐标系的极点为直角坐标系xOy的原点,极轴为z轴的正半轴,两种坐标系的长度单位相同,己知圆C1的极坐标方程为p=4(cos+sin,P是C1上一动点,点Q在射线OP上且满足OQ=OP,点Q的轨迹为C2。 (I)求曲线C2的极坐标方程,并化为直角坐标方程; ( II)已知直线l的参数方程为(t为参数,0≤<),l与曲线C2有且只有一个公共点,求的值. 24.(本小题满分10分)选修4-5:不等式选讲 设f(x)=|x|+2|x-a|(a>0). (I)当a=l时,解不等式f(x)≤4; ( II)若f(x)≥4恒成立,求实数a的取值范围 唐山市2011—2012学年度高三年级第二次模拟考试 理科数学参考答案 一、 选择题: A卷:AABCB CDDCB CB B卷:CBDAC BACBA DB 二、填空题: (13)(lg2,+∞) (14)- (15)4 (16) 三、解答题: (17)解: (Ⅰ)=(32-1)=3, …1分 当n≥2时, ∵=(++…+)-(++…+) =(32n-1)-(32n-2-1)=32n-1, …5分 当n=1,=32n-1也成立, 所以an=. …6分 (Ⅱ)bn=log3=-(2n-1), …7分 ==(-), ∴++…+=[(1-)+(-)+…+(-)] …10分 =(1-)=. …12分 (18)解: (Ⅰ)甲=(7+9+11+13+13+16+23+28)=15, 乙=(7+8+10+15+17+19+21+23)=15, s=[(-8)2+(-6)2+(-4)2+(-2)2+(-2)2+12+82+132]=44.75, s=[(-8)2+(-7)2+(-5)2+02+22+42+62+82]=32.25. 甲、乙两名队员的得分均值相等;甲的方差较大(乙的方差较小). …4分 (Ⅱ)根据统计结果,在一场比赛中,甲、乙得分超过15分的概率分别为p1=,p2=,两人得分均超过15分的概率分别为p1p2=, 依题意,X~B(2,),P(X=k)=C()k()2-k,k=0,1,2, …7分 X的分布列为 X 0 1 2 P …10分 X的均值E(X)=2×=. …12分 (19)解: (Ⅰ)∵PC⊥平面ABCD,ACÌ平面ABCD,∴AC⊥PC, ∵AB=2,AD=CD=2,∴AC=BC=, ∴AC2+BC2=AB2,∴AC⊥BC, 又BC∩PC=C,∴AC⊥平面PBC, ∵ACÌ平面EAC,∴平面EAC⊥平面PBC. …4分 D A C E P B x y z (Ⅱ)如图,以C为原点,、、分别为x轴、y轴、z轴正向,建立空间直角坐标系,则C(0,0,0),A(1,1,0),B(1,-1,0). 设P(0,0,a)(a>0), 则E(,-,), …6分 =(1,1,0),=(0,0,a), =(,-,), 取m=(1,-1,0),则 m·=m·=0,m为面PAC的法向量. 设n=(x,y,z)为面EAC的法向量,则n·=n·=0, 即取x=a,y=-a,z=-2,则n=(a,-a,-2), 依题意,|cosám,nñ|===,则a=2. …10分 于是n=(2,-2,-2),=(1,1,-2). 设直线PA与平面EAC所成角为θ, 则sinθ=|cosá,nñ|==, 即直线PA与平面EAC所成角的正弦值为. …12分 (20)解: (Ⅰ)设C(m,0),D(0,n),P(x,y). 由=,得(x-m,y)=(-x,n-y), ∴得 …2分 由||=+1,得m2+n2=(+1)2, ∴(+1)2x2+y2=(+1)2, 整理,得曲线E的方程为x2+=1. …5分 (Ⅱ)设A(x1,y1),B(x2,y2),由=+,知点M坐标为(x1+x2,y1+y2). 设直线l的方程为y=kx+1,代入曲线E方程,得(k2+2)x2+2kx-1=0, 则x1+x2=-,x1x2=-. …7分 y1+y2=k(x1+x2)+2=, 由点M在曲线E上,知(x1+x2)2+=1, 即+=1,解得k2=2. …9分 这时x1x2+y1y2=x1x2+(kx1+1)(kx2+1)=(1+k2)x1x2+k(x2+x2)+1=-, (x+y)(x+y)=(2-x)(2-x)=4-2(x+x)+(x1x2)2 =4-2[(x1+x2)2-2x1x2]+(x1x2)2=, cosá,ñ==-. …12分 (21)解: (Ⅰ)f¢(x)=x-=. …1分 当x∈(0,a)时,f¢(x)<0,f(x)单调递减; 当x∈(a,+∞)时,f¢(x)>0,f(x)单调递增. 当x=a时,f(x)取得极小值也是最小值f(a)=a2-a2lna. …4分 (Ⅱ)(ⅰ)设g(t)=f(a+t)-f(a-t),则 当0<t<a时, g¢(t)=f¢(a+t)+f¢(a-t)=a+t-+a-t-=<0, …6分 所以g(t)在(0,a)单调递减,g(t)<g(0)=0,即f(a+t)-f(a-t)<0, 故f(a+t)<f(a-t). …8分 (ⅱ)由(Ⅰ),f(x)在(0,a)单调递减,在(a,+∞)单调递增, 不失一般性,设0<x1<a<x2, 因0<a-x1<a,则由(ⅰ),得 f(2a-x1)=f(a+(a-x1))<f(a-(a-x1))=f(x1)=f(x2), …11分 又2a-x1,x2∈(a,+∞), 故2a-x1<x2,即x1+x2>2a. …12分 (22)解: (Ⅰ)连结OA、AD. ∵AC是圆O的切线,OA=OB, ∴OA⊥AC,∠OAB=∠OBA=∠DAC, …2分 又AD是Rt△OAC斜边上的中线, C A B E D O F ∴AD=OD=DC=OA, ∴△AOD是等边三角形,∴∠AOD=60°, 故∠ABC=∠AOD=30°. …5分 (Ⅱ)由(Ⅰ)可知, 在Rt△AEB中,∠EAB=∠ADB=60°, ∴EA=AB=×BD=BD, EB=AB=×BD=BD, …7分 由切割线定理,得EA2=EF×EB, ∴BD2=EF×BD, ∴BD=4EF. …10分 (23)解: (Ⅰ)设点P、Q的极坐标分别为(ρ0,θ)、(ρ,θ),则 ρ=ρ0=·4(cosθ+sinθ)=2(cosθ+sinθ), 点Q轨迹C2的极坐标方程为ρ=2(cosθ+sinθ), …3分 两边同乘以ρ,得ρ2=2(ρcosθ+ρsinθ), C2的直角坐标方程为x2+y2=2x+2y,即(x-1)2+(y-1)2=2. …5分 (Ⅱ)将l的代入曲线C2的直角坐标方程,得 (tcosφ+1)2+(tsinφ-1)2=2,即t2+2(cosφ-sinφ)t=0, …7分 t1=0,t2=sinφ-cosφ, 由直线l与曲线C2有且只有一个公共点,得sinφ-cosφ=0, 因为0≤φ<p,所以φ=. …10分 (24)解: (Ⅰ)f(x)=|x|+2|x-1|= …2分 当x<0时,由2-3x≤4,得-≤x<0; 当0≤x≤1时,1≤2-x≤2; 当x>1时,由3x-2≤4,得1<x≤2. 综上,不等式f(x)≤4的解集为[-,2]. …5分 (Ⅱ)f(x)=|x|+2|x-a|= …7分 可见,f(x)在(-∞,a]单调递减,在(a,+∞)单调递增. 当x=a时,f(x)取最小值a. 所以,a取值范围为[4,+∞). …10分查看更多