- 2024-04-05 发布 |
- 37.5 KB |
- 3页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年八年级数学下册20微专题教材P154数学活动—中点四边形习题(新版)冀教版
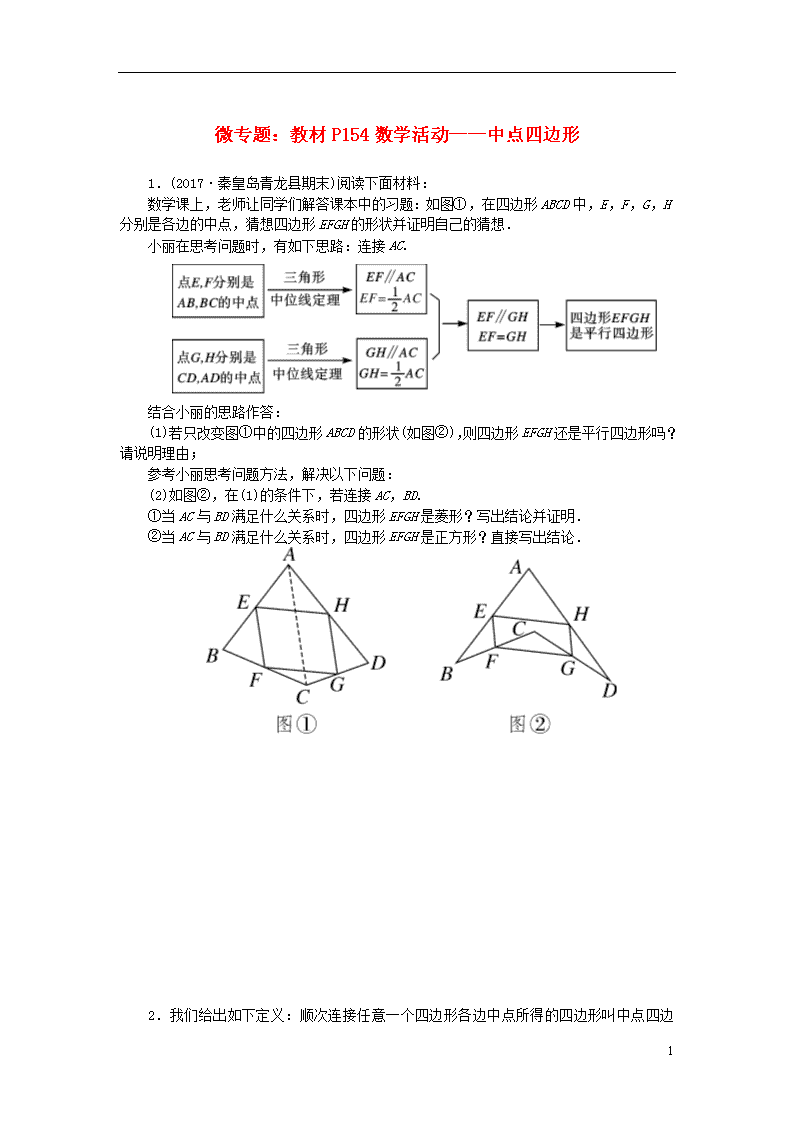
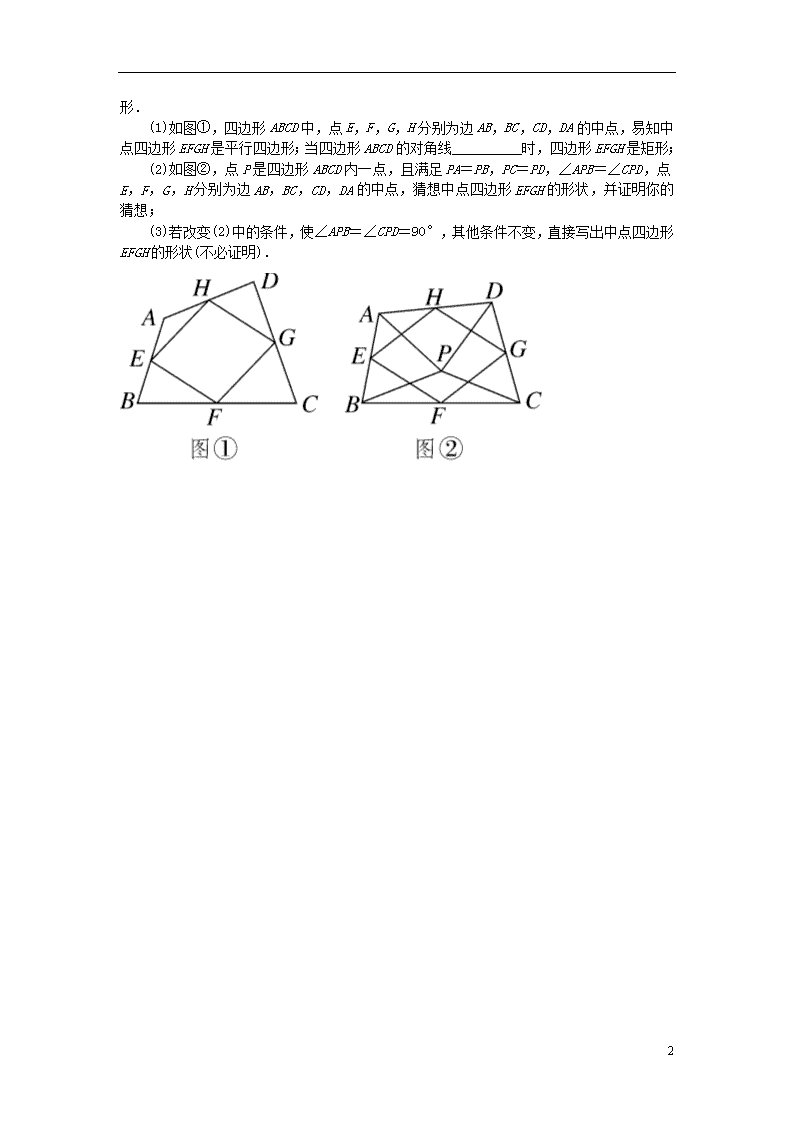
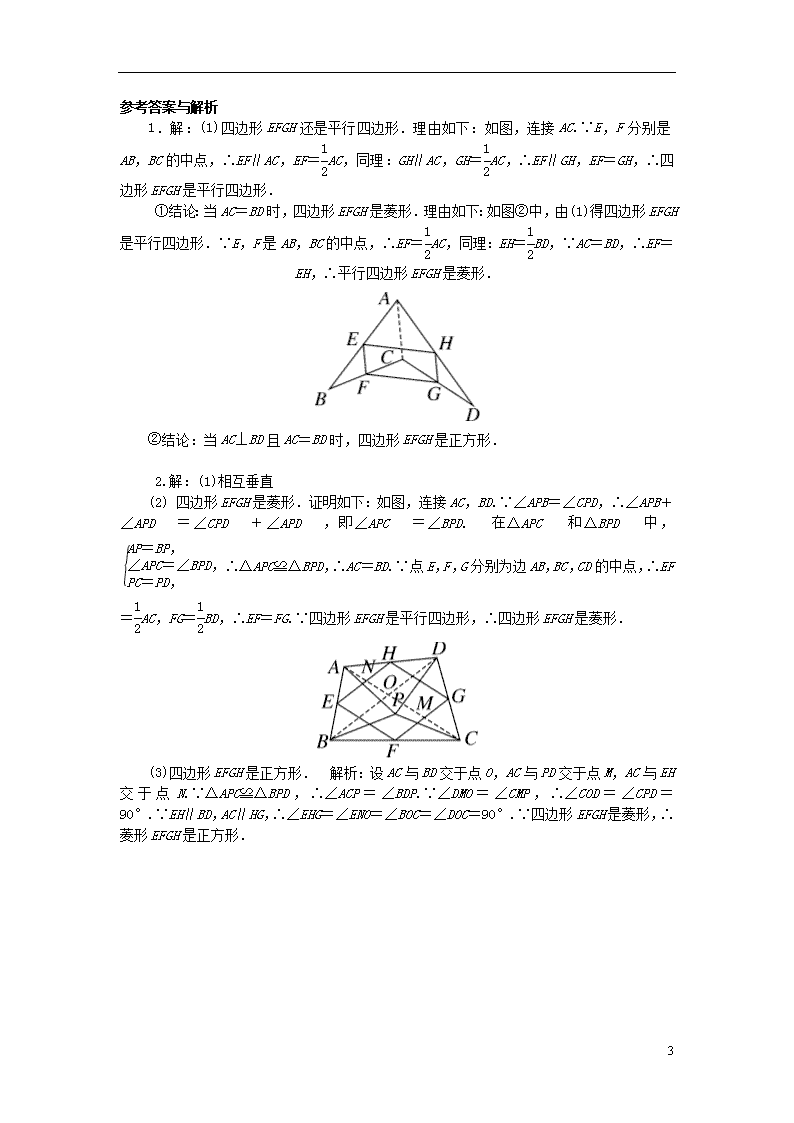
微专题:教材P154数学活动——中点四边形 1.(2017·秦皇岛青龙县期末)阅读下面材料: 数学课上,老师让同学们解答课本中的习题:如图①,在四边形ABCD中,E,F,G,H分别是各边的中点,猜想四边形EFGH的形状并证明自己的猜想. 小丽在思考问题时,有如下思路:连接AC. 结合小丽的思路作答: (1)若只改变图①中的四边形ABCD的形状(如图②),则四边形EFGH还是平行四边形吗?请说明理由; 参考小丽思考问题方法,解决以下问题: (2)如图②,在(1)的条件下,若连接AC,BD. ①当AC与BD满足什么关系时,四边形EFGH是菱形?写出结论并证明. ②当AC与BD满足什么关系时,四边形EFGH是正方形?直接写出结论. 3 2.我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形. (1)如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点,易知中点四边形EFGH是平行四边形;当四边形ABCD的对角线__________时,四边形EFGH是矩形; (2)如图②,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想; (3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状(不必证明). 3 参考答案与解析 1.解:(1)四边形EFGH还是平行四边形.理由如下:如图,连接AC.∵E,F分别是AB,BC的中点,∴EF∥AC,EF=AC,同理:GH∥AC,GH=AC,∴EF∥GH,EF=GH,∴四边形EFGH是平行四边形. ①结论:当AC=BD时,四边形EFGH是菱形.理由如下:如图②中,由(1)得四边形EFGH是平行四边形.∵E,F是AB,BC的中点,∴EF=AC,同理:EH=BD,∵AC=BD,∴EF=EH,∴平行四边形EFGH是菱形. ②结论:当AC⊥BD且AC=BD时,四边形EFGH是正方形. 2.解:(1)相互垂直 (2) 四边形EFGH是菱形.证明如下:如图,连接AC,BD.∵∠APB=∠CPD,∴∠APB+∠APD=∠CPD+∠APD,即∠APC=∠BPD.在△APC和△BPD中,∴△APC≌△BPD,∴AC=BD.∵点E,F,G分别为边AB,BC,CD的中点,∴EF=AC,FG=BD,∴EF=FG.∵四边形EFGH是平行四边形,∴四边形EFGH是菱形. (3)四边形EFGH是正方形. 解析:设AC与BD交于点O,AC与PD交于点M,AC与EH交于点N.∵△APC≌△BPD,∴∠ACP=∠BDP.∵∠DMO=∠CMP,∴∠COD=∠CPD=90°.∵EH∥BD,AC∥HG,∴∠EHG=∠ENO=∠BOC=∠DOC=90°.∵四边形EFGH是菱形,∴菱形EFGH是正方形. 3查看更多