高中数学必修2教案2_示范教案（3_1_2 两条直线平行与垂直的判定）

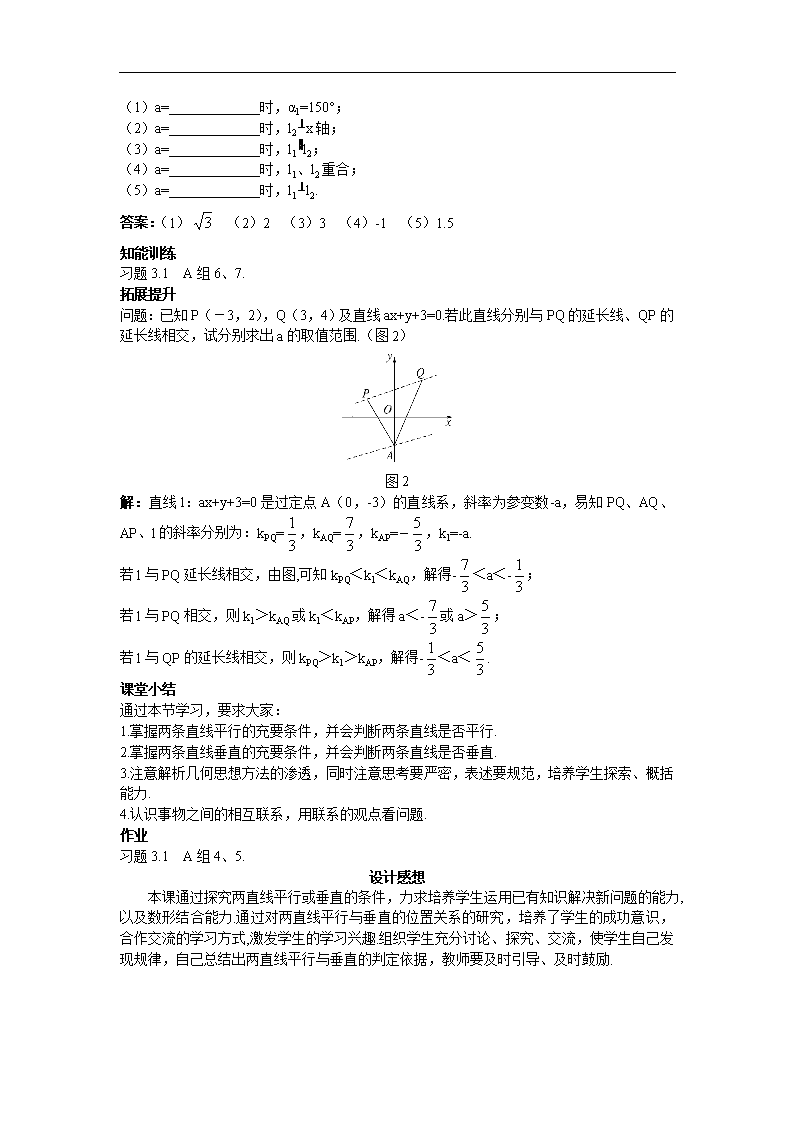
高中数学必修2教案2_示范教案（3_1_2 两条直线平行与垂直的判定）

‎3.1.2 两条直线平行与垂直的判定 整体设计 教学分析 ‎ 直线的平行和垂直是两条直线的重要位置关系，它们的判定，又都是由相应的斜率之间的关系来确定的，并且研究讨论的手段和方法也相类似，因此，在教学时采用对比方法，以便弄清平行与垂直之间的联系与区别.值得注意的是，当两条直线中有一条不存在斜率时，容易得到两条直线垂直的充要条件，这也值得略加说明.‎ 三维目标 ‎1.掌握两条直线平行的充要条件，并会判断两条直线是否平行.掌握两条直线垂直的充要条件，并会判断两条直线是否垂直.培养和提高学生联系、对应、转化等辩证思维能力.‎ ‎2.通过教学，提倡学生用旧知识解决新问题，注意解析几何思想方法的渗透，同时注意思考要严密，表述要规范，培养学生探索、概括能力.‎ 重点难点 教学重点:掌握两条直线平行、垂直的充要条件，并会判断两条直线是否平行、垂直.‎ 教学难点:是斜率不存在时两直线垂直情况的讨论（公式适用的前提条件）.‎ 课时安排 ‎1课时 教学过程 导入新课 思路1.设问（1)平面内不重合的两条直线的位置关系有哪几种？(2)两条直线的倾斜角相等，这两条直线是否平行？反过来是否成立？(3)“α=β”是“tanα=tanβ”的什么条件？根据倾斜角和斜率的关系,能否利用斜率来判定两条直线平行呢?‎ 思路2.上节课我们学习的是什么知识？想一想倾斜角具备什么条件时两条直线会平行、垂直呢?你认为能否用斜率来判断.这节课我们就来专门来研究这个问题.‎ 推进新课 新知探究 提出问题 ‎①平面内不重合的两条直线的位置关系有几种？‎ ‎②两条直线的倾斜角相等，这两条直线是否平行？反过来是否成立？‎ ‎③“α=β”是“tanα=tanβ”的什么条件？‎ ‎④两条直线的斜率相等，这两条直线是否平行？反过来是否成立？‎ ‎⑤l1∥l2时，k1与k2满足什么关系？‎ ‎⑥l1⊥l2时，k1与k2满足什么关系？‎ 活动:①教师引导得出平面内不重合的两条直线的位置关系有平行和相交，其中垂直是相交的特例.‎ ‎②数形结合容易得出结论.‎ ‎③注意到倾斜角是90°的直线没有斜率,即tan90°不存在.‎ ‎④注意到倾斜角是90°的直线没有斜率.‎ ‎⑤必要性：如果l1∥l2，如图1所示，它们的倾斜角相等,即α1=α2，tanα1=tanα2,即k1=k2.‎ 图1‎ 充分性：如果k1=k2,即tanα1=tanα2,‎ ‎∵0°≤α1＜180°，0°≤α2＜180°，∴α1=α2.于是l1∥l2.‎ ‎⑥学生讨论，采取类比方法得出两条直线垂直的充要条件.‎ 讨论结果：①平面内不重合的两条直线的位置关系有平行和相交，其中垂直是相交的特例.‎ ‎②两条直线的倾斜角相等，这两条直线平行，反过来成立.‎ ‎③“α=β”是“tanα=tanβ”的充要条件.‎ ‎④两条直线的斜率相等，这两条直线平行，反过来成立.‎ ‎⑤l1∥l2k1=k2.‎ ‎⑥l1⊥l2k1k2=-1.‎ 应用示例 例1 已知A（2，3），B（－4，0），P（－3，１），Q（－1，2），判断直线BA与PＱ的位置关系，并证明你的结论.‎ 解:直线BA的斜率kBA==0.5,‎ 直线PQ的斜率kPQ==0.5,‎ 因为kBA=kPQ.所以直线BA∥PQ.‎ 变式训练 ‎ 若A(-2,3),B(3,-2),C(,m)三点共线，则m的值为( )‎ A. B.- C.-2 D.2‎ 分析：kAB=kBC,,m=.‎ 答案：A 例2 已知四边形ABCD的四个顶点分别为A（0，0），B（2，-1），C(4,2),D(2,3),试判断四边形ABCD的形状，并给出证明.‎ 解：AB边所在直线的斜率kAB=-,‎ CD边所在直线的斜率kCD=-,‎ BC边所在直线的斜率kBC=,‎ DA边所在直线的斜率kDA=.‎ 因为kAB=kCD,kBC=kDA,所以AB∥CD,BC∥DA.‎ 因此四边形ABCD是平行四边形.‎ 变式训练 ‎ 直线l1：ax+3y+1=0，l2：x+(a-2)y+a=0，它们的倾斜角及斜率依次分别为α1，α2，k1，k2.‎ ‎（1）a=_____________时，α1=150°；‎ ‎（2）a=_____________时，l2⊥x轴；‎ ‎（3）a=_____________时，l1∥l2；‎ ‎（4）a=_____________时，l1、l2重合；‎ ‎（5）a=_____________时，l1⊥l2.‎ 答案：（1） （2）2 （3）3 （4）-1 （5）1.5‎ 知能训练 习题3.1 A组6、7.‎ 拓展提升 问题：已知P（－3，2），Q（3，4）及直线ax+y+3=0.若此直线分别与PQ的延长线、QP的延长线相交，试分别求出a的取值范围.（图2）‎ 图2‎ 解：直线l：ax+y+3=0是过定点A（0，-3）的直线系，斜率为参变数-a，易知PQ、AQ、AP、l的斜率分别为：kPQ=，kAQ=，kAP=，k1=-a.‎ 若l与PQ延长线相交，由图,可知kPQ＜k1＜kAQ，解得-＜a＜-；‎ 若l与PQ相交，则k1＞kAQ或k1＜kAP，解得a＜-或a＞；‎ 若l与QP的延长线相交，则kPQ＞k1＞kAP，解得-＜a＜.‎ 课堂小结 通过本节学习，要求大家：‎ ‎1.掌握两条直线平行的充要条件，并会判断两条直线是否平行.‎ ‎2.掌握两条直线垂直的充要条件，并会判断两条直线是否垂直.‎ ‎3.注意解析几何思想方法的渗透，同时注意思考要严密，表述要规范，培养学生探索、概括能力.‎ ‎4.认识事物之间的相互联系，用联系的观点看问题.‎ 作业 习题3.1 A组4、5.‎ 设计感想 ‎ 本课通过探究两直线平行或垂直的条件，力求培养学生运用已有知识解决新问题的能力,以及数形结合能力.通过对两直线平行与垂直的位置关系的研究，培养了学生的成功意识，合作交流的学习方式,激发学生的学习兴趣.组织学生充分讨论、探究、交流，使学生自己发现规律，自己总结出两直线平行与垂直的判定依据，教师要及时引导、及时鼓励.‎