2021届课标版高考文科数学大一轮复习课件：§2-2 函数的基本性质（讲解部分）

2021届课标版高考文科数学大一轮复习课件：§2-2 函数的基本性质（讲解部分）

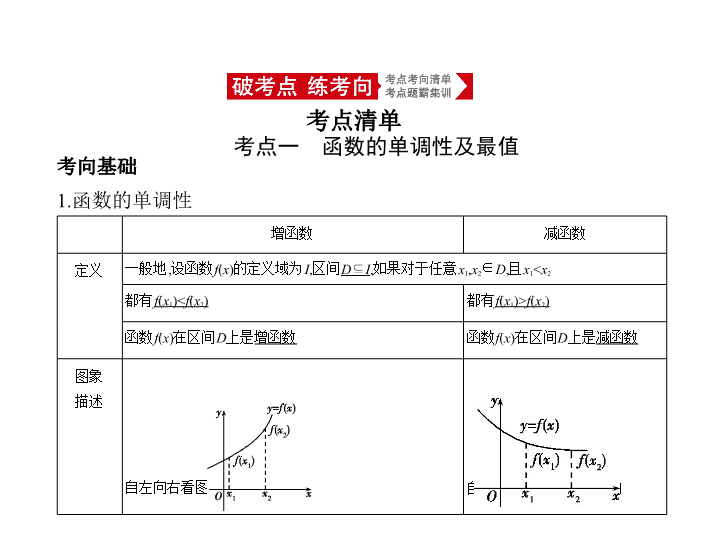
考点一　函数的单调性及最值 考点清单 考向基础 1.函数的单调性 增函数 减函数 定义 一般地,设函数 f ( x )的定义域为 I ,区间 D ⊆ I ,如果对于任意 x 1 , x 2 ∈ D ,且 x 1 < x 2 都有 f ( x 1 )< f ( x 2 ) 都有 f ( x 1 )> f ( x 2 ) 函数 f ( x )在区间 D 上是 增函数 函数 f ( x )在区间 D 上是 减函数 图象 描述   自左向右看图象是 上升 的   自左向右看图象是 下降 的 注意:(1)单调函数的定义有以下两种等价形式: ∀ x 1 , x 2 ∈[ a , b ],且 x 1 ≠ x 2 , ①   >0 ⇔ f ( x )在[ a , b ]上是增函数;   <0 ⇔ f ( x )在[ a , b ]上是减函数. ②( x 1 - x 2 )[ f ( x 1 )- f ( x 2 )]>0 ⇔ f ( x )在[ a , b ]上是增函数; ( x 1 - x 2 )[ f ( x 1 )- f ( x 2 )]<0 ⇔ f ( x )在[ a , b ]上是减函数. (2)单调区间只能用区间表示,当一个函数的增区间(或减区间)有多个时, 不 能用“ ∪ ”连接,而应该用“和”或“,”连接 .例如: y =   的单调减区间为 (- ∞ ,0)和(0,+ ∞ ),但不能写成(- ∞ ,0) ∪ (0,+ ∞ ). 2.函数的最值 前提 一般地,设函数 y = f ( x )的定义域为 I ,如果存在实数 M 满足 条件 对于任意的 x ∈ I ,都有 f ( x ) ≤ M ; 存在 x 0 ∈ I ,使得 f ( x 0 )= M 对于任意的 x ∈ I ,都有 f ( x ) ≥ M ; 存在 x 0 ∈ I ,使得 f ( x 0 )= M 结论 M 是 f ( x )的 最大 值 M 是 f ( x )的 最小 值 考向突破 考向一　求单调区间 例1    (2017课标全国Ⅱ,8,5分)函数 f ( x )=ln( x 2 -2 x -8)的单调递增区间是   (    　) A.(- ∞ ,-2)　    B.(- ∞ ,1) C.(1,+ ∞ )　    D.(4,+ ∞ ) 解析　本题主要考查复合函数的单调性. 由 x 2 -2 x -8>0可得 x >4或 x <-2, 所以 x ∈(- ∞ ,-2) ∪ (4,+ ∞ ), 令 u = x 2 -2 x -8, 则其在 x ∈(- ∞ ,-2)上单调递减, 在 x ∈(4,+ ∞ )上单调递增. 又因为 y =ln u 在 u ∈(0,+ ∞ )上单调递增, 所以 y =ln( x 2 -2 x -8)在 x ∈(4,+ ∞ )上单调递增.故选D. 答案    D   方法总结    复合函数的单调性符合同增异减的原则. 例2　(1)(2019河南郑州第一次质量预测,8)设函数 f ( x )=2ln( x +   )+3 x 3 (-2< x <2),则使得 f (2 x )+ f (4 x -3)>0成立的 x 的取值范围是   (　　) A.(-1,1)　     B.   　     C.   　     D.   (2)已知 f ( x )是定义在(0,+ ∞ )上的函数,对任意两个不相等的正数 x 1 , x 2 ,都有   >0,记 a =   , b =   , c =   ,则   (　　) A. a < b < c 　    B. b < a < c 　    C. c < a < b 　    D. c < b < a 考向二　单调性的应用 解析　(1)由题意知 f ( x )的定义域关于原点对称. f (- x )=2ln(- x +   )-3 x 3 =- f ( x ),所以 f ( x )为奇函数, 当 x ∈(0,2)时,易知函数 f ( x )=2ln( x +   )+3 x 3 是增函数, ∴函数 f ( x )在(-2,2)上是增函数. 不等式 f (2 x )+ f (4 x -3)>0可转化为 f (2 x )> f (3-4 x ),由函数 f ( x )在(-2,2)上是增函数 得   解得   < x <1,故选B. (2)∵ f ( x )是定义在(0,+ ∞ )上的函数,对任意两个不相等的正数 x 1 , x 2 ,都有   >0, ∴ x 1 - x 2 与 x 2 f ( x 1 )- x 1 f ( x 2 )同号, 则 x 1 - x 2 与     同号, ∴函数 y =   是(0,+ ∞ )上的增函数, ∵1<3 0.2 <2,0<0.3 2 <1,log 2 5>2,∴0.3 2 <3 0.2 0,则 f ( x )在R上为增函数,符合题意; 对于D,易知 f ( x )=ln(   - x )的定义域为R, f (- x )=ln(   + x )=-ln(   - x )=- f ( x ),则 f ( x )为奇函数, 设 t =   - x =   ,易知 t 在R上为减函数,而 y =ln t 为增函数,则 f ( x )= ln (   - x ) 在R上为减函数,不符合题意.故选C. 答案    C 方法2 　判断函数奇偶性的方法 1.定义法     3.性质法 若 f ( x ), g ( x )在其公共定义域上具有奇偶性,则奇+奇=奇,奇 × 奇=偶,偶+偶= 偶,偶 × 偶=偶,奇 × 偶=奇. 2.图象法 例2　判断下列函数的奇偶性: (1) f ( x )=(1- x )   ; (2) f ( x )=   (3) f ( x )=   ; (4) f ( x )=log 2 ( x +   ).   解析　(1)当且仅当   ≥ 0且1- x ≠ 0时函数有意义, ∴-1 ≤ x <1, ∴ f ( x )的定义域为[-1,1). ∵定义域关于原点不对称,∴函数 f ( x )是非奇非偶函数. (2)易知函数 f ( x )的定义域为{ x | x ≠ 0},关于原点对称, 当 x >0时,- x <0, f (- x )= x 2 -2 x -1=- f ( x ); 当 x <0时,- x >0, f (- x )=- x 2 -2 x +1=- f ( x ), ∴ f (- x )=- f ( x ),∴函数 f ( x )是奇函数. (3)由题意知   解得-2 ≤ x ≤ 2且 x ≠ 0, ∴函数 f ( x )的定义域为[-2,0) ∪ (0,2],关于原点对称. ∴ f ( x )=   =   , 又 f (- x )=   =-   =- f ( x ), ∴ f (- x )=- f ( x ),∴函数 f ( x )是奇函数. (4)解法一:易知 f ( x )的定义域为R. ∵ f (- x )=log 2 [(- x )+   ]=log 2   =-log 2 ( x +   )=- f ( x ),∴ f ( x )是奇函数. 解法二:易知 f ( x )的定义域为R. ∵ f (- x )+ f ( x )=log 2 [(- x )+   ]+log 2 ( x +   )=log 2 1=0,∴ f (- x )=- f ( x ), ∴ f ( x )为奇函数. 规律总结    (1)对于解析式比较复杂的函数,有时需要将函数化简后再判 断它的奇偶性,但一定要先考虑它的定义域; (2)对于分段函数,必须分段判断它的奇偶性,只有在每一段上都满足奇(偶) 函数的定义时,才能下相应的结论; (3)当 f ( x ) ≠ 0时,奇偶函数定义中的判断式 f (- x )= ± f ( x )常被它的变式   = ± 1 所替代. 方法3 　函数性质的综合应用的解题方法 求解函数性质的综合问题时,一要紧扣奇偶性、单调性、周期性的定义及 有关结论,二要充分利用各种性质之间的联系. 例3    (2019福建泉州质检,11)定义在R上的奇函数 f ( x )满足 f ( x +2)= f (- x ),且当 x ∈[0,1]时, f ( x )=2 x -cos x ,则下列结论正确的是   (　　) A. f   < f   < f (2 018) B. f (2 018)< f   < f   C. f (2 018)< f   < f   D. f   < f   < f (2 018) 解析　∵ f ( x )是奇函数,∴ f (- x )=- f ( x ), ∴ f ( x +2)= f (- x )=- f ( x ), ∴ f ( x +4)=- f ( x +2)= f ( x ), ∴ f ( x )的周期为4, ∴ f (2 018)= f (2+4 × 504)= f (2)= f (0), f   = f   , f   = f   , ∵ x ∈[0,1]时, f ( x )=2 x -cos x 单调递增, ∴ f (0)< f   < f   , ∴ f (2 018)< f   < f   ,故选C. 答案    C