- 2024-02-28 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中物理1.4 速度变化快慢的描述——加速度
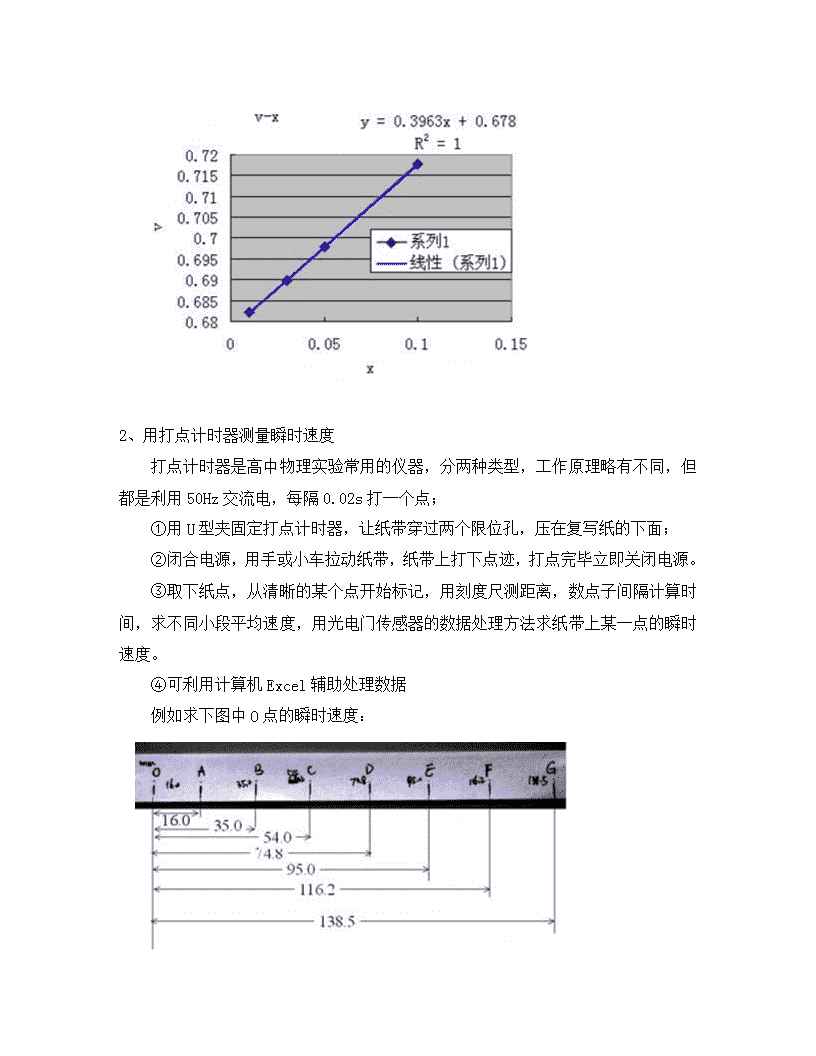
1.4 速度变化快慢的描述——加速度 主要内容 1、实验:瞬时速度的测量 2、加速度的概念 3、加速度的正负与加速运动、减速运动的关系 内容讲解 一、学生实验:瞬时速度的测量 1、用光电门传感器测瞬时速度 光电门传感器 滑块与挡光片 ①将光电门传感器固定在轨道一侧,连接到数据采集器第一通道。 ②打开数字化实验系统,设置挡光片为U型,点击“开始记录”。 ③依次将四种挡光片固定在滑块上,让滑块从轨道上同一位置滑下,记录下四次挡光时间后,点击“停止” ④打开“计算表格”,点击“变量”,添加挡光片宽度Δx,点击“公式”,选择“手动输入”,计算平均速度。 ⑤观察可见,随着Δx或时间值的减小,速度越来越趋近于某个定值,该定值即为滑块通过光电门时的瞬时速度。 ⑥点击“绘图”,选取X轴表示挡光片宽度Δx(或挡光片挡光时间Δt),Y轴为平均速度,点击“拟合”,选取合适类型,直接可得到图线方程,由方程可直接求出Δx(或Δt)趋近于零时的瞬时速度。 如下图: 也可以把上述数据导入Excel进行处理,处理方法同⑥,如下图: 2、用打点计时器测量瞬时速度 打点计时器是高中物理实验常用的仪器,分两种类型,工作原理略有不同,但都是利用50Hz交流电,每隔0.02s打一个点; ①用U型夹固定打点计时器,让纸带穿过两个限位孔,压在复写纸的下面; ②闭合电源,用手或小车拉动纸带,纸带上打下点迹,打点完毕立即关闭电源。 ③取下纸点,从清晰的某个点开始标记,用刻度尺测距离,数点子间隔计算时间,求不同小段平均速度,用光电门传感器的数据处理方法求纸带上某一点的瞬时速度。 ④可利用计算机Excel辅助处理数据 例如求下图中O点的瞬时速度: 从上面的数据也可以看出,对打点间隔为0.02s的这条纸点,相邻的一些点之间运动情况大致相同,如果不要求很精确,我们求下图中4点的瞬时速度,可用3到7之间的平均速度粗略代表。 当然,如果用3到5之间的平均速度代表4点的瞬时速度,就会更准确些。用这种方法,可简略地求出以上各点的瞬时速度。可设置如下表格记录数据。 若以0点作为计时起点,在上表中记录下各标记点所对应的时刻,以速度v为纵轴,时间t为横轴在方格纸上建立直角坐标,以上表中(v,t)为数据,在坐标系中描点,可得到另一种直观反映物理规律的图象,称为速度-时间图象(简称v-t图)。 上图为用手拉动纸带所得到的速度-时间图象,反映了用手拉动纸带时,速度随时间变化时大时小。 3、速度-时间图象 速度-时间图象表示物体运动的速度和时间的关系,在v-t图中很容易读出某一时刻所对应的速度,或某一速度所对应的时刻。 图线平行t轴表示匀速直线运动,速度的正负表示方向,①②为运动方向相反的两个匀速直线运动。 一条倾斜向上的直线表示正方向速度均匀增加的直线运动(v-t图中③) 一条倾斜向下的直线表示正方向速度均匀减小的直线运动(v-t图中④) 二、加速度的概念 观看豹子捕捉羚羊、导弹打飞机的视频。 思考:运动的快慢我们使用“速度”这个物理量来描述。在上面的视频中,这种生死的较量,比拼的不仅仅是速度,还要看“灵活”和“机动性好”,那么,灵活、机动性好该用什么物理量来描述呢? 观看视频:汽车、摩托车、飞机比赛。 思考:为什么飞机最终能领先?又为什么,一开始是摩托车遥远领先呢? 回答:飞机最终能领先是因为飞机的速度大;一开始摩托车领先,是因为摩托车速度变化的快。 1、变化量和变化率 就像位置变化快慢用速度来描述,速度的变化快慢也要用一个量来描述。那么,普遍的,一个量的变化快慢,我们都是怎么描述的呢?首先,变化量的定义是:变化量=末量—初量,描述该量的变化大小多少。变化快慢还要看变化量与时间的关系。因为,如果变化的很慢,但是持续时间很长,仍能够使最终变化量很大。这就好像是水滴石穿一样,虽然每滴水使石头发生的变化很小,但是持续很多年,甚至上千年后,积累的效果就会很显著。那么,衡量石头发生变化的快慢,就需要拿石头的变化量除以发生这些变化所用的时间,这个比值称为变化率。 变化率= ,描述该量的变化与时间的关系,即变化的快慢。 回顾速度的定义,速度是描述位置变化快慢的物理量。 位置 位置变化量 位置变化快慢——位置变化率 X △X(位移) △X/△t=速度 对比,可以得到速度的变化率: 速度 速度变化量 速度变化快慢 V △V △V/△t 2、加速度 我们称上述得到的表示速度变化快慢的物理量为加速度。表达式是a=,国际单位制中,由于速度的单位是m/s,所以加速度的单位是m/s2。 1:根据加速度的概念进行判断: A 点火后即将升空的火箭,由于它还没动,所以此时加速度是0。 错误。加速度表示的是速度变化的快慢,是物体速度变化的一种状态。刚点火的火箭就要升空,下一瞬间它的速度一定不为0,所以它的速度变化是不为0的,也就是它的加速度不为0。不要认为速度为0,加速度就为0,这两者是没有关系的。 B 轿车急刹车,速度变化很快,所以加速度很大。 正确。 C 高速运行的磁悬浮列车,速度很大,所以加速度很大。 错误。速度大小与加速度大小是没有关系的,速度很大的物体,做匀速运动时,速度不随时间变化,所以加速度为0。 D 空间站绕地球匀速转动,加速度不为0。 正确。速度是矢量,是有方向的。所以速度即使大小不变,只有方向改变,速度也是发生了改变的,所以也一定是有加速度的。 加速度是矢量。我们知道位移是矢量,速度v=,由于时间没有空间上的方向,所以速度也是有方向的,并且方向与位移Δx方向相同。同样的,由于加速度a的定义式是a=,我们可以得到加速度也是矢量,并且方向与速度的变化量Δv相同。 【注意】区别加速度的方向和速度的方向,加速度的方向与初速度、末速度的方向没有任何关系;但是,加速度的方向与速度变化量△V的方向总是一致的。 2:火车和汽车的比拼:谁的加速度大? 马自达6从静止加速至100km/h用10s 普通火车20秒钟达到4m/s。 答案:马自达6的加速度大小是2.8 m/s2,普通火车的加速度大小是0.2 m/s2,可见马自达6的机动性比火车好。但是请注意,加速度大并不表示速度大,最终还是火车会跑的比马自达6快一些。 体会:灵活、机动性好为何用加速度描述最好;联想老鹰捉小鸡的游戏。 思考:“加速度”这个概念是人类到了牛顿时代才建立起来的,那些古希腊的先哲们穷尽毕生也没能建立起加速度的概念。因为生活中,对于运动的物体可以问它走了多远,这是路程或者位移的概念;可以问它走的多快,这是速度的概念,已经比较抽象了。然而在生活中,没有准确的词汇与加速度对应。可以说,不学物理,在头脑中是不会自发的形成加速度的概念的。 有人说:“加速度很好理解啊。你看我开车,一挂高档,一踩油门,时速表就从20变到40,这不就是说明加速度很大吗?”其实,他是搞混了速度变化量与速度变化率(加速度)的区别。如果他说,一挂高档,一踩油门,忽的一下,时速表就从20变到40,这倒也表达了一种对加速度的朴素的认识。因为“忽的一下”说明他考虑到了时间在其中的作用。 区别:速度大、速度变化量大、速度变化快的不同,各自用什么量来描述。 三、加速度的正负与加速运动、减速运动的关系 火车启动、汽车进站,一个做加速运动,一个做减速运动。我们来看一下它们各自的加速度怎么样?因为加速度是矢量,我们先规定向右为正方向。 直线运动 t(s) 0 1 2 3 火车v(m/s) 5.0 5.3 5.6 5.9 汽车v(m/s) 30 25 20 15 计算结果:火车加速度是0.3 m/s2,汽车加速度是-5 m/s2。 汽车加速度的负号表示方向与正方向相反。 火车做加速运动,计算出的加速度为正;汽车做减速运动,计算出的加速度为负,是否说明“加速度为正,物体做加速运动;加速度为负,物体做减速运动”呢? 我们改变正反向再计算一次。这时它们的速度各自变成如下表: 直线运动t(s) 0 1 2 3 火车v(m/s) -5.0 -5.3 -5.6 -5.9 汽车v(m/s) -30 -25 -20 -15 计算结果:火车加速度是-0.3 m/s2,汽车加速度是5 m/s2。 这回汽车加速度变成正的了,但是汽车进站并没有因为我们正方向的选取改变,就变成减速运动了。同样,火车加速度为负,火车启动离站也没有因此就变成减速运动。 因此,我们得到这样一个认识:加速还是减速运动与加速度的正负没有关系! 那么,什么决定物体是加速还是减速运动? 看这样一个人的运动,从位置X1处经过一段时间来到位置X2处,如下图所示: (1)如果Vt大于V0,那么做的是加速运动。速度矢量图如下。 (2)如果Vt小于V0,那么做的是减速运动。速度矢量图如下。 仔细观察,我们能够得到这样的认识:物体是否做加速还是减速运动,判断依据是: 1:看速度绝对值的变化; 2:若a与速度方向相同,则是加速运动;若a与速度方向相反,则是减速运动。 【思考】一个直线运动的物体经过一段时间,速度变化如下矢量图所示。它做加速还是减速运动? 答案:先做减速运动,速度减为0后,速度反向,开始做加速运动。我们可以想象一下上抛粉笔,从开始抛出,到达最高点后,开始下落的这样一个运动过程。查看更多