- 2024-02-26 发布 |
- 37.5 KB |
- 7页

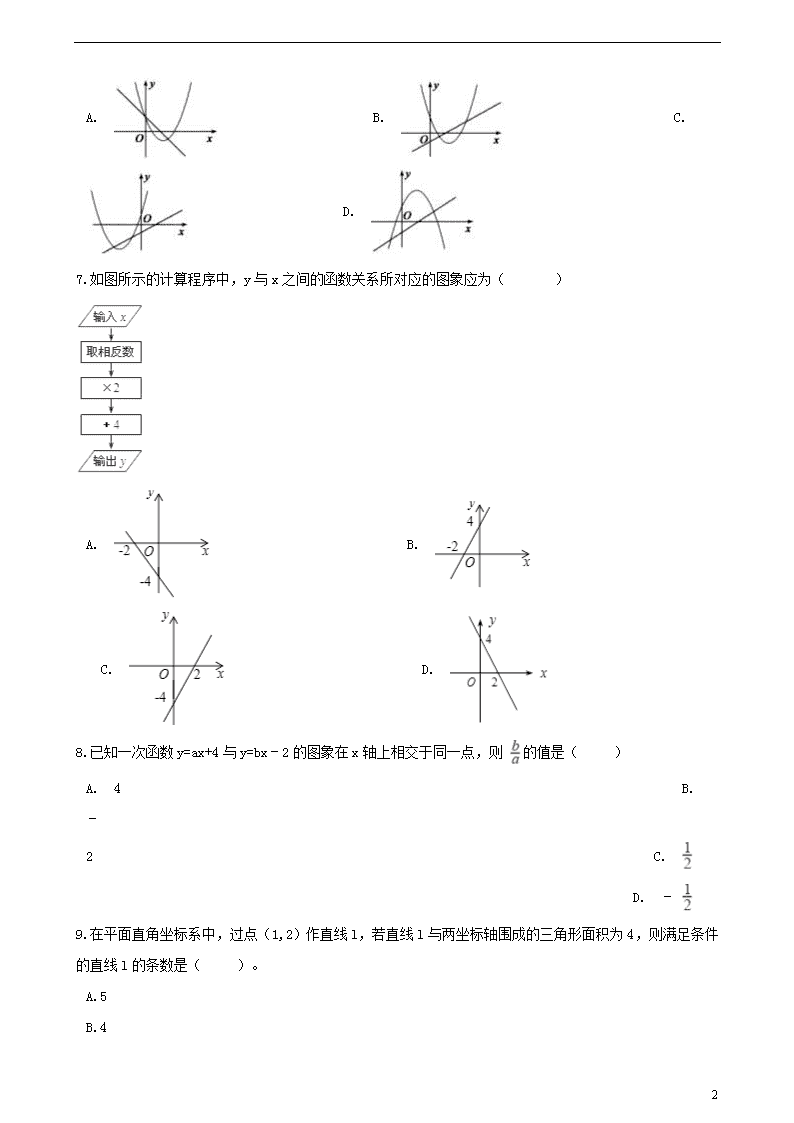

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年中考数学专题复习卷 一次函数(无答案)
一次函数 一、选择题 1.把函数y=x向上平移3个单位,下列在该平移后的直线上的点是( ) A. B. C. D. 2.给出下列函数:①y=﹣3x+2;②y= ;③y=2x2;④y=3x,上述函数中符合条作“当x>1时,函数值y随自变量x增大而增大“的是( ) A. ①③ B. ③④ C. ②④ D. ②③ 3.已知一次函数y=(k+1)x+b的图象与x轴负半轴相交,且函数值y随自变量x的增大而增大,则k,b的取值情况为( ) A. k>−1,b>0 B. k>−1,b<0 C. k<−1,b>0 D. k<−1,b<0 4.若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为( ) A. (-2,0) B. (2,0) C. (-6,0) D. (6,0) 5.已知函数y=kx+b的图象如图所示,则一元二次方程x2+x+2﹣k=0根的情况是( ) A. 没有实数根 B. 有两个相等的实数根 C. 有两个不相等的实数根 D. 无法确定 6.如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( ) 7 A. B. C. D. 7.如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( ) A. B. C. D. 8.已知一次函数y=ax+4与y=bx﹣2的图象在x轴上相交于同一点,则 的值是( ) A. 4 B. ﹣2 C. D. ﹣ 7 9.在平面直角坐标系中,过点(1,2)作直线l,若直线l与两坐标轴围成的三角形面积为4,则满足条件的直线l的条数是( )。 A.5 B.4 C.3 D.2 10.已知点A(x1 , y1)、B(x2 , y2)是直线y=- x+2上不同的两点,且x1<x2 , 若m=(x1-x2)(y1-y2)则( ) A. m=0 B. m<0 C. m>0 D. 不能比较 11.同一平面直角坐标系中,一次函数 的图像与正比例函数 的图像如图所示,则关于 的方程 的解为( ) A. B. C. D. 12.如图,直线l1:y=x+1与直线l2:y=﹣x﹣ 把平面直角坐标系分成四个部分,则点( , )在( ) A. 第一部分 B. 第二部分 C. 第三部分 D. 第四部分 7 二、填空题 13.将直线 向上平移2个单位长度,平移后直线的解析式为________. 14.若正比例函数 y =(k - 1)x 图象经过一、三象限,则 k 的取值范围是________. 15.某日上午,甲、乙两车先后从A地出发沿一条公路匀速前往B地,甲车8点出发,如图是其行驶路程s(千米)随行驶时间t(小时)变化的图象.乙车9点出发,若要在10点至11点之间(含10点和11点)追上甲车,则乙车的速度v(单位:千米/小时)的范围是________。 16.如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,﹣4),则四边形AOBC的面积为________. 17.(2017•大连)在平面直角坐标系xOy中,点A、B的坐标分别为(3,m)、(3,m+2),直线y=2x+b与线段AB有公共点,则b的取值范围为________(用含m的代数式表示). 18.(2017•海南)在平面直角坐标系中,已知一次函数y=x﹣1的图象经过P1(x1 , y1)、P2(x2 , y2)两点,若x1<x2 , 则y1________y2(填“>”,“<”或“=”) 19.(2017•达州)甲、乙两动点分别从线段AB的两端点同时出发,甲从点A出发,向终点B运动,乙从点B出发,向终点A运动.已知线段AB长为90cm,甲的速度为2.5cm/s.设运动时间为x(s),甲、乙两点之间的距离为y(cm),y与x的函数图象如图所示,则图中线段DE所表示的函数关系式为________.(并写出自变量取值范围) 7 20.(2017•十堰)如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx﹣6<ax+4<kx的解集为________. 三、解答题 21.甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案. 甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示. 乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元. (1)求如图所示的y与x的函数表达式; (2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算. 22.如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数 (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC 7 ,求反比例函数和一次函数的表达式. 23.为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图像(其中a, b,c为常数) 行驶路程 收费标准 调价前 调价后 不超过3km的部分 起步价6元 起步价a 元 超过3km不超出6km的部分 每公里2.1元 每公里b元 超出6km的部分 每公里c元 设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题: (1)填空:a=________,b=________,c=________. (2)写出当x>3时,y1与x的关系,并在上图中画出该函数的图象. 7 (3)函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由. 24.如图,在平面直角坐标系中,一次函数y=kx+b的图像经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图像交于点C,点C的横坐标为1. (1)求k、b的值; (2)若点D在y轴负半轴上,且满足S△COD= S△BOC , 求点D的坐标. 7查看更多