【40套试卷合集】河北省衡水市名校2019-2020学年数学九上期末模拟试卷含答案

【40套试卷合集】河北省衡水市名校2019-2020学年数学九上期末模拟试卷含答案

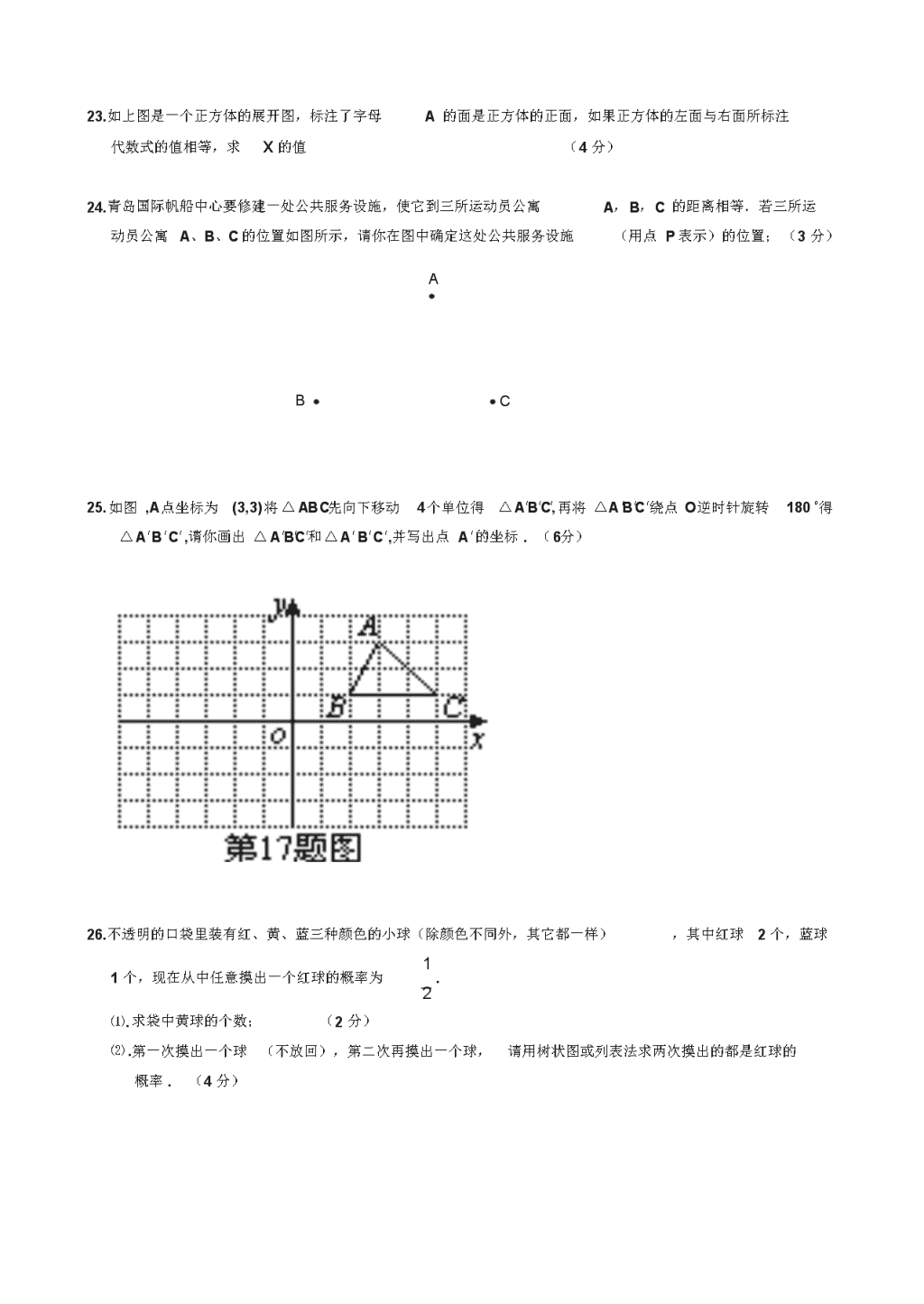
2 2019-2020 学年九上数学期末模拟试卷含答案 考号： 姓名： 分数： 友情提 示：计算时注意书写步骤，计算要认真！ 一.填空题 （每小题 3 分，共 45 分） 1. 当 x 时 ,式子 1 2 x 有意义。 x 1 2.当 x ≤ 0 时，化简 1 x x = 。 3. 比较大小： -2 3 -3 2 〔 填“＞、＝、＜” 〕 4.（2 48 －3 27 ）÷ 6 = ． 5.方程 3x2 6x 12 0 配方后的方程是 。 2 6.已知 2 - 5 是方程 x 4x c 0 的一个根， c = 。 7. 已知点 A（m,1）与点 B(3,n)关于原点对称，则 m+n= 。 8.下面图形：四边形，三角形，正方形，梯形，平行四边形，圆，从中任取一个图形既是轴对称图形又是 中心对称图形的概率为 。 9.在一个暗箱里放有 a 个除颜色外其它完全相同的球，这 a 个球中红球只有 3 个，每次将球搅拌均匀后， 任意摸出一个球记下颜色再放回暗箱 .通过大量反复试验后发现， 摸到红球的频率稳定在 25%，那么可以 推算出 a 大约是 个。 10.如图，一条公路的转弯处是一段圆弧（图中的 AB 弧），点 O 是这段弧的圆心， AB=120m，C是 AB 弧是 一点， OC⊥AB 于 D，CD=20m，则该弯路的半径为 。 11.如图， AC 是⊙ O 的直径，∠ ACB＝60°，连结 AB，过 A.B 两点分别作⊙ O 的切线，两 切线交于点 P，若已知⊙ O 的半径为 1，则△ PAB 的周长为 。 12.如图，等边三角形 ABC 的内切圆面积为 9π，则△ ABC 的周长为 。 A C D O B 13.如图，⊙ O 是△ ABC 的内切圆，切点分别是 D.E.F，∠ A=100°，∠ C=30°，则∠ DFE 的度数是 。 14.圆锥的母线长为 5cm，高为 3 cm，在它的侧面展开图中，扇形的圆心角是 。 15.如图，⊙ A、⊙ B、⊙ C、⊙ D 相互外离，它们的半径是 1，顺次连结四个圆心得到四边 形 ABCD，则图中四个扇形的面积和是 。 A D C B 2 2 二.选择题 （每小题 3 分，共 18 分） 16.下列二次根式中，与 5 3 是同类二次根式的是 （ ） A. 18 B. 0.3 C. 30 D. 300 17.关于 x 的一元二次方程 (m-2) 2 2 x +（2m+1）x+1=0 有两个实数根，则 m 取值范围是 （ ） 3 3 3 3 A. m B.m C.m 且 m 2 D.m 且 m 2 4 4 4 4 18.下列图形中，旋转 60 后可以和原图形重合的是 （ ） A.正六边形 B.正五边形 C.正方形 D.正三角形 19.下列各组图中，图形甲变成图形乙，既能用平移，又能用旋转的是 （ ） 甲 乙 甲 乙 甲 乙 甲 乙 A． B． C． D． 20.如图，王大爷家屋后有一块长 12m，宽 8m 的矩形空地，他在以 BC 为直径的半圆内种菜，他家养的一 只羊平时拴在 A 处，为了不让羊吃到菜，拴羊的绳长可以选用 （ ） A.3m B.5m C.7m D.9m 21.露露从纸上剪下一个圆形和一个扇形纸片（如图） ，用它们恰好能围成一个圆锥模型。若圆的半径为 1， 扇形的圆心角等于 120°，则此扇形的半径为 （ ） A． 3 B． 6 C．3 D．6 8m D C O 12m －2 3 x2 1 A P 第7 题 图 B A 3x-2 三.解答题（本大题共 8 小题，满分 57 分．解答应写出文字说明 .证明过程或演算步骤） 22.（8 分）计算： ( 31) ( 3 2) 2(3 1)(31) 23.计算： (5 48 6 27 4 15) 3 23.如上图是一个正方体的展开图，标注了字母 A 的面是正方体的正面，如果正方体的左面与右面所标注 代数式的值相等，求 x 的值 （4 分） 24.青岛国际帆船中心要修建一处公共服务设施，使它到三所运动员公寓 A，B，C 的距离相等．若三所运 动 员公寓 A、B、C 的位置如图所示，请你在图中确定这处公共服务设施 （用点 P 表示）的位置； （3 分） A B C 25.如图 ,A 点坐标为 (3,3)将 △ ABC先向下移动 4个单位得 △A′B′C′,再将 △A′B′C′绕点 O逆时针旋转 180°得 △A′B′C′,请′你画出 △ A′B′C′和△A′B′C′,并′写出点 A′的′坐标 . （6 分） 26.不透明的口袋里装有红、黄、蓝三种颜色的小球（除颜色不同外，其它都一样） ，其中红球 2 个，蓝球 1 1 个，现在从中任意摸出一个红球的概率为 . 2 ⑴. 求袋中黄球的个数； （2 分） ⑵ .第一次摸出一个球 （不放回），第二次再摸出一个球， 请用树状图或列表法求两次摸出的都是红球的 概率 . （4 分） 27.如图，正三角形 ABC 内接于⊙ O，若 AB=2 3 cm，求⊙ O 的周长 . （6 分） A . O B C 28.一个两位数，个位数字比十位数字大 3，个位数字的平方刚好等于这个两位数，则这个两位数是多少？ （8 分） 29.如图， AB是⊙ O 的直径，点 D 在⊙ O 上，∠ DAB＝ 45°， BC∥AD，CD∥AB． （ 1）判断直线 CD 与⊙ O 的位置关系，并说明理由； （ 6 分） （ 2）若⊙ O 的半径为 1，求图中阴影部分的面积（结果保留 π）． （10 分） D C A B O 温馨提示：恭喜你已经解答完所有问题，请再仔细检查一次，预祝你取得好成绩 2 2 2019-2020 学年九上数学期末模拟试卷含答案 （满分： 150 分 测试时间： 120 分钟） 一．选择题（每题有且 只有一个答案正确，请把你认为正确的答案前的字母填入下表相应的空格内，每题 3 分，计 24 分） 1．下列图形中，既是轴对称图形，又是中心对称图形的是（ ） A．平行四边形 B ．等边三角形 C ．等腰梯形 D ．正方形 2．如右图，数轴上点 N 表示的数可能是（ ） A． 2 B ． 3 C ． 5 D ． 10 3．给出下列四个结论，其中正确的结论为 ( ) N -1 0 1 2 3 4 图第3 2 题 A．等腰三角形底边上的中点到两腰的距离相等 B ．正多边形都是中心对称图形 C．三角形的外心到三条边的距离相等 D ．对角线互相垂直且相等的四边形是正方形 4．已知⊙O1、⊙O2 的半径 分别为 3cm、5cm，且它们的圆心距为 8cm，则⊙O1 与⊙O2 的位置关系是 （ ） A ．外切 B ．相交 C ．内切 D ．内含 (02 长沙市 ) 5．对任意实数 x ，多项式 x2 6x 10 的值是一个（ ） A. 正 数 B. 负数 C. 非负数 D. 无法确定 6．将抛物线 y x 2 1先向左平移 2 个单位，再向下平移 2 个单位，那么所得抛物线的函数关 系式是 （ ） A ． y＝ (x ＋ 2) 2 ＋2 B ．y＝ (x ＋2) 2 －2 C ．y＝ (x －2) 2 2 ＋2 D ．y＝ (x －2) －2 7．已知一元二次方程 为（ ） x 2 8x 15 0 的两个解 恰好分别是等腰△ ABC 的底边长和腰长，则△ ABC 的周长 A ．13 B ．11 C．11 或 13 D ．12 8．如图，二次函数 y=ax +bx+c（a≠0）的图象与 x 轴交于 A、B 两点，与 y 轴交于点 C，点 B 坐标（﹣ 1，0），下面 的四个结论：① OA=3；②a+b+c＜ 0；③ac＞ 0； ④b﹣4ac＞ 0．其中正确的结论是（ ） A．①④ B ．①③ C ．②④ D ．①② (02 长沙市 ) 二、填空题（本大题共 10 个小题，每小题 3 分，共 30 分．） 9．在函数关系式 y 1 中， x 的取值范围是 . x 1 10．已知梯形的中位线长是 4cm，下底长是 5cm，则它的上底长是 cm． 11．抛物线 y （x 1）2 2的顶点坐标是 ． 12．平面直角坐标系内的三个点 A（1， 0）、B（0，－ 3）、C（2，－ 3） 确定一个圆（填“能”或“不能” ）。 13．如图，在□ ABCD 中， AB＝6cm，∠BCD 的平分线交 AD 于点 E，则 DE＝ cm ． 14．已知一个圆锥的母线长为 10cm，将侧面展开后所得扇形的圆心角是 144°，则这个圆锥的底面圆的半 径是 cm ． 15． 二次函数 y x 2 6x n 的部分图像如图所示，若关于 x 的一元二次方程 x 2 6x n 0 的一个解为 x1 1 ，则另一个解 x 2 = ． 16．如图，⊙ O的直径 CD 过弦 EF 的中点 G，∠ EOG=60°，则∠ DCF等于 ． 17．如右图， AB 是⊙O的直径， C是 AB延长线上一点，且 BC＝ OB， CE 是⊙O 的切线， D为切点，过点 A 作 AE⊥CE，垂足为 E．则 CD∶DE 的值是 ． 18．如右图，连接在一起的两个正方 形的边长都为 1cm， 一个微型机器人由点 A 开始按 ABCDEFCGA 的顺序 沿正 方形 的边 循环移动．当微型机器人移动了 2013cm 时 ，它停在 点． 三、解答题（本大题共 10 个小题，共 96 分，解答时应写出文字说明、证明过程或演算步骤） 19．（本题满分 10 分）计算： （1） 8 6 27 2 （2） ( 0 1 1) ( 3) 1 3 20．（本题满分 10 分）解方程： （1） x 1 2 (1 x) 2 （2） 2x x 2 0 21．（本题满分 8 分）如图，在边长为 1 的小正方形组成的格中，△ AOB 的 三个顶点均在 格点 上，点 A、B 的坐标分别为 (3 ， 2) 、(1 ，3) ．△AOB 绕点 O 逆时针旋 转 90o 后得到△A1OB1． （1）在格中画出△A 1OB1，并标上字母； （2）点 A 关于 O 点中心对称的点的坐标为 ； （3）点 A1的坐标为 ； （4）在旋转过程中，点 B 经过的路径为弧 BB1，那么弧 BB1 的长为 ． 22．（本题满分 8 分）省射击队为从甲、乙两名运动员中选拔一人 参 加 全国比赛，对他们进 行了六次测试，测试成绩如下表（单位：环） ： 第一次 第二次 第三次 第四次 第五次 第六次 甲 10 8 9 8 10 9 乙 10 7 10 10 9 8 （ 1）根据表格中的数据，计算出甲的平均成绩是 环，乙的平均成绩是 环； （ 2）分别计算甲、乙六次测试成绩的方差； （ 3）根据（ 1）、（ 2）计算的结果，你认为推荐谁参加全国比赛更合适，请说明理由． 23．（本题满分 8 分）已知 a 2 与 b 1 是互为相反数，且一元二次方程 2 kx ax b 0 有两个不相 等实数根，求 k 的取值范围． 24．（本题满分 8 分）近年来，某区为发展教育事业，加大了对教育经费的投入， 2010 年投入 6000 万元， 2012 年投入 8640 万元． （ 1）求 2010 年至 2012 年该区投入教育经费的年平均增长率； （2）该区预计 2013 年 投入教育经费 9500 万元，问能否继续保持前两年的平均增长率？请通过计算说明 理由． 25. （本题满分 10 分）已知：如图， D 是△ABC 的边 AB 上一点， CN∥AB， DN 交 AC 于点 M，MA=M．C ①求证： CD=AN；②若∠ AMD=∠2 MCD，求证：四边形 ADCN是矩形． 26．（本题满分 10 分）．已知 AB 与⊙O 相切于点 C，且 OA=OB．OA、OB 与⊙O分别交于点 D、 E． (I) 如图①，若⊙O 的直径为 8， AB=10，求 OA 的长 ( 结果 保留根号 ) ； ( Ⅱ) 如图②，连接 CD、 CE，若四边形 ODCE为菱形．求 OD OA 的值． 27．（本题满分 12 分）某商店经营儿童益智玩具，已知成批购进时的单价是 20 元. 调查发现：销售单价是 30元时，月销售量是 230 件 ，而销 售单价每上涨 1 元，月销售量就减少 10 件，但每件玩具售价不能高于 40 元. 设每件玩具的销售单价上涨．．了 x 元时（ x．为．正．整．数． ），月销售利润为 y 元. （1）求 y 与 x 的函数关系式并直接写出自变量 x 的取值范围 . （2）每件玩具的售价．．定为多少元时，月销售利润恰为 2520 元？ （3）每件玩具的售价．．定为多少元时可使月销售利润最大？最大的 月利润是多少？ 28．（本题满分 12 分）如图，已知抛物线 2 y ax bx c 经过 A（4， 0），B（2， 3）， C（0， 3）三点． （1）求抛物线的解析式及对称轴． （ 2）在抛物线的对称轴上找一点 M，使得 MA+MB 的值最小，并求 出 点 M 的坐标． （3）在抛物线上是否存在一点 P，使得以点 A、B、C、P 四点为顶 点 所构成的四边形为梯形？若存在，请直接写 出点 P 的坐标；若不 存 在，请说明理由．