- 2024-02-02 发布 |
- 37.5 KB |
- 73页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习课件:8-8 立体几何中的向量方法
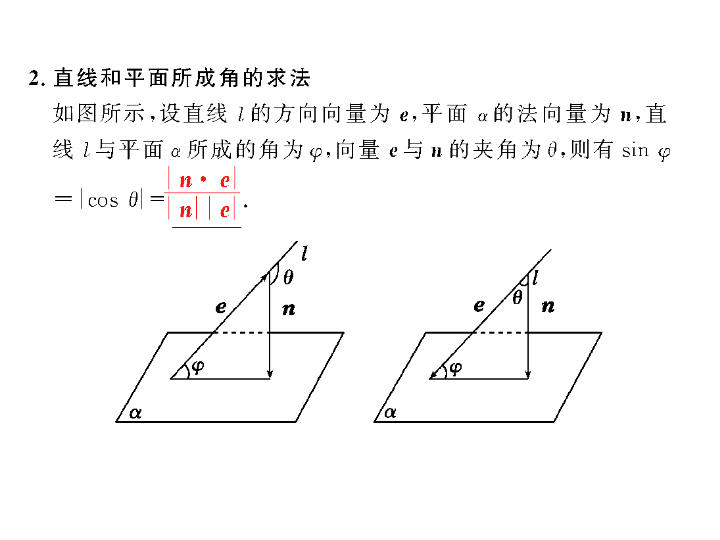
§8.8 立体几何中的向量方法 ( 二 )—— 求空间角和距离 [ 考纲要求 ] 能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题.了解向量方法在研究立体几何问题中的应用. 【 思考辨析 】 判断下面结论是否正确 ( 请在括号中打 “√” 或 “ ×” ) (1) 两直线的方向向量所成的角就是两条直线所成的角. ( ) (2) 直线的方向向量和平面的法向量所成的角就是直线与平面所成的角. ( ) (3) 两个平面的法向量所成的角是这两个平面所成的角. ( ) 【 答案 】 (1) × (2) × (3) × (4) √ (5) √ (6) × 1 .如图,在正方体 ABCD A 1 B 1 C 1 D 1 中, M , N 分别是棱 CD , CC 1 的中点,则异面直线 A 1 M 与 DN 所成的角的大小是 ( ) A . 30 ° B . 45 ° C . 60 ° D . 90 ° 【 答案 】 D 【 答案 】 A 3 . ( 教材改编 ) 正三棱柱 ( 底面是正三角形的直棱 柱 ) ABC A 1 B 1 C 1 的底面边长为 2 ,侧棱长为 2 ,则 AC 1 与侧面 ABB 1 A 1 所成的角为 ________ . 【 答案 】 60 ° 5 . P 是二面角 α AB β 棱上的一点,分别在平面 α , β 上引射线 PM , PN ,如果 ∠ BPM = ∠ BPN = 45 ° , ∠ MPN = 60 ° ,那么二面角 α AB β 的大小为 ________ . 【 答案 】 90° 题型一 求异面直线所成的角 【 例 1 】 (2015· 四川 ) 如图,四边形 ABCD 和 ADPQ 均为正方形,它们所在的平面互相垂直,动点 M 在线段 PQ 上, E , F 分别为 AB , BC 的中点.设异面直线 EM 与 AF 所成的角为 θ ,则 cos θ 的最大值为 ________ . 【 解析 】 建立空间直角坐标系如图所示, 【 方法规律 】 用向量法求异面直线所成角的一般步骤: (1) 选择三条两两垂直的直线建立空间直角坐标系; (2) 确定异面直线上两个点的坐标,从而确定异面直线的方向向量; (3) 利用向量的夹角公式求出向量夹角的余弦值; (4) 两异面直线所成角的余弦等于两向量夹角余弦值的绝对值. 跟踪训练 1 如右图所示正方体 ABCD A ′ B ′ C ′ D ′ ,已知点 H 在 A ′ B ′ C ′ D ′ 的对角线 B ′ D ′ 上, ∠ HDA = 60 ° . 求 DH 与 CC ′ 所成的角的大小. 题型二 求直线与平面所成的角 【 例 2 】 (2017· 郑州模拟 ) 如图,在三棱柱 ABC A 1 B 1 C 1 中,四边形 AA 1 C 1 C 是边长为 2 的菱形,平面 ABC ⊥ 平面 AA 1 C 1 C , ∠ A 1 AC = 60 ° , ∠ BCA = 90 ° . (1) 求证: A 1 B ⊥ AC 1 ; (2) 已知点 E 是 AB 的中点, BC = AC ,求直线 EC 1 与平面 ABB 1 A 1 所成的角的正弦值. 【 解析 】 (1) 证明 取 AC 的中点 O ,连接 A 1 O , 因为四边形 AA 1 C 1 C 是菱形,且 ∠ A 1 AC = 60 ° ,所以 △ A 1 AC 为等边三角形,所以 A 1 O ⊥ AC , 又平面 ABC ⊥ 平面 AA 1 C 1 C , 所以 A 1 O ⊥ 平面 ABC , 所以 A 1 O ⊥ BC . 又 BC ⊥ AC , 所以 BC ⊥ 平面 AA 1 C 1 C , 所以 AC 1 ⊥ BC . 在菱形 AA 1 C 1 C 中, AC 1 ⊥ A 1 C , 所以 AC 1 ⊥ 平面 A 1 BC , 所以 A 1 B ⊥ AC 1 . 【 方法规律 】 利用向量法求线面角的方法: (1) 分别求出斜线和它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角 ( 或其补角 ) ; (2) 通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线和平面所成的角. 跟踪训练 2 (2016· 课标全国 Ⅲ ) 如图,在四棱锥 P ABCD 中, PA ⊥ 底面 ABCD , AD ∥ BC , AB = AD = AC = 3 , PA = BC = 4 , M 为线段 AD 上一点, AM = 2 MD , N 为 PC 的中点. 【 方法规律 】 求二面角最常用的方法就是分别求出二面角的两个半平面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角是锐角还是钝角. 跟踪训练 3 (2017· 浙江台州中学模拟 ) 三棱锥 P ABC 中, PA ⊥ 平面 ABC , AB ⊥ BC . 【 解析 】 (1) 证明 ∵ PA ⊥ 平面 ABC , ∴ PA ⊥ BC . ∵ AB ⊥ BC ,且 PA ∩ AB = A , ∴ BC ⊥ 平面 PAB . 而 BC ⊂ 平面 PBC , ∴ 平面 PAB ⊥ 平面 PBC . (2) 方法一 过 A 作 AE ⊥ PB 于 E ,过 E 作 EF ⊥ PC 于 F ,连接 AF ,如图所示,则 ∠ EFA 为 B PC A 的二面角的平面角. (1) 证明:平面 MBD ⊥ 平面 PAD ; (2) 若 PA 与平面 PBD 成 60 ° 角,当平面 MBD ⊥ 平面 ABCD 时,求点 M 到平面 ABCD 的距离. 【 解析 】 (1) 证明 因为 BD = 2 AD = 8 , AB = 4 ,由勾股定理得 BD ⊥ AD . 因为平面 PAD ⊥ 平面 ABCD ,平面 PAD ∩ 平面 ABCD = AD , BD ⊂ 平面 ABCD ,所以 BD ⊥ 平面 PAD . 因为 BD ⊂ 平面 MBD ,所以平面 MBD ⊥ 平面 PAD . 【 方法规律 】 求点面距一般有以下三种方法: ① 作点到面的垂线,点到垂足的距离即为点到平面的距离; ② 等体积法; ③ 向量法.其中向量法在易建立空间直角坐标系的规则图形中较简便. 【 解析 】 如图,过 P 作 PO ⊥ 平面 ABCD ,垂足为 O ,以 O 为原点,过 O 作 DA 的平行线为 x 轴,过 O 作 AB 的平行线为 y 轴, OP 为 z 轴,建立空间直角坐标系,如图所示. 【 答案 】 C 答题模板系列 6 利用空间向量求解空间角 【 典例 】 (12 分 )(2017· 河南郑州质检 ) 如图,在四棱锥 P ABCD 中, PA ⊥ 底面 ABCD , AD ⊥ AB , AB ∥ DC , AD = DC = AP = 2 , AB = 1 ,点 E 为棱 PC 的中点. (1) 证明: BE ⊥ DC ; (2) 求直线 BE 与平面 PBD 所成角的正弦值; (3) 若 F 为棱 PC 上一点,满足 BF ⊥ AC ,求二面角 F AB P 的余弦值. 【 规范解答 】 (1) 证明 依题意,以点 A 为原点建立空间直角坐标系如图,可得 B (1 , 0 , 0) , C (2 , 2 , 0) , D (0 , 2 , 0) , P (0 , 0 , 2) . (1 分 ) 由 E 为棱 PC 的中点,得 E (1 , 1 , 1) . 【 答题模板 】 利用向量求空间角的步骤 第一步:建立空间直角坐标系. 第二步:确定点的坐标. 第三步:求向量 ( 直线的方向向量、平面的法向量 ) 坐标. 第四步:计算向量的夹角 ( 或函数值 ) . 第五步:将向量夹角转化为所求的空间角. 第六步:反思回顾.查看关键点、易错点和答题规范. 【 温馨提醒 】 (1) 利用向量求角是高考的热点,几乎每年必考,主要是突出向量的工具性作用. (2) 本题易错点是在建立坐标系时不能明确指出坐标原点和坐标轴,导致建系不规范. (3) 将向量的夹角转化成空间角时,要注意根据角的概念和图形特征进行转化,否则易失分 . ► 方法与技巧 1 .用向量来求空间角,都需将各类角转化成对应向量的夹角来计算,问题的关键在于确定对应线段的向量. 2 .求点到平面的距离,若用向量知识,则离不开以该点为端点的平面的斜线段. ► 失误与防范 1 .利用向量求角,一定要注意将向量夹角转化为各空间角.因为向量夹角与各空间角的定义、范围不同. 2 .求点到平面的距离,有时利用等体积法求解可能更方便. 3 .求二面角要根据图形确定所求角是锐角还是钝角 .查看更多