- 2024-01-26 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
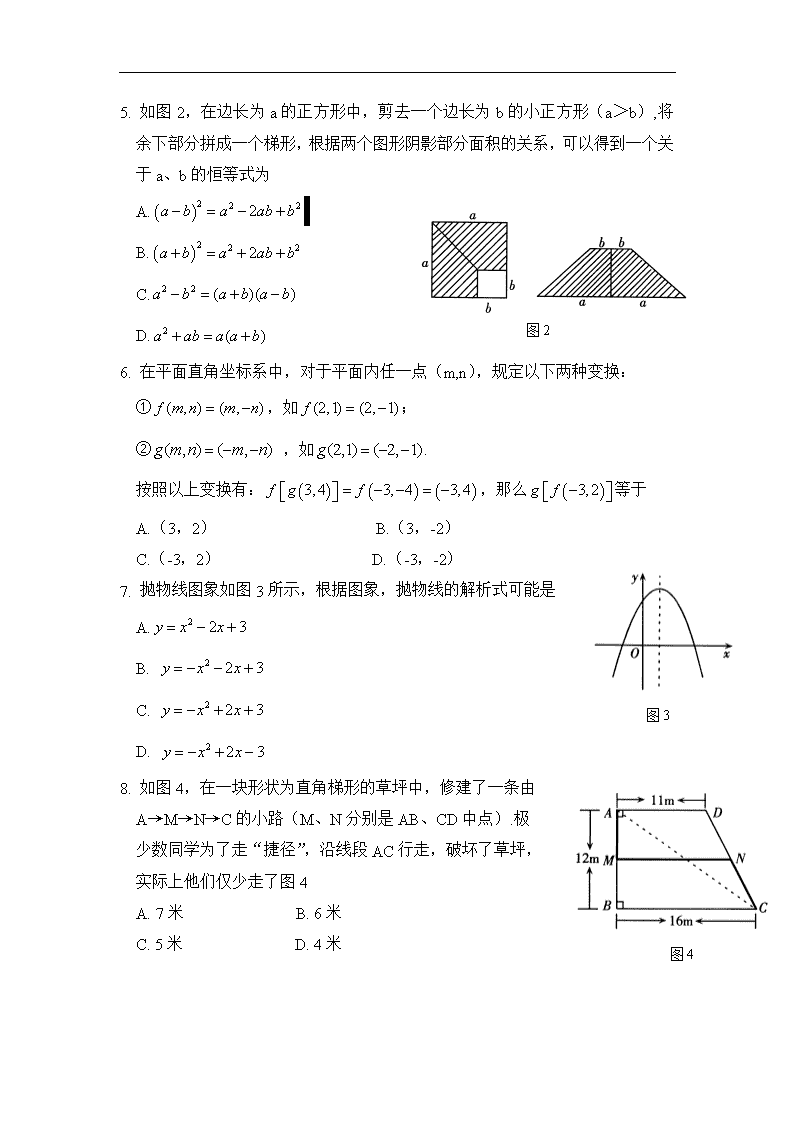
达州市2010年高中阶段教育学校招生统一考试数学
达州市2010年高中阶段教育学校招生统一考试 数学 本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至10页.考试时间100分钟,满分100分. 第Ⅰ卷(选择题共24分) 1.答第Ⅰ卷前,考生务必将姓名、准考证号、考试科目按要求填涂在答题卡上. 2.每小题选出答案后,用铅笔把答题卡上对应题号的答案标号涂黑,不能将答案答在试题卷上. 3.考试结束,将本试卷和答题卡一并交回. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本题8小题,每小题3分,共24分). 图1 1. 生活处处皆学问.如图1,自行车轮所在两圆的位置关系是 A. 外切 B. 内切 C. 外离 D. 内含 2. 4的算术平方根是 A. 2 B. ±2 C. -2 D. 3. 下列几何体中,正视图、左视图、俯视图完全相同的是 A. 圆柱 B. 圆锥 C. 棱锥 D. 球 4. 函数中自变量的取值范围在数轴上表示为 5. 如图2,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为 图2 A. B. C. D. 6. 在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换: ①,如; ② ,如. 按照以上变换有:,那么等于 A.(3,2) B.(3,-2) 图3 C.(-3,2) D.(-3,-2) 7. 抛物线图象如图3所示,根据图象,抛物线的解析式可能是 A. B. C. D. 图4 8. 如图4,在一块形状为直角梯形的草坪中,修建了一条由 A→M→N→C的小路(M、N分别是AB、CD中点).极 少数同学为了走“捷径”,沿线段AC行走,破坏了草坪, 实际上他们仅少走了图4 A. 7米 B. 6米 C. 5米 D. 4米 达州市2010年高中阶段教育学校招生统一考试数学 注意事项: 1.用蓝黑色钢笔或圆珠笔直接答在试题卷上. 2.答卷前将密封线内各项目填写清楚. 得分 评卷人 第Ⅱ卷(非选择题共76分) 二、填空题:把最后答案直接填在题中的横线上(本题7小题,每小题3分,共21分). 9. 0的相反数是 . 10. 大巴山隧道是达陕高速公路中最长的隧道,总长约为6000米,这个数据用科学记数法表示为 米. 11. 在“讲政策、讲法制、讲道德、讲恩情”的演讲比赛中,五位选手的成绩 如下: 选手编号 1 2 3 4 5 成绩(分) 85 92 90 95 88 图5 这组成绩的极差是 分. 12. 如图5,一水库迎水坡AB的坡度︰, 则该坡的坡角= . 13. 请写出符合以下两个条件的一个函数解析式 . 图6 ①过点(-2,1), ②在第二象限内,y随x增大而增大. 14. 如图6,一个宽为2 cm的刻度尺在圆形光盘上移动,当刻 度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的 读数恰好是“2”和“10”(单位:cm),那么该光盘的 直径是 cm. 图7 15. 如图7,△ABC中,CD⊥AB,垂足为D.下列条件中,能证明△ABC是直角三角形的有 (多选、错选不得分). ①∠A+∠B=90° ② ③ ④ 三、解答题:解答时应写出必要的文字说明、证明过程或演算步骤(共55分). 得分 评卷人 (一)(本题2小题,共15分) 16.(8分) (1)(4分)计算:. (2)(4分)对于代数式和,你能找到一个合适的值,使它们的值相等吗?写出你的解题过程. 17.(7分)上海世博会自开幕以来,前往参观的人络绎不绝.柳柳于星期六去参观,她决定上午在三个热门馆:中国馆(A),阿联酋馆(B),英国馆(C)中选择一个参观,下午在两个热门馆:瑞士馆(D)、非洲联合馆(E)中选择一个参观.请你用画树状图或列表的方法,求出柳柳这一天选中中国馆(A)和非洲联合馆(E)参观的概率是多大?(用字母代替馆名) 得分 评卷人 (二)(本题2小题,共11分) 18.(5分)如图8,将一矩形纸片ABCD折叠,使点C与点A重合,点D落在点E处,折痕为MN,图中有全等三角形吗?若有,请找出并证明. 图8 19.(6分)在一块长16m,宽12m的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案. (1)同学们都认为小华的方案是正确的,但对小芳方案是否符合条件有不同意见,你认为小芳的方案符合条件吗?若不符合,请用方程的方法说明理由. (2)你还有其他的设计方案吗?请在图9-3中画出你所设计的草图,将花园部分涂上阴影,并加以说明. 得分 评卷人 (三)(本题2小题,共14分) 20.(6分)已知:如图10,AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻,AB在阳光下的投影BC=4 m. (1)请你在图中画出此时DE在阳光下的投影,并简述画图步骤; (2)在测量AB的投影长时,同时测出DE在阳光下的投影长为6 m,请你计算DE的长. 图10 21.(8分)近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4 mg/L,此后浓度呈直线型增加,在第7小时达到最高值46 mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图11,根据题中相关信息回答下列问题: (1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围; (2)当空气中的CO浓度达到34 mg/L时,井下3 km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生? (3)矿工只有在空气中的CO浓度降到4 mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井? 图11 得分 评卷人 (四)(本题2小题,共15分) 22.(6分)已知:如图12,在锐角∠MAN的边AN上取一点B,以AB为直径的半圆O交AM于C,交∠MAN的角平分线于E,过点E作ED⊥AM,垂足为D,反向延长ED交AN于F. (1)猜想ED与⊙O的位置关系,并说明理由; (2)若cos∠MAN=,AE=,求阴影部分的面积. 图12 23.(9分)如图13,对称轴为的抛物线与轴相交于点、. (1)求抛物线的解析式,并求出顶点的坐标; (2)连结AB,把AB所在的直线平移,使它经过原点O,得到直线l.点P是l上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为,当0<S≤18时,求的取值范围; (3)在(2)的条件下,当取最大值时,抛物线上是否存在点,使△OP为直角三角形且OP为直角边.若存在,直接写出点的坐标;若不存在,说明理由. 图13 达州市2010年高中阶段教育学校招生统一考试 数学参考答案及评分意见 说明:1.本解答仅供参考,如果考生的解法与本解答不同,请根据解答情况参考评分意见给分. 2.对解答题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分. 3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 一、选择题(本题8小题. 每小题3分,共24分) 1. C 2. A 3. D 4. D 5. C 6. A 7. C 8. B 二、填空题(本题7小题. 每小题3分,共21分) 9. 0 10. 11. 10 12. 30° 13. y=-2x,y=x+3,y=-x2+5等 14. 10 15. ①②④(选对一个得1分,多选、错选不得分) 三、解答题(共55分) (一)(本题2小题,共15分) 16.(1)解: 原式=1-1 ………………………………3分 =0. ………………………………4分 (2)解:能. ………………………………0.5分 根据题意,设= ,………………………………1分 则有2x+1=3(x-2). ………………………………2分 解得:x=7, ………………………………3分 经检验得x=7是=的解. 所以,当x=7时,代数式和 的值相等. ……………4分 (说明:不检验扣1分) 17.解: ………………………………5分 由上可知,共有6种等可能情况,其中选中A和E的情况只有1种,所以,选中中国馆(A)和非洲联合馆(E)参观的概率P=. ……………………7分(二)(本题2小题,共11分) 18.解:有,△ABN≌△AEM. ………………………………1分 证明:∵四边形ABCD是矩形, ∴AB=DC,∠B=∠C=∠DAB=90°. ………………………………2分 ∵四边形NCDM翻折得到四边形NAEM, ∴AE=CD,∠E=∠D=90°,∠EAN=∠C=90°……………………………….3分 ∴AB=AE,∠B=∠E, ∠DAB=∠EAN, 即:∠BAN+∠NAM=∠EAM+∠NAM, ∴∠BAN=∠EAM. ………………………………4分 在△ABN与△AEM中, ∴△ABN≌△AEM. ………………………………5分 19.解:(1)不符合. ………………………………1分 设小路宽度均为 m,根据题意得: ,………………………………2分 解这个方程得: 但不符合题意,应舍去,∴.………………………………3分 ∴小芳的方案不符合条件,小路的宽度均为2m. ……………………4分 (2)答案不唯一.6分 例如: (三)(本题2小题,共14分) 20.解:(1) 作法:连结AC,过点D作DF∥AC,交直线BE于F, 则EF就是DE的投影.(画图1分,作法1分). ………………………2分 (2)∵太阳光线是平行的, ∴AC∥DF. ∴∠ACB=∠DFE. 又∵∠ABC=∠DEF=90°, ∴△ABC∽△DEF. ………………………………4分 ∴, ∵AB=5m,BC=4m,EF=6m, ∴, ∴DE=7.5(m). ………………………………6分 21.解:(1)因为爆炸前浓度呈直线型增加, 所以可设y与x的函数关系式为 由图象知过点(0,4)与(7,46) ∴. 解得, ∴,此时自变量的取值范围是0≤≤7. (不取=0不扣分,=7可放在第二段函数中) …………………………2分 因为爆炸后浓度成反比例下降, 所以可设y与x的函数关系式为. 由图象知过点(7,46), ∴. ∴, ∴,此时自变量的取值范围是>7. …………………………4分 (2)当=34时,由得,6+4=34,=5 . ∴撤离的最长时间为7-5=2(小时). ∴撤离的最小速度为3÷2=1.5(km/h). …………………………6分 (3)当=4时,由得, =80.5,80.5-7=73.5(小时). ∴矿工至少在爆炸后73.5小时能才下井. …………………………8分 (四)(本题2小题,共15分) 22.证明:(1)DE与⊙O相切. …………………………1分 理由如下: 连结OE. ∵AE平分∠MAN, ∴∠1=∠2. ∵OA=OE, ∴∠2=∠3. ∴∠1=∠3, ∴OE∥AD. ∴∠OEF=∠ADF=90°,…………………………2分 即OE⊥DE,垂足为E. 又∵点E在半圆O上, ∴ED与⊙O相切. …………………………3分 (2)∵cos∠MAN=, ∴∠MAN=60°. ∴∠2=∠MAN=×60°=30°, ∠AFD=90°-∠MAN=90°-60°=30°. ∴∠2=∠AFD, ∴EF=AE=. …………………………4分 在Rt△OEF中,tan∠OFE=, ∴tan30°=, ∴OE=1. …………………………5分 ∵∠4=∠MAN=60°, ∴S阴= =.…………………………6分 23.解:(1)∵点B与O(0,0)关于x=3对称, ∴点B坐标为(6,0). 将点B坐标代入得: 36+12=0, ∴=. ∴抛物线解析式为.…………………………2分 当=3时,, ∴顶点A坐标为(3,3). …………………………3分 (说明:可用对称轴为,求值,用顶点式求顶点A坐标.) (2)设直线AB解析式为y=kx+b. ∵A(3,3),B(6,0), ∴ 解得, ∴. ∵直线∥AB且过点O, ∴直线解析式为. ∵点是上一动点且横坐标为, ∴点坐标为().…………………………4分 当在第四象限时(t>0), =12×6×3+×6× =9+3. ∵0<S≤18, ∴0<9+3≤18, ∴-3<≤3. 又>0, ∴0<≤3.5分 当在第二象限时(<0), 作PM⊥轴于M,设对称轴与轴交点为N. 则 =-3+9. ∵0<S≤18, ∴0<-3+9≤18, ∴-3≤<3. 又<0, ∴-3≤<0.6分 ∴t的取值范围是-3≤<0或0<≤3. (3)存在,点坐标为(3,3)或(6,0)或(-3,-9).9分 (说明:点Q坐标答对一个给1分)查看更多